Преобразование восьмеричных чисел

Преобразование восьмеричных чисел в десятичные происходит по тому же принципу, как и преобразование шестнадцатеричных чисел в десятичные (разд. 8.5.2).

Алгоритм преобразования десятичного числа в восьмеричное аналоги­чен рассмотренному в разд. 8.5.3. Только основание степени другое.

Пример——————————————————————————————

Десятичное число 1983 нужно преобразовывать в восьмеричное число. Пред­лагается использовать таблицу согласно рис. 8.26. В столбце 8³ может сто­ять восьмеричная цифра 3, так как 3 • 512 равно 1536. Восьмеричная цифра 3 в столбце 8³ имеет значение 1536. Остается еще остаток 447.

В столбце 8² может стоять восьмеричная цифра 6, так как 6 • 64 равно 384. Такое значение имеет восьмеричная цифра 6 в этом столбце. Остается еще 63:

Для столбца 8¹ получается восьмеричная цифра 7. Она представляет зна­чение 7 • 8 = 56. Вычитая из 63 число 56, получаем остаток 7. В столбец 8° записывается восьмеричная цифра 7, так как 7 • 1 равно 7:

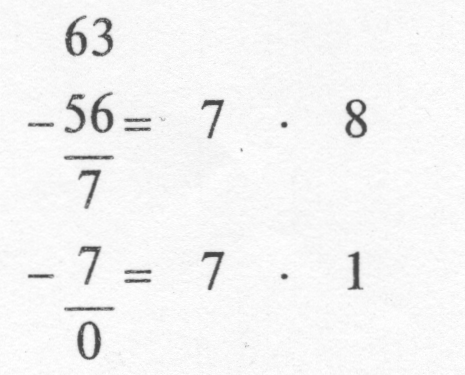
Результат преобразования:

1983₍₁₀₎ = 3677₍₈₎

Как и для шестнадцатеричной системы, между двоичной и восьмерич­ной системами счисления имеется тесная связь. Все числа с основанием 8 также могут быть записаны как числа с основанием 2 (8° = 2°, 8^і = 2³, 8² = 2^б и т. д.). Если составить уже известную таблицу пересчета для двоичных чисел, то окажется, что содержимое каждого третьего столбца в двоичной системе соответствует по величине содержимому столбца восьмеричной системы (рис. 8.27).

Любое трехразрядное двоичное число может быть представлено одним восьмеричным числом.

С одним трехразрядным числом можно вести счет от 0 до 7, значит, всего существуют 8 триад (троек бинарных разрядов). Каждая триада соот­ветствует восьмеричной цифре (рис. 8.28).

Двоичные числа с разрядностью больше чем три представляются не­сколькими восьмеричными цифрами, каждая из которых представляет три двоичных разряда. Если последняя группа слева содержит меньше, чем три разряда, то ее нужно дополнить нулями до трех разрядов.

Группа из трех двоичных цифр представляет одно восьмеричное число.

Пример——————————————————————————————

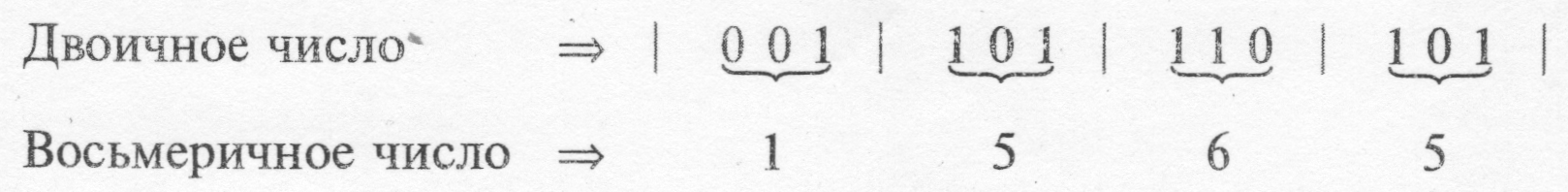
Итак, преобразовывать двоичные числа в восьмеричные очень легко.

Если нужно преобразовать двоичное число в восьмеричное, то для каж­дой восьмеричной цифры записывают соответствующие три двоичных раз­ряда.

Каждая восьмеричная цифра представляется тремя двоичными разрядами.

Пример——————————————————————————————

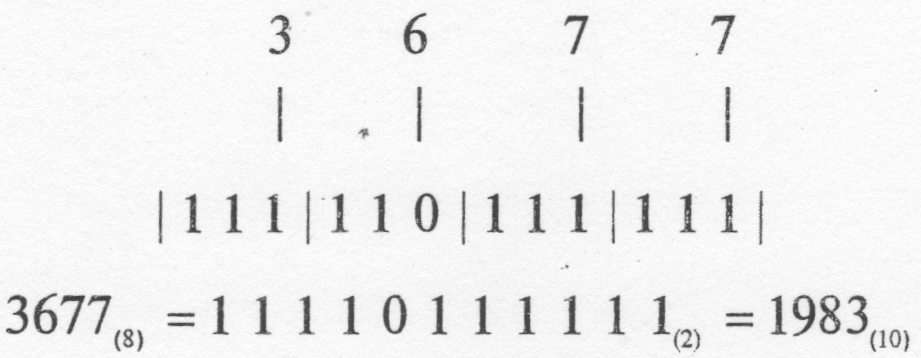
Согласно рис. 8.26 является 3677₍₈₎ = 1983₍₁₀₎

Если нужно преобразовать восьмеричное число в шестнадцатеричное, то это очень удобно сделать через двоичную систему счисления. Восьмеричное число расписывается как двоичное, группируется по тетрадам, и затем каж­дая тетрада заменяется соответствующей шестнадцатеричной цифрой.

Пример——————————————————————————————

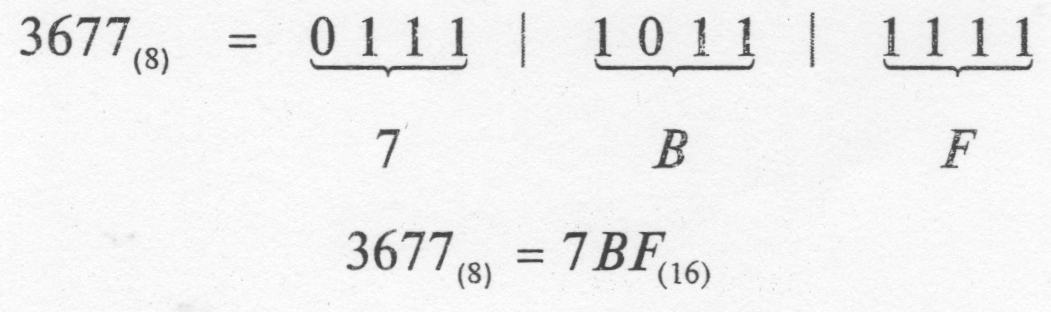
Коды, распознающие ошибки

Понятие избыточности

Распознавание ошибок возможно только при наличии дополнительной из­быточной информации, то есть передаваемая информация превышает не­обходимый минимум. Если оратор очень кратко о чем-то рассказывает, то часто по его речи нельзя оценить правильность высказывания. Если же оратор во время выступления дает дополнительные сведения, то возможна проверка правильности сказанного. Такая дополнительная информация на­зывается избыточной (redundans, лат. — в изобилии).

Наш язык и письменность содержат довольно большую избыточность. Только благодаря избыточности можно идентифицировать орфографичес­кие ошибки и опечатки. Это становится ясно, если мы рассмотрим пример информации без избыточности. Цифра 7 представляется в двоично-деся- тичном коде как 0111. Если в процессе передачи данных 1 ошибочно пере­дастся как 0, то получится 0101. Это уже цифра 5. Без дополнительной информации мы не узнаем, что полученная 5 ошибочна.

Если цифра 7 будет передаваться в словесной форме как «семь» и в процессе передачи будет изменена одна буква, то ошибка будет сразу оче­видна (например, «семв» вместо «семь»). Словесная форма содержит до­полнительную информацию, избыточность.

Избыточность существует всегда в том случае, если кроме собственно ин формации передаются дополнительные сведения, которые помогают при узнавании или исправлении ошибки.

Чтобы определить наличие ошибки, во многих случаях хватает незначи­тельной избыточности. Если ошибка должна быть не только идентифици­рована, но и исправлена, требуется больше дополнительных сведений — большая избыточность.

Для исправления ошибок необходима большая избыточность, чем только для их идентификации.

Потребность в идентификации ошибок и их исправлении привела к появлению специализированных кодов.