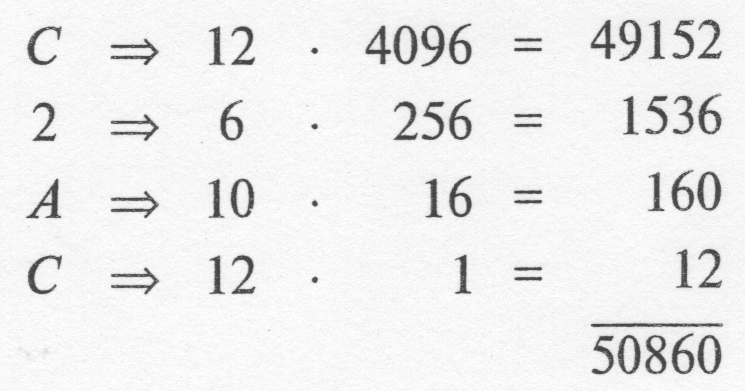Код Айкена

В коде Айкена используются первые и последние пять из 16 возможных тетрад. Псевдотетрады находятся в середине (рис. 8.12). Получается сим­метричный код, в котором легко получить дополнение до 9.

Дополнение до 9 К(9) получается в коде Айке­на простым инвертированием.

Для отдельных позиции в пределах тетрады действуют следующие соотношения:

D	С	В	А
2	4	2	1

Каждая десятичная цифра выражается тетрадой.

Пример——————————————————————————————

При сложении коррекция требуется только тогда, когда образуется псев­дотетрада. Действуют следующие правила.

Если при сложении двух тетрад в коде Айкена возникает псевдотетрада переносом в 5-й разряд, то от результата следует отнять число 0110.

Если при сложении двух тетрад в коде Айкена возникает псевдотетрада без переноса в 5-й разряд, то к результату следует прибавить число 0110.

Пример——————————————————————————————

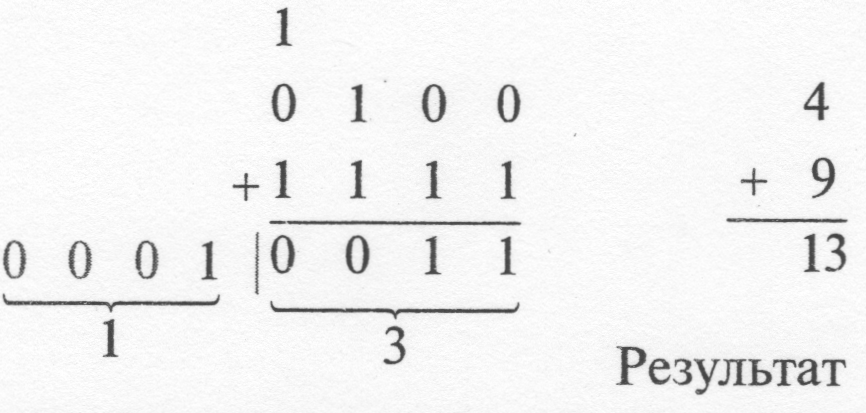
Так как не образуется псевдотетрада, то коррекция не нужна.

Пример——————————————————————————————

0	1	0	0
+ 0	0	1	1
0	1	1	1

4

+ 3

7

Псевдотетрада: (без переноса в 5-ом разряде)

0	1	1	1
+ 0	1	1	0
1	1	0	1

Коррекция

= 7 (Результат)

Пример——————————————————————————————

1	1	1
1	0	1	1
+1	1	0	1
1	0	0	0

5

+ 7

12

Псевдотетрада: (с переносом в 5-ом разряде)

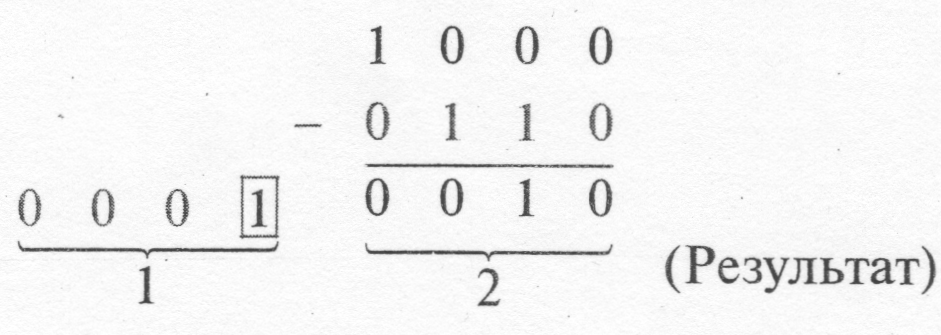
Код Грея

Код Грея не разрабатывался с точки зрения удобства для кодирования. Его особенностью является то, что при переходе от тетрады к тетраде всегда только один разряд меняется с 0 на 1 или от 1 на 0. То есть изменяется всегда только один бит тетрады (рис. 8.13).

Коды, в которых при переходе от одной тетрады к следующей всегда меня ется только один бит, называются одношаговыми. Код Грея является одноша говым кодом.

Одношаговые коды также называют прогрессивными кодами. ВСО-код, код с избытком 3 и код Айкена являются, напротив, многошаговыми кода­ми. В многошаговом коде при переходе от одной тетрады к следующей может появиться ошибка, если все биты, которые должны измениться, из­меняются не одновременно. Если, например, изменился один бит, а два других бита еще нет, то вплоть до изменения других битов в наличии име­ется ошибочная тетрада.

Код Грея используется прежде всего для задач управления и особенно часто — при считывании кодирующих дисков. При таком считывании нельзя обеспечить, чтобы изменение сигнала происходило одновременно по всем битам. Многошаговые коды для решения подобных задач проблематичны.

Представленный на рис. 8.13 код Грея имеет недостаток: при переходе от 9₍₁₀₎ = 1101 к 0₍₁₀₎ = 0000 должны изменяться три бинарных разряда. Гово­рят, код Грея не является циклическим.

Код Грея может расширяться на все 16 возможных тетрад (рис. 8.14). При расширенном коде Грея отдельные тетрады следуют в такой последо­вательности, что при переходе от 15 на 0 также изменяется только один бит. Расширенный код Грея является циклическим.

Прикладной областью применения кода Грея является кодирование угла. Каждой величине угла ставится в соот­ветствие определенная тетрада кода Грея. Чаще всего используется расширенный код Грея.

На рис. 8.15 изображен поворотный кодирующий диск. Шестнадцать тетрад расширенного кода Грея поделены на 90°.

Сегменты выдают 1-сигнал.

Кодирующий диск считывается электрически четырьмя щетками. Диск прикреплен к валу и вращается под фиксированными щетками. Примерно каждые 6° на четырех щетках оказывается следующая тетрада. Более тонкое разрешение получают, если 16 тетрадам ставится в соответствие 16 знако­вых градусов. Однозначное кодирование возможно в этом случае только в угловом диапазоне от 0 до 15°.

Шестнадцатеричная система счисления (Hexadecimal)

Структура шестнадцатеричной системы счисления

Шестнадцатеричная система является позиционной системой счисления. В качестве основания используются степени числа 16.

Шестнадцатеричная система является позиционной системой счисления. В качестве основания используются степени числа 16.

Структура шестнадцатеричной системы счисления показана на рис. 8.16. В разряде, которому поставлена в соответствие 16° = 1, можно считать до 15. Только начиная с 16 можно задействовать второй разряд. Итак, вместе с нулем э каждом разряде задействованы 16 цифр.

В шестнадцатеричной системе счисления задействованы 16 цифр.

Прежде всего применяются известные 10 цифр десятичной системы от 0 до 9.

Для цифр от 10 до 15 можно было бы придумать какие-нибудь новые цифры. Но их не было бы на пишущих машинках и в типографиях. Поэтому вме­сто шестнадцатеричных цифр используют буквы А, В, С, D, Е и F(рис. 8.17). Двойная функция буквы и цифры не приводит к путанице. Из контекста мож­но понять, обычная ли это буква или буква, выпол­няющая функцию цифры. Чтобы предотвратить пу­таницу, можно писать буквы вверх ногами, если они выполняют функцию цифры.

Перевод шестнадцатеричных чисел в десятичную систему счисления

Преобразование шестнадцатеричных чисел в десятичную систему счисле­ния происходит по известному алгоритму. Целесообразно составить табли­цу согласно рис. 8.17а. Количество столбцов этой таблицы определяет наи­большее возможное шестнадцатеричное число.

Пересчет шестнадцатеричного числа А24F в десятичное производится следующим образом:

Перевод десятичных чисел в шестнадцатеричную систему счисления

При преобразовании десятичных чисел в шестнадцатеричные возникают не­большие сложности. Предлагается использовать таблицу на рис. 8.17а. Со­держимое столбцов известно, и содержимое каждого столбца может быть равно от 0 до 15. Нужно записать в таблицу цифры от 0 до Т⁷. Составим справочную таблицу, в которой содержимое всех ячеек умножено на соответ­ствующую степень числа 16. Такая таблица до 16⁴ представлена на рис. 8.18.

Если нужно представить десятичное число 1982 как шестнадцатеричное, то следует составить таблицу согласно рис. 8.19. Столбец 16³ не требуется. Теперь в таблице на рис. 8.18 ищется самое большое число, равное или мень­ше 1982.Это число 1792 = 7 • 256 = 7 • 16². В столбец 16² записывается цифра 7.

Число 1792 уже задействовано. Остается еще остаток 190:

1982

–1792

190

Теперь ищется наибольшее число из таблицы на рис. 8.18, которое рав­но или меньше 190. Это число 176 = 11 • 16¹. В столбец 16¹ заносится цифра В. Остается остаток 14:

190

–176

14

Остаток от 14 — это 14 = 14 • 16°. В столбец 16° записывается цифра Е. И остаток израсходован:

14

–14

0

Искомое шестнадцатеричное число: 7ВЕ.

В качестве следующего примера преобразуем десятичное число 50 860 в шестнадцатеричное. Самое большое число в таблице на рис. 8.18, которое равно или меньше, чем 50 860 — это, 49 152 = 12 • 4096 = 12 • 16³. Итак, в столбец 16³ заносится шестнадцатеричная цифра двенадцать, то есть С.

В столбец 16² заносится шестнадцатеричная цифра 6, так как 6 • 16² = 6 • 256, или 1536 (табл. на рис. 8.18). Остается остаток от 1708 — 1536 = 172. В стол­бец 16¹ записывается шестнадцатеричная цифра А, так как 10 • 16 = 160. Остается остаток 12. В столбец 16° заносится шестнадцатеричная цифра 12 = С. Десятичное число 50860 преобразовано в шестнадцатеричное чис­ло С 6АС.

Правильность преобразования проверяется обратным преобразованием шестнадцатеричного числа в десятичное.

Проверка: