
- •Вычитание двоичных чисел
- •Вычитание в дополнительном коде
- •Отрицательные двоичные числа
- •Сложение в bcd-формате
- •Вычитание в bcd-формате
- •Другие тетрадные системы счисления
- •Код Айкена
- •Код Грея
- •Перевод двоичных чисел в шестнадцатеричную систему счисления
- •Преобразование восьмеричных чисел
- •Дополнительный двоичный код
- •Код Хемминга
Другие тетрадные системы счисления
Из множества тетрадных систем счисления, существующих наряду с двоично-десятичным кодом, рассмотрим только три самых важных. Другие тетрадные системы играют второстепенную роль и применяются только для специальных заданий.
Код с избытком три
В коде с избытком 3 не используются первые и последние три из 16 возможных тетрад. Эти шесть тетрад являются псевдотетрадами (рис. 8.11).
Если рассматривать тетрады кода с избытком 3 в виде двоичных чисел, то видно, что их значения все время на три больше, чем значение соответствующей десятичной цифры. Десятичное число 4 представляется как 0111, то есть двоичным числом семь. Получается симметричный код (см. рис. 8.11).
Как и в двоично-десятичном коде каждая десятичная цифра представляется тетрадой.
Пример——————————————————————————————
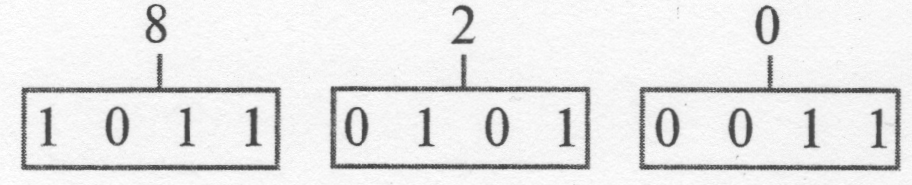
Преимуществом кода с избытком 3 является отсутствие тетрады 0000. Так как часто принимаются соотношения 0 = 0 В и 1 = U 5, то тетрада 0000 получается при исчезновении напряжения. Еще одним преимуществом является простое образование дополнения до 9.
Дополнение до 9 в коде с избытком 3 получается простым инвертированием. |
Пример——————————————————————————————
Найти дополнение до 9 к 0111 = 4(10).
0 |
1 |
1 |
1 |
|
↓ |
↓ |
↓ |
↓ |
Инверсия |
1 |
0 |
0 |
0 |
= 5(10) |
Если прибавить к дополнению до 9 единицу, то получается дополнение до десяти. Для сложения в коде с избытком 3 действуют следующие правила коррекции.
Если при сложении двух тетрад не возникает переноса в 5-й разряд, то от результата следует отнять число 0011. |
Если при сложении двух тетрад возникает перенос в 5-й разряд, то к каждой тетраде результата следует прибавить число 0011. |
Пример——————————————————————————————
|
1 |
+ 3 |
4 |
-
1
0
1
0
0
0
1
1
0
1
0
1
0
1 |
0 |
1 |
0 |
- 0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
=4
Пример——————————————————————————————
-
1
1
0
0
1
1
1
0
0
1
0
1
0
1
6 |
+ 9 |
15 |
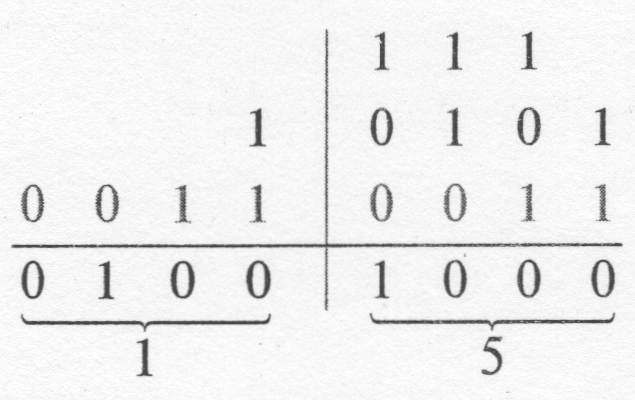
Коррекция осуществляется посредством переноса в 5-й разряд. Эта операция легко осуществима в современной цифровой технике.
