Практична частина

Дана модель розімкнутої системи, записана у вигляді відношення добутків типових ланок:

.

Необхідно:

1. Побудувати кореневий годограф.

2. Отримати коефіцієнт підсилення K^кр, при якому система знаходиться на межі стійкості.

3. Обчислити частоту ω^кр, при якій в системі виникають незгасаючі коливання.

4. Нанести на гілки кореневого годографа значення полюсів замкнутої системи, що відповідають 0,5∙K^кр і 0,25∙K^кр.

5. Привести вираз для W_З(s) у вигляді добутку типових ланок. Вказати значення параметрів типових ланок.

У ряді випадків, що мають практичне значення, модель лінійної системи автоматичного керування (САК) задається у вигляді структурної схеми, що складається з типових ланок, математичний опис яких задано в операторної формі. Зв'язок між входом і виходом системи задається у вигляді передаточної функції W(s). B загальному вигляді передаточну функцію W(s) можна представити у вигляді:

, (1)

де s – комплексна змінна, B(s) – поліном степеня m; A(s) – поліном степеня n.

Для фізично реалізованих САК m £ n. Коефіцієнти зазначених поліномів – дійсні числа.

Застосування методу кореневого годографа (КГ) обумовлено фундаментальною залежністю поведінки лінійної САК від полюсів і нулів її передаточної функції. Під полюсами маються на увазі корені полінома – знаменника A(s), а під нулями – корені полінома чисельника B(s). Поліном A(s) називається також характеристичним многочленом передаточної функції W(s).

Положення полюсів W(s) на комплексній площині визначає стійкість САК, а в сукупності з нулями вид імпульсної перехідної функції w(t) і перехідної функції h(t).

Метод кореневого годографа дозволяє знаходити полюси і нулі передаточної функції замкнутої системи, маючи полюси і нулі розімкнутої системи при зміні коефіцієнта підсилення розімкнутої системи К. Метод кореневого годографа є також методом проектування пропорційного сталого регулятора.

Передаточну функцію розімкнутої системи W_p(s) задамо у вигляді:

, (2)

де – нулі передаточної функції W_p(s), ; – полюси передаточної функції W_p(s), , n і m – порядки знаменника і чисельника; K – коефіцієнт підсилення розімкнутої системи; C – коефіцієнт представлення.

Передаточна функція розімкнутої системи, як правило, задається у вигляді відношення творів передавальних функцій стандартних (типових) ланок, при описі яких використовуються вирази трьох видів:

, (3)

, (4)

. (5)

тут Т – постійна часу [с].

Якщо вирази (3), (​4), (5) стоять у знаменнику передавальних функцій ланок (у чисельнику 1), то ланки називаються відповідно: інтегруючою, аперіодичною, коливальною. Для коливального ланки ξ – безрозмірний коефіцієнт згасання (0< ξ <1). Якщо вирази (3), (​​4), (5) стоять в чисельнику передавальних функцій ланок (1), то ланки називаються відповідно: диференціюючою, форсуючою першого порядку, форсуючою другого порядку.

Для переходу від стандартної форми запису до формули (2) необхідно обчислити полюси і нулі відповідних типових ланок.

Для передавальних функцій, що використовують вираз (3):

, (6)

для тих. що використовують вираз (4):

, (7)

для тих, що використовують вираз (5):

, (8)

або

, (9)

де .

Коефіцієнт представлення (подання) C обчислюється за формулою:

. (10)

Зауваження. Для ланок, що використовують вираз (5), відповідна постійна часу входить у вираз (10) в квадраті.

При замиканні системи з передаточною функцією W_p(s) одиничним зворотним зв'язком, передатна функція замкнутої системи W_З(s) приймає вигляд:

, (11)

де знак «+» відповідає негативному зворотному зв'язку; знак «–» відповідає позитивному зворотному зв'язку.

Структурна схема системи зі зворотним зв'язком наведена на рис. 1.

Рис. 1. Структурна схема САК

З (11) випливає, що нулі передаточної функції замкнутої системи дорівнюють нулям передаточної функції розімкнутої системи.

Задачу можна представити таким еквівалентним чином. Є об'єкт управління, який визначається передаточною функцією:

.

Необхідно знайти значення параметру пропорційного регулятора (рис. 2).

Рис. 2. Еквівалентна схема САК

Для визначення полюсів замкнутої системи (рис. 1.) Необхідно розв’язати рівняння:

W_p(s) = – 1 . (12)

Так, як W_p(s) є функцією комплексної змінної s, то рівняння (12) розпадається на два рівняння:

– Рівняння модулів:

|W(s)| = 1 (13)

– Рівняння аргументів для від’ємного зворотного зв'язку:

аrg W(s) = ± (2u +1)π, u = 0, 1, 2, ... (14а)

та для додатного зворотного зв'язку:

arg W (s) = ± 2p, u = 0, 1, 2, ... (14б)

Рівняння (14) мають наочний геометричний зміст. Якщо точка s є полюсом замкнутої системи, то, провівши в точку s вектора з усіх нулів W_p(s) (позначимо аргументи цих векторів ) і вектора з усіх полюсів W_p(s) (позначимо аргументи цих векторів ), рівняння (14а) можна записати в наступному вигляді:

, (15а)

а рівняння (14б) можна записати у вигляді:

. (15б)

Кути відраховуються від позитивного напрямку дійсної осі. Знак кута «+» відповідає повороту проти годинникової стрілки, знак кута «–» відповідає повороту за годинниковою стрілкою.

Геометричне місце точок на комплексній площині «s», яке задовольняється виразами (15а) і (15б) – називається кореневим годографом.

Як випливає з (2.15), конфігурація кореневого годографа не залежить від коефіцієнта посилення K, але кожному конкретному значенню K однозначно відповідають точки на кореневому годографа.

Для визначення цієї відповідності достатньо скористатися рівнянням (2.13) в такій інтерпретації:

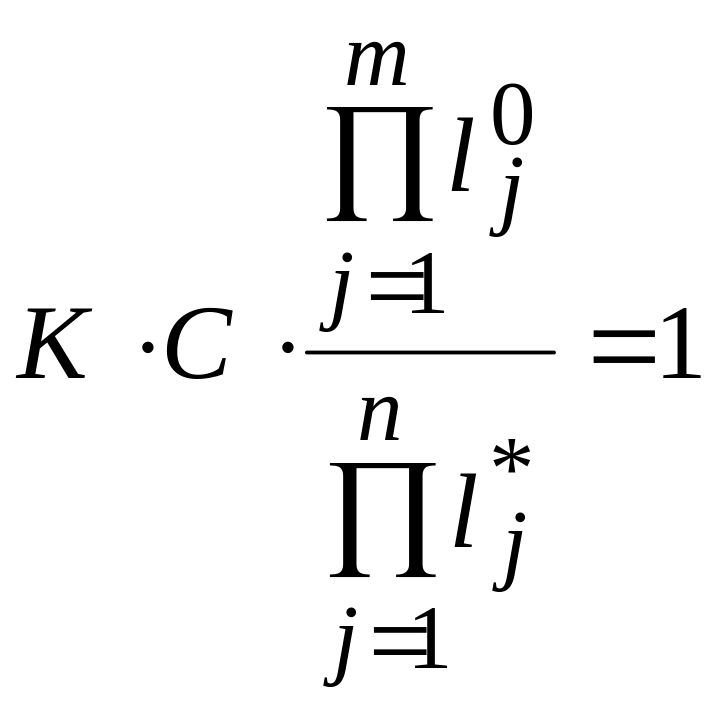(16)

де – модуль (довжина) вектора, проведеного з j-нуля в точку s КГ; – модуль вектора, проведеного з i-полюса в ту ж точку s.

Наведемо властивості кореневих годографів (випадок від’ємного зворотного зв'язку):

1. Гілки кореневого годографа неперервні і розташовані на комплексній площині симетрично щодо дійсної осі.

2. Число гілок КГ одно порядку системи n. Гілки починаються в n полюсах розімкнутої системи при K=0. При зростанні K від 0 до незкінечності, полюса замкнутої системи рухаються по гілках КГ.

3. Відрізки дійсної осі, по яких переміщаються дійсні полюси замкнутої системи – є дійсними гілками КГ. Ці гілки знаходяться в тих частинах дійсної осі, праворуч від яких розташовано непарна загальна кількість дійсних полюсів і нулів розімкнутої системи.

4. m гілок КГ при зростанні K від 0 до незкінечності закінчуються в m нулях W_p(s), a (n–m) гілок при K, прагне до нескінченності, віддаляються від полюсів вздовж асимптот.

5. Асимптоти у вигляді зірки з (n–m) напівпрямі виходять з точки з координатою:

на дійсній осі під кутами:

до дійсної осі.

6. Кут виходу гілки КГ з полюса визначається з рівняння (15а), застосованого до даного полюса. Аналогічно визначається кут входу гілки КГ в нуль .

7. При розташуванні гілок КГ в лівій півплощині s, САК стійка. При перетині гілок КГ уявної осі зліва направо САК стає нестійкою. Нехай при K = K^кр перетин КГ з уявною віссю відбудеться в деякій точці iω^кр. Назвемо це значення коефіцієнта посилення критичним K^кр, а величину ω^кр – критичною кутовою частотою, на якій система стає нестійкою.

Метод КГ дозволяє вибрати коефіцієнт підсилення САК, підібрати розташування полюсів і нулів передаточної функції коригуючих ланок, визначити параметри домінуючих полюсів САК (найближчих до початку координат площини s).