6.8 Фазовые переходы второго рода. Жидкий гелий. Сверхтекучесть

Существуютфазовые переходы второго рода, при которых некоторые свойства вещества изменяются скачком. Характерной особенностью таких переходов является отсутствие теплоты перехода. К фазовым переходам второго рода относятся такие переходы как потеря ферромагнитных свойств при переходе через точку Кюри, переход проводника в сверхпроводящее состояние, переход гелия I в гелий II. Рассмотрим фазовый переход второго рода на примере жидкого гелия. Жидкий гелий замечателен тем, что это самая холодная жидкость в природе. Наиболее важной особенностью жидкого гелия является существование двух его модификаций, переходящих одна в другую при температуре 2,186 К при атмосферном давлении. Эти модификации называют Не-I и Не-II. Точка перехода Не-I в Не-II называется λ- точкой из-за вида кривой температурной зависимости теплоёмкости жидкого гелия, напоминающей букву λ (рис.6.10).

П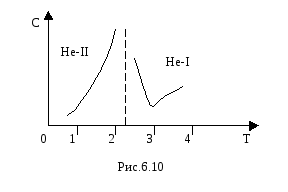ереход Не-I в Не-II происходит без выделения или поглощения скрытой теплоты, что говорит о фазовом переходе второго рода. Свойства этих модификаций гелия различны. Не-I –бесцветная жидкость, бурно кипящая с обильным выделением пузырьков.( Не-II низкотемпературная модификация) - спокойная жидкость с отчётливой поверхностью, обладающая чрезвычайно высокой теплопроводностью и сверхтекучестью. Сверхтекучесть Не-II открыл в 1938 году П.Л.Капица (нобелевский лауреат). Объяснение этого явления было дано в 1941 году Л.Д.Ландау на основе квантово-механических представлений о характере теплового движения в жидком гелии. Течение жидкого Не-II происходит так, как будто его вязкость равна нулю. Это значит, что он может свободно протекать через самые тонкие капилляры, щели, отверстия, непроницаемые даже для газов. В тонких капиллярах (диаметром 10^-4 ÷10^-5 см) течение жидкого Не-II уже не определяется уравнением Пуазейля и скорость течения его не зависит от разности давлений и длины капилляра. Однако, существует определённая критическая скорость, выше которой начинают действовать силы трения и движение становится вязким. Величина критической скорости повышается с понижением температуры и при самых низких температурах становится постоянной. На поверхности всякого твёрдого тела, соприкасающегося с жидким Не-II образуется тонкая движущаяся плёнка. Она движется в сторону, где температура выше. Если поверхность тела имеет одинаковую температуру, меньшую температуры λ- точки, и часть тела не погружена в жидкий гелий, то не погруженная часть поверхности покрывается тонкой плёнкой. В жидком Не-II наблюдается термомеханический эффект, который заключается в том, что, когда в тонком капилляре существует поток тепла, то в направлении, противоположном этому потоку, возникает поток жидкости.

Жидкий Не-II ещё и сверхтеплопроводен. Теплопроводность при переходе через λ- точку возрастает в 5 ^.10⁶ раз и становится лучше, чем у металлических проводников тепла.

6.9 Явления переноса в жидкостях

В жидкостях явления переноса подчиняются тем же уравнениям, что и в газах, но механизм процессов и коэффициенты переноса отличаются от таковых в газах. В жидкостях теряет смысл понятие «средняя длина свободного пробега молекул», поскольку силами взаимодействия между молекулами жидкости пренебречь нельзя. В жидкостях молекула, колеблющаяся около положения равновесия вследствие теплового движения, может получить от соседних молекул избыточную энергию, достаточную для скачка на некоторое расстояние δ. На новом месте частица проведёт некоторое время- время осёдлой жизни, совершая тепловые колебания, пока снова не получит достаточную для скачка энергию. Такие тепловые колебания, сменяющиеся скачками, и есть тепловые движения молекул жидкости. При определении коэффициентов переноса будем использовать средние характеристики. Коэффициент диффузии в жидкости будет выражаться формулой:

, (6.25)

где- средняя скорость молекулы, -среднее время осёдлой жизни. Коэффициент диффузии жидкостей с повышением температуры сильно возрастает из-за уменьшения среднего времени осёдлой жизни. Длительность пребывания молекулы в данном месте определяется вероятностью получения энергииW, достаточной для скачка, которая называется энергией активации молекулы. Вероятностью получить энергию W можно выразить следующим образом:

, (6.26)

где n_o – концентрация молекул с энергией порядка величины kT, n – концентрация молекул с энергией W. Время осёдлости определяется выражением , где А – период колебаний молекулы. Другие коэффициенты переноса можно выразить через введённые здесь параметры. Следует отметить, что с повышением температуры вязкость жидкостей уменьшается (в отличие от газов, у которых она возрастает), поскольку вероятность получить энергию активации, возрастает, а время осёдлости уменьшается. Коэффициент вязкости жидкостей можно выразить формулой:

(6.27)

Здесь С – множитель, зависящий от дальности скачка δ. Экспериментально коэффициент вязкости жидкостей можно измерить с помощью приборов вискозиметров. В большинстве вискозиметров (капиллярных вискозиметрах) используется формула Пуазейля:

, (6.28)

где r – радиус капилляра, ℓ - длина капилляра, V –объём жидкости, протекающей по капилляру в единицу времени под действием разности давлений ∆Р.

В некоторых вискозиметрах используется формула Стокса, тогда коэффициент вязкости рассчитывают по формуле:

(6.29)

Здесь ρ – плотность тела (например, шарика), падающего в жидкости, ρ_ж – плотность жидкости, r –радиус капилляра, - скорость падения тела.

Теплопроводность в жидкостях осуществляется благодаря тому, что более энергичные частицы совершают колебания с большей амплитудой и при столкновении с другими частицами раскачивают их, передавая им энергию. Такой механизм передачи не обеспечивает быстрого переноса энергии, поэтому теплопроводность жидкостей мала, хотя и превосходит теплоёмкость газов.