Геометрический, физический и экономический смысл производной

1. Если - некоторая функция и точка , то величина равна тангенсу угла наклона касательной к графику данной функции в точке с абсциссой (угол отсчитывается от положительного направления оси против часовой стрелки).

2. Если функция задаёт закон прямолинейного перемещения точки в зависимости от времени , то мгновенная скорость в момент времени вычисляется по формуле

.

3. Если функция задаёт зависимость затрат производства от объёма производимой продукции, то величина называется предельными затратами производства и приблизительно равна затратам на выпуск одной дополнительной единицы продукции.

4. Если функция показывает количество произведённой продукции за время , то производительность труда в момент времени равна .

Полный дифференциал функции. Производные и дифференциалы высших порядков

Определение 4.3. Производной - го порядка называется производная от производной - го порядка

.

В частности, производная второго порядка обозначается и вычисляется по формуле

при условии, что указанный предел существует. Физический смысл второй производной заключается в следующем: если закон прямолинейного движения точки задан формулой (где - время, - пройденный путь), то величина показывает скорость изменения скорости и называется ускорением точки в момент времени .

Пример 4.10. а) ;

б) .

Определение 4.4. Если функция имеет в точке конечную производную , то выражение называется дифференциалом функции в точке и обозначается

или, с учётом соотношения ,

.

Из определения и свойств производной вытекают арифметические свойства дифференциала функции

; ; .

Применение производной для нахождения пределов

Правило Лопиталя. Предел отношения двух бесконечно малых (или бесконечно больших) функций равен пределу отношения их производных (при условии, что последний существует)

.

Пример 4.11. ;

= = = = ;

= = = = = ;

= = = = ;

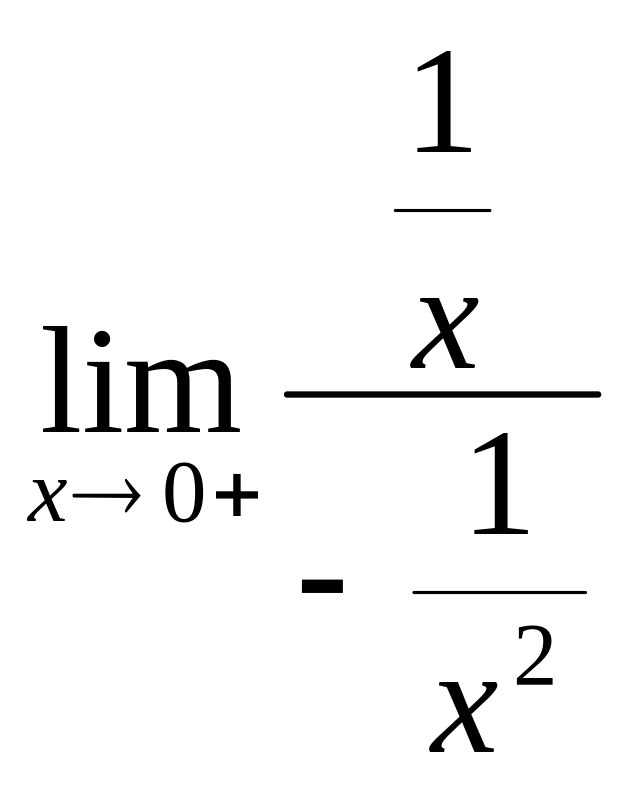- выполнить самостоятельно.

Замечание. Правило Лопиталя является эффективным, но не универсальным способом раскрытия неопределённостей. Так, например, при вычислении = = предел отношения производных не существует, поскольку не существует . Однако исходный предел существует = .

Применение производной для нахождения промежутков монотонности функции

Вспомогательные результаты

Теорема 4.5 (Лагранжа). Пусть функция непрерывна на сегменте и дифференцируема на интервале , тогда .

Следствие. Пусть функция непрерывна на сегменте и дифференцируема на интервале , тогда если выполняется соотношение , то справедливо равенство .

Основные результаты

Определение 4.5. Функция называется возрастающей (убывающей, неубывающей, невозрастающей) на промежутке , если таких, что , имеет место неравенство ( , , соответственно). Общее название таких функций – монотонные.

Теорема 4.6 (достаточное условие монотонности). Если производная функции является положительной (отрицательной) внутри некоторого промежутка , то функция возрастает (убывает) на данном промежутке.

Доказательство. Выберем так, чтобы . По теореме Лагранжа . Каждый из сомножителей в правой части положителен, следовательно, или , то есть функция является возрастающей.

В качестве примера можно привести функцию , которая является монотонно убывающей на каждом из промежутков и .

Замечание. Данное условие не является необходимым. Так, например, функция (график – кубическая парабола) возрастает на всей числовой прямой, однако .