-
Вынужденные колебания под действием гармонической силы.
-
вывод уравнения вынужденных колебаний
Все реальные колебания являются затухающими. Чтобы реальные колебания происходили достаточно долго нужно периодически пополнять энергию колебательной системы, действуя на нее внешней периодически изменяющейся силой:
(84)
где
- частота вынуждающей силы.
Запишем уравнение динамики:
(85)
(86)
(87)
(88)
|
|
- дифференциальное уравнение второго порядка вынужденных гармонических колебаний.
|
-
решение уравнения вынужденных колебаний
Решением уравнения (88) является уравнение:
(89)
При приложении внешней силы сначала возникает переходное состояние, при котором физическая система участвует одновременно в двух колебаниях, поэтому решением уравнения (88) будет выражение, состоящее из двух слагаемых:
(89)
где
- решение затухающего колебания
- решение незатухающих периодических
колебаний с вынуждающей частотой
(90)
где А – амплитуда вынужденных колебаний
- сдвиг фаз между смещением и вынуждающей
силой
Установившиеся вынужденные колебания являются так же гармоническими.
Найдем значение амплитуды А и начальной
фазы
.
Для этого запишем уравнение для скорости и ускорения и подставим их в (88)
(91)
(92)
(93)
Для упрощения решения можно воспользоваться методом векторных диаграмм:
Из рисунка видно, что
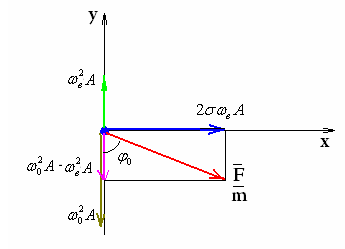
(94)
Результирующая амплитуда равна:
(95)
Из рисунка найдем начальную фазу
результирующего колебания
(
сдвиг фаз между смещением и вынуждающей
силой):
(96)
-
механический резонанс
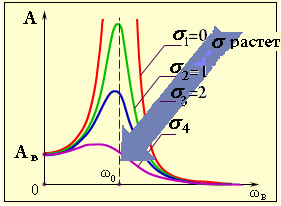
Механическим резонансом называют явление резкого возрастания амплитуды колебаний при
(97)
Т.к амплитуда вынужденных колебаний
зависит от частоты вынуждающей силы,
построим зависимость А(
)
и
.
При
подкоренное выражение в (95) будет
принимать минимальное значение, будет
иметь вид:
(98)
Если функция имеет минимум, то ее производная равна нулю, тогда
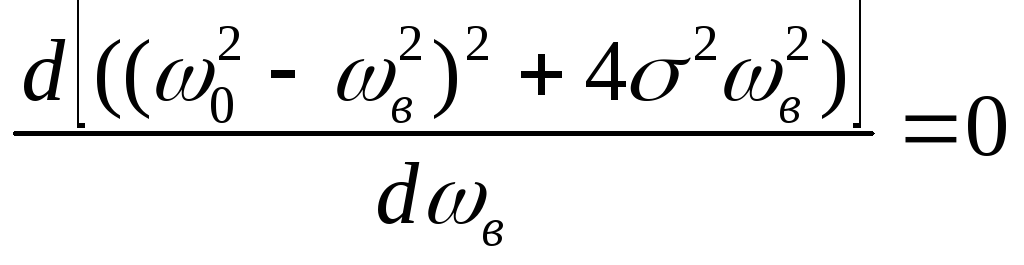(99)
(100)