2. Метод векторных диаграмм.

Ч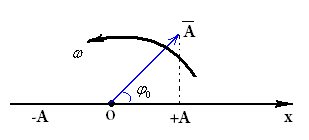асто бывает довольно удобно находить амплитуду результирующего колебания при сложении двух колебаний методом векторных диаграмм.

• проводят ось OX;

• отмечают на ней точку О и откладывают от нее вектор

Если вектор привести во вращение с частой , то проекция вектора на ось будет изменяться в пределах от –А до +А.

3. Сложение колебаний одного направления.

Пусть груз, закрепленный на потолке вагона, совершает колебания по закону:

(36)

Колебания вагона совершаются по закону:

(37)

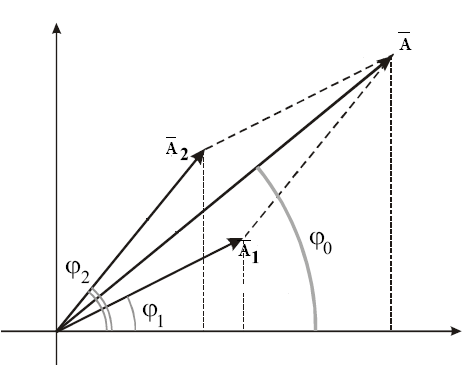
Изобразим оба колебания с помощью векторной диаграммы:

Из рисунка амплитуда результирующего колебания равна:

(36)

(37)

Начальная фаза результирующего гармонического колебания равна:

(38)

Вывод: из уравнения (37) следует, что амплитуда результирующего колебания зависит от разности фаз складываемых колебаний.

3. Представление колебаний в комплексном виде.

Для примера возьмем два уравнения для координат: и .

Согласно принципу суперпозиции эти уравнения можно представить в виде их композиции, т.е. у.

, (39)

где и - некоторые постоянные, которые могут быть комплексными.

Например: и , тогда

(40)

Используя формулу Эйлера:

, (41)

Получаем (42)

- уравнение гармонических колебаний в комплексном виде

Уравнение гармонических колебаний в комплексном виде широка используется в теории колебаний, облегчает расчеты электрических цепей.

3. Энергия колебательной системы:

• кинетическая энергия ():

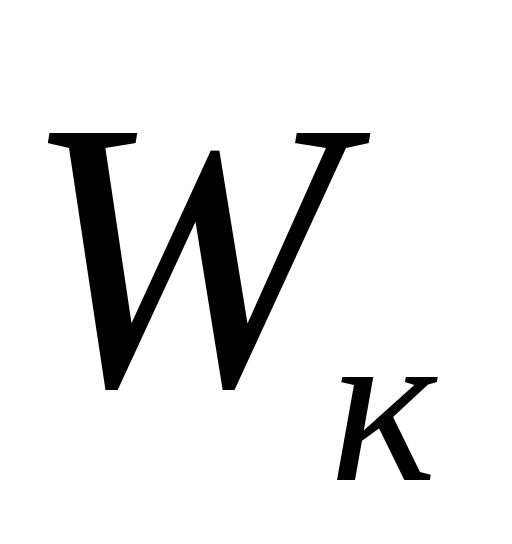В колебаниях любых систем происходит непрерывное превращение кинетической энергии в потенциальную и обратно. Например при колебаниях М.М. и Ф.М.

Кинетическая энергия системы, совершающей гармонические колебания, равна:

, (43)

где скорость изменяется по гармоническому закону:

(44)

После подстановки, имеем:

(45)

Если учесть, что (46)

и , кинетическая энергия будет равна:

(47)

Согласно формулам приведения: , получим

(48)

Вывод: физической системы совершает гармонические колебания с круговой частотой , а величина ее периодически изменяется от 0 до .

• потенциальная энергия ();

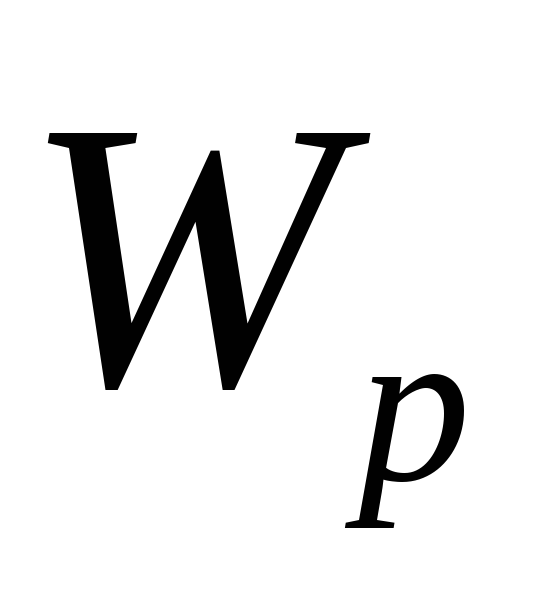Любая физическая система совершает гармонические колебания под действием квазиупругой силы, потенциальную энергию можно найти по формуле потенциальной энергии упруго-деформированного тела:

(49)

т.к. , то подставляя, получаем:

(50)

Т.к. , то , тогда

(51)

Если учесть, что (52)

и , потенциальная энергия будет равна:

(53)

(54)

Вывод: физической системы совершает гармонические колебания с круговой частотой , а величина ее периодически изменяется от 0 до .

• полная энергия гармонических колебаний ();

По определению полная механическая энергия системы равна алгебраической сумме кинетической и потенциальной энергий:

(55)

Т.к. и , то

(56)

(57)

Вывод: механической системы прямо пропорциональна и не зависит от времени.