
- •Незатухающие гармонические колебания систем с одной степенью свободы:
- •Метод векторных диаграмм.
- •Сложение колебаний одного направления.
- •Представление колебаний в комплексном виде.
- •Энергия колебательной системы:
- •Затухающие колебания с вязким трением:
- •Вынужденные колебания под действием гармонической силы.
-
Затухающие колебания с вязким трением:
-
вывод уравнения затухающих гармонических колебаний в диссипативных системах с вязким трением;
Свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системы с течением времени уменьшаются.
Кроме упругой силы, вызывающей колебания, на материальную точку действуют еще и силы сопротивления со стороны окружающей среды (силы трения).
Рассмотрим колебания шарика, подвешенного на пружинке в вертикальной плоскости в вязкой среде, которая оказывает сопротивление движению по закону Стокса:
![]() (58)
(58)
При малых колебаниях и малых скоростях
![]() .
.
![]() (59)
(59)
Результирующая сила, действующая на шарик, равна:
![]() (60)
(60)
По II закону Ньютона
![]()
![]() (61)
(61)
![]() (62)
(62)
Или
![]() (63)
(63)
Разделим все на массу:
![]() (64)
(64)
Отношение
![]() называют удвоенным коэффициентом
затухания колебаний, т.е.
называют удвоенным коэффициентом
затухания колебаний, т.е.
![]() (65)
(65)
Отношение
![]() называют квадратом циклической частоты
затухающих колебаний, т.е.
называют квадратом циклической частоты
затухающих колебаний, т.е.
![]() (66)
(66)
Тогда уравнение (64) запишется в виде:
![]() (67)
(67)
|
|
- дифференциальное уравнение второго порядка затухающих гармонических колебаний.
|
-
решение дифференциальное уравнение второго порядка затухающих гармонических колебаний
Решением дифференциального уравнения является:
![]() (68)
(68)
где
![]() - амплитуда затухания
- амплитуда затухания
![]() - некоторые постоянные
- некоторые постоянные
Из (68) следует, что зависимость x(t) будет иметь следующий вид:
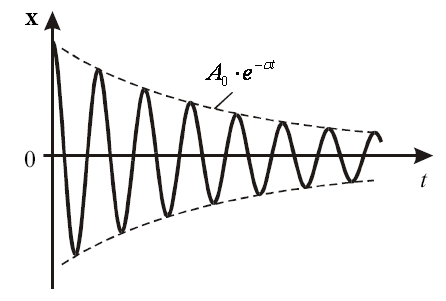
Пунктирной линией показано изменение амплитуды затухающих колебаний с течением времени.
С помощью (68) найдем скорость и ускорение:
![]() (69)
(69)
![]() (70)
(70)
![]() (71)
(71)
Подставим x,
![]() ,
,
![]() в (68):
в (68):
![]()
![]() (72)
(72)
После сокращения на
![]() и
и
![]() ,
получим:
,
получим:
![]() (73)
(73)
Одновременно Sin и Сos не могут быть равны нулю.
Выражение будет равно нулю, если каждое
из слагаемых
![]() и
и
![]() одновременно будут равны нулю:
одновременно будут равны нулю:
1.
![]()
2.
![]()
Откуда получаем:
![]() (74)
(74)
где
![]() -
коэффициент затухания,
-
коэффициент затухания,
![]() -
коэффициент сопротивления.
-
коэффициент сопротивления.
Подставим (74) в 1., получим
![]() (75)
(75)
Решая которое получаем выражение для частоты затухающих колебаний и периода:
![]() (76)
(76)
![]()
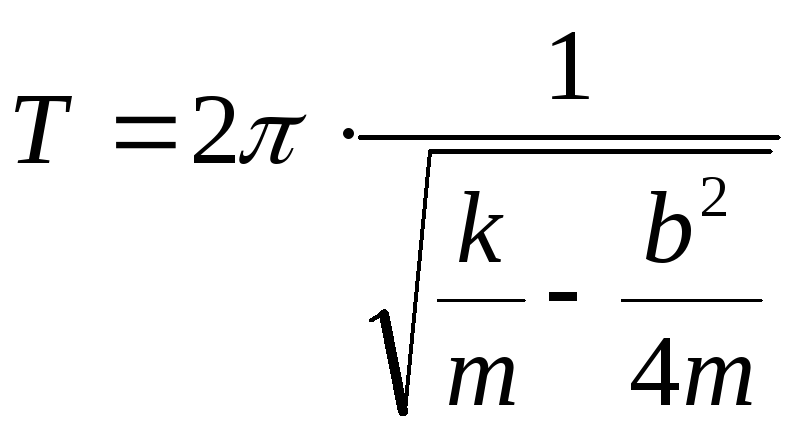 (77)
(77)
Т.к.
![]() и
и
![]() имеем выражение для частоты затухающих
колебаний:
имеем выражение для частоты затухающих
колебаний:
![]() (78)
(78)
![]() (79)
(79)
-
время релаксации
 (затухания) и коэффициент затухания
(затухания) и коэффициент затухания
Временем релаксации называют время, за которое амплитуда затухающих колебаний уменьшается в e раз.
Коэффициент затухания
![]() -
есть величина, обратно пропорциональная
времени релаксации:
-
есть величина, обратно пропорциональная
времени релаксации:
![]() или
или
![]() (80)
(80)
-
логарифмический декремент затухания

логарифмический декремент затухания прямо пропорционален произведению коэффициента затухания и периоду затухающих колебаний:
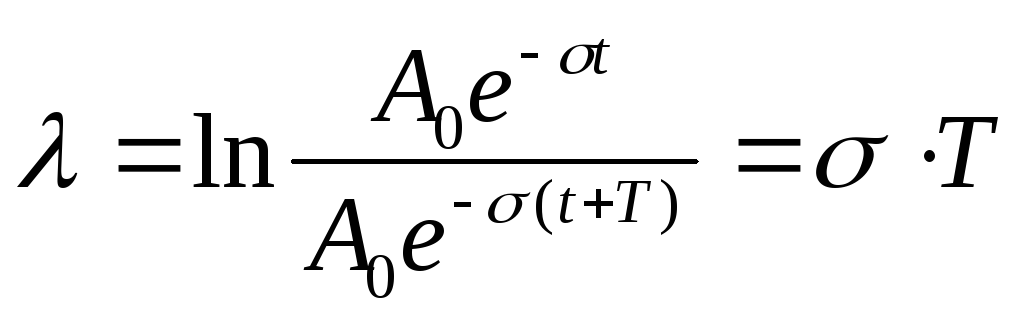 (81)
(81)
-
добротность
 (безразмерна)
(безразмерна)
Добротность – величина, характеризующая потери энергии при затухающих колебаниях.
![]() (82)
(82)
![]() или
или
![]() (83)
(83)
