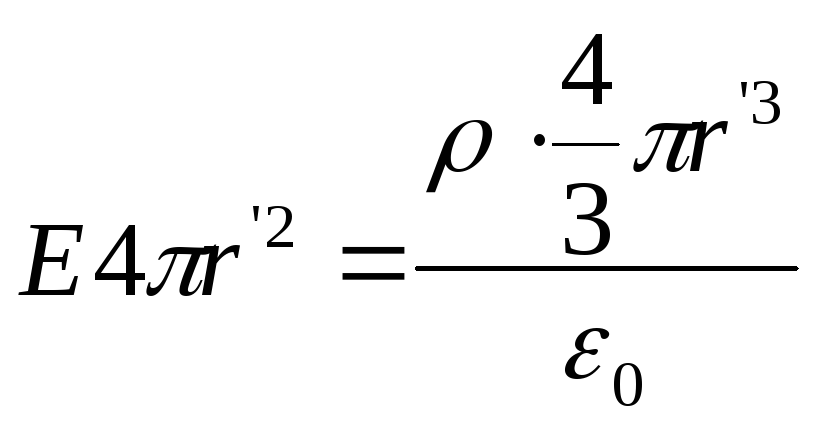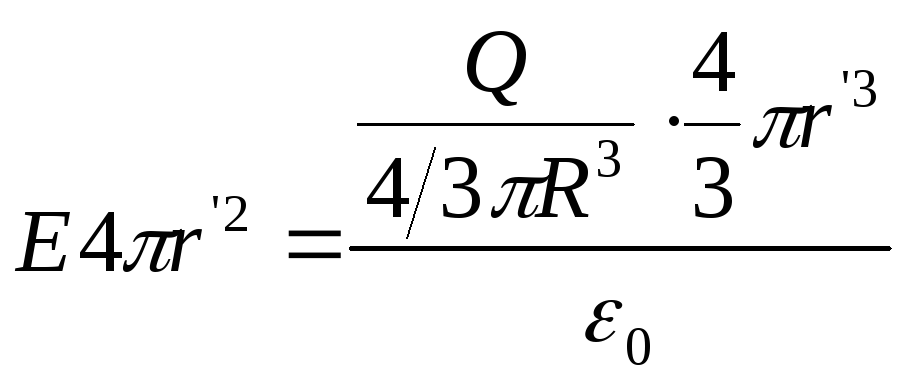- •Закон Кулона
- •Закон сохранения заряда
- •Напряженность электрического поля и электрическое смещение
- •Принцип суперпозиции электрических полей
- •Применение теоремы Гаусса к различным телам
- •Потенциал
- •Связь потенциала с напряженностью
- •Вычисление разности потенциалов по напряженности поля
- •Электроемкость. Конденсаторы
- •Энергия электрического поля
- •Поляризованность. Напряженность поля в диэлектриках
- •Примеры решения задач на закон Кулона
-
Принцип суперпозиции электрических полей
Принцип суперпозиции (наложения) электрических полей: согласно которому напряженность Е результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:
Е=E1+Е2+...+Еn (16)
В случае двух электрических полей с напряженностями Е1 и Е2 модуль вектора напряженности равен:
![]() ,
(17)
,
(17)
где — угол между векторами E1 и E2.
-
Применение теоремы Гаусса к различным телам
|
тело, рисунок
|
напряженность
|
||
|
Бесконечно заряженная плоскость
|
Рассмотрим
бесконечную плоскость, заряженную с
постоянной поверхностной
плотностью
Т.к.
поток
Тогда:
|
||
|
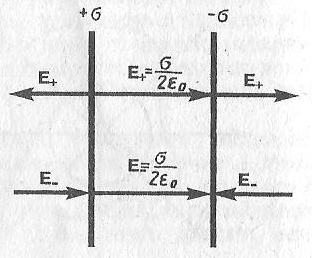
Две параллельных заряженных плоскости
|
Рассмотрим
две параллельных бесконечных плоскости,
заряженных с постоянной поверхностной
плотностью
В области между пластинами:
|
||
|
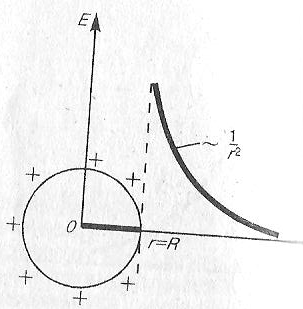
Сфера радиусом R
|
Рассмотрим
поверхность радиуса R,
заряженную равномерно с поверхностной
плотностью
а)
если r>R,
то внутрь
поверхности попадает весь заряд
При
r>R
поле
б)
если
в) на поверхности сферы (r = R)
|
||
|
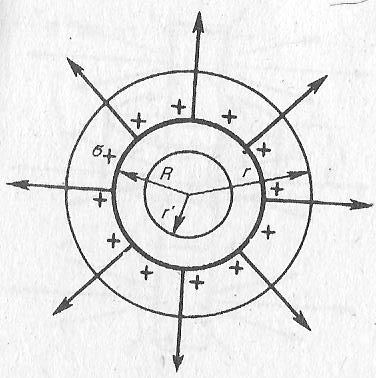
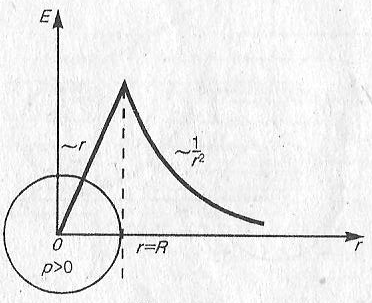
Объёмно заряженный шар
|
Рассмотрим
шар радиусом R
с общим зарядом Q,
заряженного с объемной плотностью
а)
если r>R
(см.
сферу V),
то внутрь
поверхности попадает весь заряд
б)
если
Согласно теореме Гаусса:
Т.к. объемная
плотность
|
||
|
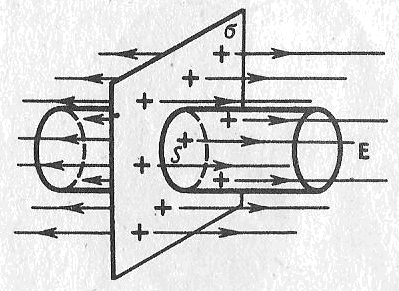
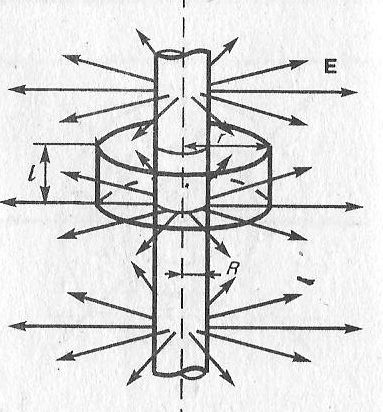
Бесконечная заряженная нить (цилиндр)
|
Рассмотрим
бесконечный цилиндр радиуса R,
который заряжен с линейной плотностью
Линии
напряженности
а)
если
б)
если
|