-
Момент импульса материальной точки,
Вектором момента импульса м.т.
относительно полюса О называют векторное
произведение радиус – вектора
и вектора импульса
относительно
этого же полюса.
Радиус-вектор
проводится от полюса О до м. т.
(9)
Направление вектора момента импульса находится по правилу правого винта и совпадает с вектором угловой скорости.
Если учесть, что
,
тогда момент импульса равен:
или
(10)
Момент количества движения твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.
Модуль вектора момента импульса равен:
,
(11)
Вектор момента импульса системы м.т. от-но полюса О равен геометрической сумме векторов моментов импульса, действующих на каждую точку в отдельности от-но того же полюса О:
(12)
или
(13)
-
Связь вектора момента силы и момента импульса
Продифференцируем (10) по времени:
(14)
Т.к. полюс неподвижен, то первое слагаемое
равно нулю (т.к. первая производная
перемещения по времени равна скорости).
Тогда
коллинеарны, а произведение коллинеарных
векторов равно нулю.
Поэтому
(15)
Согласно II закону Ньютона
,
(16)
значит (15) будет иметь вид:
или
(17)
Выражение (17) устанавливает связь между
и
.
|
связь между
|
- производная вектора момента импульса по времени относительно неподвижного полюса равна вектору момента силы, действующей на эту м.т. относительно того же полюса |
и
-
Связь момента инерции, момента силы и момента импульса и зсми
При вращении м.т. вокруг неподвижной оси выполняется условие:
Если I изменяется со временем, то получим:
или
(18)
Если
,
то
(19)
|
|
- основное уравнение динамики вращательного движения |
Закон сохранения момента количества движения: в замкнутой системе тел суммарный вектор момента импульса остается неизменным.
(20)
|
|
- закон сохранения момента количества движения |
Закон сохранения момента импульса выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера).
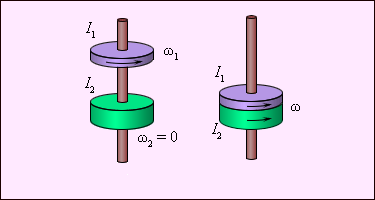
Пример, иллюстрирующий справедливость ЗСМИ связан с насаживанием дисков на ось:
