
- •Момент инерции материальной точки,
- •Момент инерции системы материальных точек
- •Теорема Штейнера
- •Момент силы,
- •Момент импульса материальной точки,
- •Связь вектора момента силы и момента импульса
- •Связь момента инерции, момента силы и момента импульса и зсми
- •Работа, совершаемая телом при вращении.
- •Мощность при вращении
- •Кинетическая энергия вращающегося тела
Филиал 3 курс 5 семестр
Лекция 3: Динамика вращательного движения
План:
-
Момент инерции материальной точки.
-
Момент инерции системы материальных точек.
-
Теорема Штейнера.
-
Таблица моментов инерции некоторых твердых тел.
-
Момент силы.
-
Момент импульса материальной точки.
-
Связь вектора момента силы и момента импульса.
-
Связь момента инерции, момента силы и момента импульса и ЗСМИ.
-
Работа, совершаемая телом при вращении.
-
Мощность при вращении.
-
Кинетическая энергия вращающегося тела.
-
Момент инерции материальной точки,
Момент инерции
м.т. (![]() )
относительно полюса – скалярная
величина, равная произведению массы
этой точки на квадрат расстояния до
полюса:
)
относительно полюса – скалярная
величина, равная произведению массы
этой точки на квадрат расстояния до
полюса:
![]() (1)
(1)
![]()
(2)
-
Момент инерции системы материальных точек
Тело можно представить состоящим из большого числа м.т., тогда момент инерции системы м.т. равен:
![]() ,
(3)
,
(3)
где
![]() - масса i
- ой м.т.
- масса i
- ой м.т.
![]() - ее расстояние до
полюса О.
- ее расстояние до
полюса О.
Моментом инерции системы м.т. или тела относительно полюса называют алгебраическую сумму произведений масс м.т., из которых состоит тело, на квадрат расстояния их до полюса О.
-
Теорема Штейнера
Для установления связи между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера:
![]() (4)
(4)
где
![]() - момент инерции относительно новой оси
- момент инерции относительно новой оси
![]() -
момент инерции относительно центра
масс
-
момент инерции относительно центра
масс
d – расстояние между осями
-
Таблица моментов инерции некоторых твердых тел
(ось проходит через геометрический центр тел)
-
тело
рисунок
момент инерции
Однородный стержень
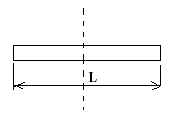

Относительно края стержня:
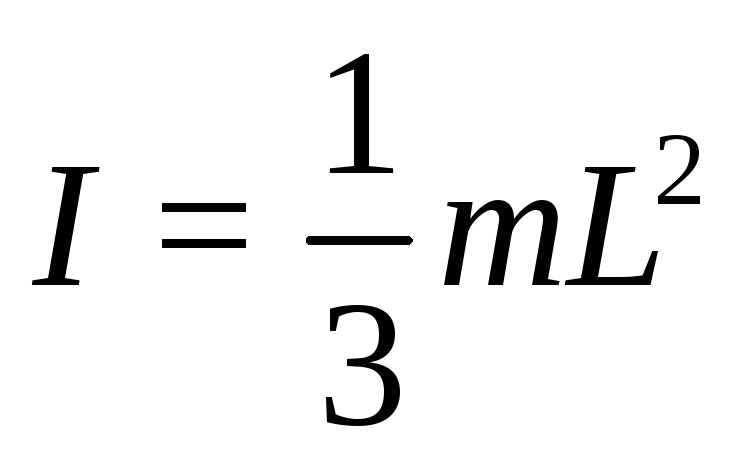
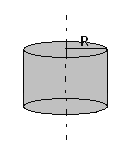
Сплошной цилиндр радиуса R.
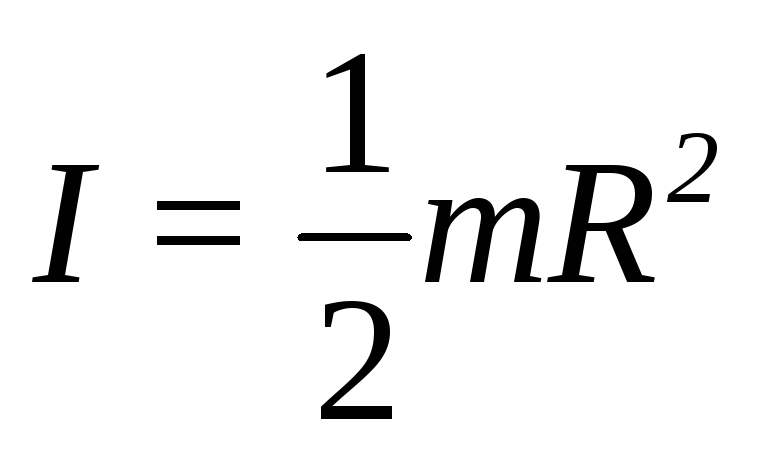
Однородный диск
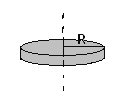
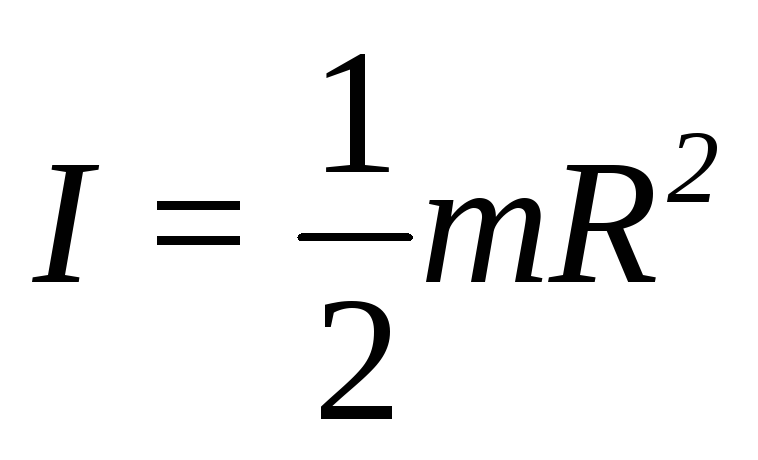
Тонкое кольцо
радиуса R.
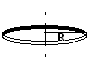
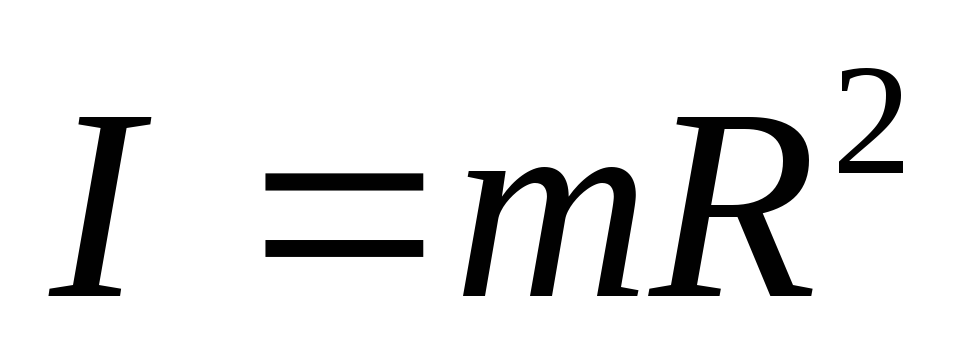
Полый цилиндр с внутренним r и внешним R радиусами
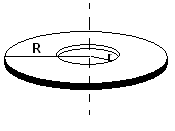
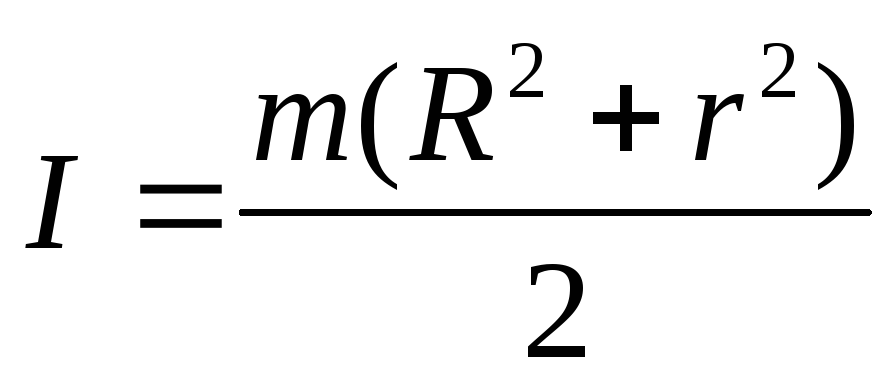
Тонкое кольцо радиусом R и ширенной d
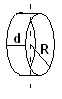
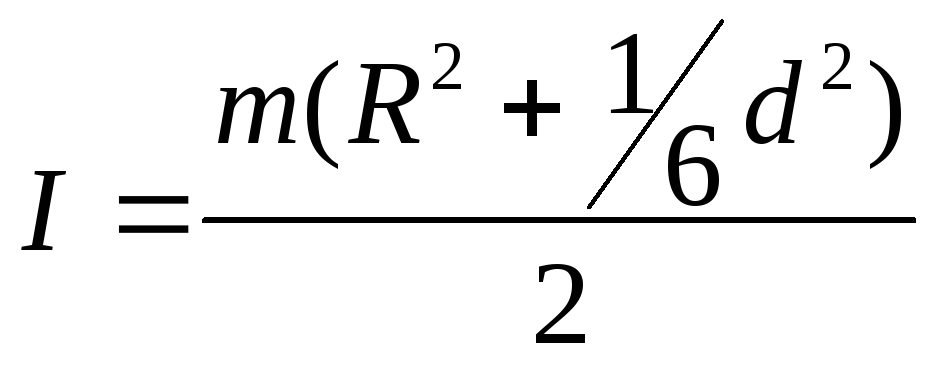
Сплошной шар
_
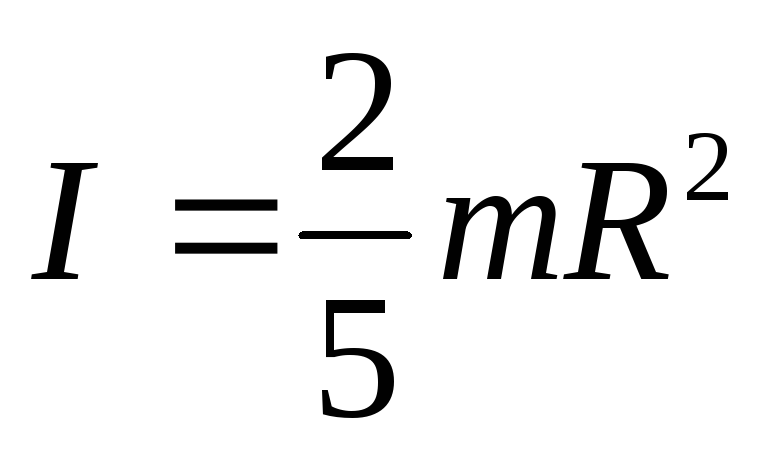
Сфера
_
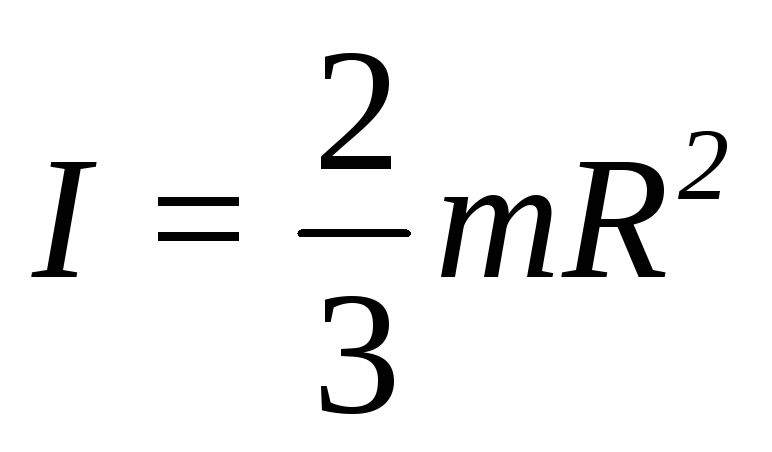
-
Момент силы,
Вектором момента силы относительно полюса называют векторное произведение радиус-вектора и вектора силы:
![]() (5)
(5)
Н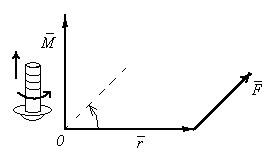 аправление
вектора момента силы находится по
правилу правого
винта (см. рис): перенесем вектор
аправление
вектора момента силы находится по
правилу правого
винта (см. рис): перенесем вектор![]() параллельно самому себе так, чтобы
совпадали начала векторов
параллельно самому себе так, чтобы
совпадали начала векторов
![]() и
и
![]() .
Если вращать головку винта в направлении
от вектора
.
Если вращать головку винта в направлении
от вектора
![]() к вектору
к вектору
![]() ,
то поступательное движение винта укажет
направление вектора момента силы
,
то поступательное движение винта укажет
направление вектора момента силы
![]() .
.
Модуль вектора момента силы равен:
![]() ,
(6)
,
(6)
где
![]() - угол между радиус-вектором и линией
действия силы.
- угол между радиус-вектором и линией
действия силы.
Момент равнодействующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил относительно того же полюса:
![]() (7)
(7)
или
![]() (8)
(8)
