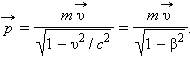10. Потенциальная энергия в поле тяготения Земли

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где — масса тела, — ускорение свободного падения, — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости. Свойством консервативности обладают наряду с силой тяжести и силой упругости некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя

Будем исследовать одномерное движение тела, при этом его потенциальная энергия является функцией лишь одной переменной (чаще всего функции координаты х), т. е. P=P(х). График зависимости потенциальной энергии от данного аргумента называется потенциальной кривой. Исследование потенциальных кривых дает возможность определить характер движения тела. В этом разделе мы рассматриваем только консервативные системы - системы, в которых отсутствуют взаимные превращения механической энергии в другие виды. Тогда справедлив закон сохранения энергии. Будем рассматривать графическое представление потенциальной энергии тела, находящегося в однородном поле тяжести и для тела, подвергающегося упругим деформациям. Потенциальная энергия тела массой m, находящегося на высоте h над поверхностью Земли: P(h)=mgh. Потенциальная кривая в этом случае: P=P(h) - прямая линия, проходящая через начало координат (рис. 1), тангес угла наклона которой к оси h: tgα=mg. Значит, чем больше масса тела, тем больше α.

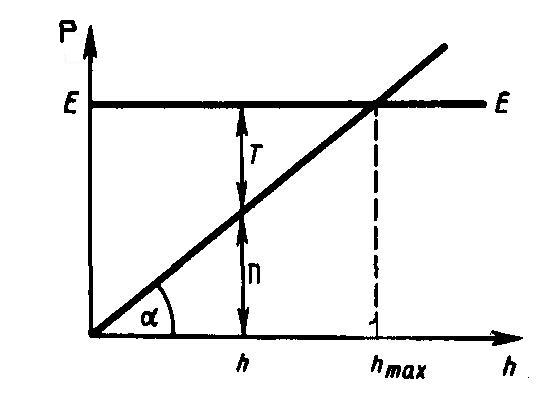
Пусть полная энергия рассматриваемого тела равна Е (на графике - прямая, параллельная оси h). Тело на высоте h обладает потенциальной энергией P, определяемая отрезком вертикали, находящимся между точкой h на оси абсцисс и графиком P(h). Очевидно, что кинетическая энергия Т задается ординатой между графиком P(h) и прямой ЕЕ, параллельной оси абсцисс. Из рис. 1 следует, что если h=h_max, то Т=0 и P=E=mgh_max, т. е. потенциальная энергия в этом случае становится максимальной и равной полной энергии. Из данного графика можно найти скорость тела на высоте h: т.е. 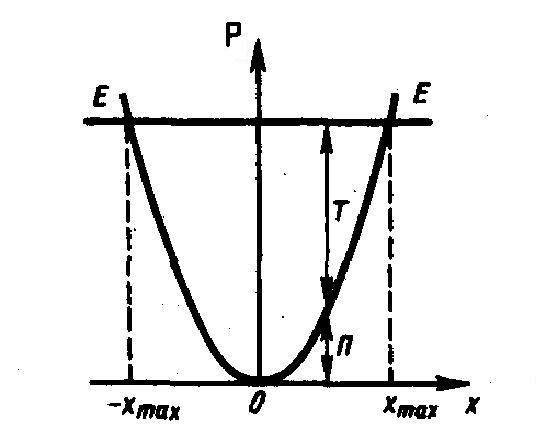откуда Зависимость потенциальной энергии упругодеформированного тела P=кх²/2 от деформации х имеет вид параболы (квадратичная зависимость) (рис. 2), где график заданной полной энергии тела Е - горизонтальная прямая (параллельная оси абсцисс х), а значения Т и P определяются так же, как на рис. 1. Из рис. 2 мы видим, что с ростом деформации х потенциальная энергия тела растет, а кинетическая - уменьшается. Абсцисса x_max показывает максимально возможную деформацию растяжения тела, a -х_max - максимально возможную деформацию сжатия тела. Если х = ±х_max, то T=0 и P=E=kx²/2, в этом случае потенциальная энергия максимальна и равной полной энергии.

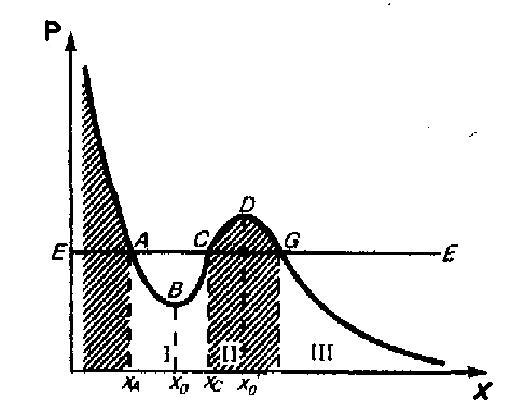
Из графика на рис. 2 вытекает, что если полная энергии тела равна Е, то тело не может сместиться правее х_max и левее -х_max, причем т.к. кинетическая энергия не может быть меньшей нуля и, следовательно, потенциальная энергия никогда не может быть больше полной энергии. В этом случае говорят, что тело находится в потенциальной яме с координатами -х_max≤x≤x_max. В общем случае потенциальная кривая может иметь сложный вид, например с чередующимися максимумами и минимумами (рис. 3). Проанализируем данную потенциальную кривую. Если Е - заданная полная энергия частицы, то частица может быть в области, где P(х)≤Е, т. е. в областях I и III. Переходить из области I в III и обратно частица не может, так как ей мешает потенциальный барьер CDG, размер которого равен интервалу значений х, при которых E < P, а его высота равна разности P_mах-E. Чтобы частица смогла преодолеть потенциальный барьер, нужно передать частице дополнительную энергию, большую или равную высоте барьера. В области I частица с полной механической энергией Е оказывается внутри потенциальной ямы AВС, при этом она совершает колебания между точками с координатами х_A и х_C. При этом в точке В с координатой х₀ (рис. 3) потенциальная энергия нашей частицы минимальна. Т.к. действующая на частицу сила (P - зависит только от одной координаты), а условие минимума потенциальной энергии , то в точке В -Fx = 0. При смещении частицы из положения х₀ (и влево и вправо) она испытывает действие возвращающей силы, поэтому положение х₀ есть положение устойчивого равновесия. Данные условия выполняются и для точки (для P_max), но эта точка соответствует положению неустойчивого равновесия, т.к. при малом смещении частицы из положения равновесия появляется сила, стремящаяся сильно сдвинуть ее от этого положения.

11.

Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона. Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и По третьему закону Ньютона Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: Применим к этим телам второй закон Ньютона:

где и – импульсы тел в начальный момент времени, и – импульсы тел в конце взаимодействия. Из этих соотношений следует:

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, то есть векторную сумму импульсов всех тел, входящих в эту систему. Рис. 1.17.1 иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде: ΣL(вектор)=const ,если система находится в равновесии.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

A = –(Ep2 – Ep1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19):

A = Ek2 – Ek1.

Следовательно

Ek2 – Ek1 = –(Ep2 – Ep1) или

Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

– сила натяжения нити в нижней точке траектории.

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:

Обратим внимание на то, что сила натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы. При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:

Из этих соотношений следует:

Центростремительное ускорение в нижней точке создается силами и направленными в противоположные стороны:

Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно

F = 6mg.

Прочность нити должна, очевидно, превышать это значение. Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач. В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды. Сила трения не является консервативной. Работа силы трения зависит от длины пути. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии. Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.

12.

Класс-ая мех-ка основана Галилео Галилеем и Иссаком Ньютоном.

Кл-кая м-ка изучает формы движ-я , сост-е в измен-и положения тел или частей тел в пространстве.

Пространство:

-бесконенчо

-абсолютно

-изотронно

-непрерывно

-трёхмерно;

Время:

-абсолютно

-непрерывно

-одномерно;

Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

Вид преобразований при коллинеарных осях^[4]

Если ИСО S движется относительно ИСО S' с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

• Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

• Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей 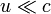(много меньше скорости света).

Преобразование скорости:

Если то средние скорости совпадают с мгновенными:

или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

13.

Постулаты Энштейна:

1 постулат Эйнштейна или принцип относительности: все законы природы инвариантны по отношению ко всем инерциальным системам отсчета. Все физические, химические, биологические явления протекают во всех инерциальных системах отсчета одинаково.

2 постулат или принцип постоянства скорости света: скорость света в вакууме постоянна и одинакова по отношении» к любым инерциальным системам отсчета. Она не зависит ни от скорости источника света, ни от скорости его приемника. Ни один материальный объект не может двигаться со скоростью, превышающей скорость света в вакууме. Более того, пи одна частица вещества, т.е. частица с массой покоя, отличной от нуля, не может достичь скорости света в вакууме, с такой скоростью могут двигаться лишь полевые частицы, т.е. частицы с массой покоя, равной нулю.

Относительность одновременности событий является ключевым эффектом СТО, проявляющимся, в частности, в «парадоксе близнецов». Рассмотрим несколько синхронизированных часов, расположенных вдоль оси в каждой из систем отсчёта. В преобразованиях Лоренца предполагается, что в момент времени начала систем отсчёта совпадают: . Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения системы отсчёта (левый рисунок) и с точки зрения наблюдателей в (правый рисунок):

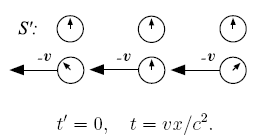
Предположим, что рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. Положив в преобразованиях Лоренца , получаем . Это означает, что наблюдатели в системе , одновременно с совпадением времени на центральных часах, регистрируют различные показания на часах в системе . Для наблюдателей, расположенных справа от точки , с координатами , в момент времени часы неподвижной системы отсчёта показывают «будущее» время: . Наблюдатели , находящиеся слева от , наоборот, фиксируют «прошлое» время часов : . На рисунках выше положение стрелок символизирует подобную разницу показаний часов двух систем отсчёта.

Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако, этого нельзя сделать одновременно для двух различных систем отсчёта.

релятиви́стским замедле́нием вре́мени обычно подразумевают кинематический эффект специальной теории относительности, заключающийся в том, что в движущемся теле все физические процессы проходят медленнее, чем следовало бы для неподвижного тела по отсчётам времени неподвижной (лабораторной) системы отсчёта.

Релятивистское замедление времени проявляется^[1], например, при наблюдении короткоживущих элементарных частиц, образующихся в верхних слоях атмосферы под действием космических лучей и успевающих благодаря ему достичь поверхности Земли.

Данный эффект, наряду с гравитационным замедлением времени учитывается в спутниковых системах навигации, например, в GPS ход времени часов спутников скорректирован на разницу с поверхностью Земли^[2], составляющую суммарно 38 микросекунд в день^[3].

В качестве иллюстрации релятивистского замедления времени часто приводится парадокс близнецов.

Количественное описание замедления времени может быть получено из преобразований Лоренца:

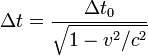
где — время, проходящее между двумя событиями движущегося объекта с точки зрения неподвижного наблюдателя, — время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя, связанного с движущимся объектом, — относительная скорость движения объекта, — скорость света в вакууме. Точность формулы неоднократно проверена на элементарных частицах и атомах^[4], так что относительная ошибка составляет менее 0,1 ppm^[4].

Аналогичное обоснование имеет эффект лоренцева сокращения длины.

14.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями.

Система отсчёта представляет собой некоторое материальное тело, выбираемое в качестве начала этой системы, способ определения положения объектов относительно начала системы отсчёта и способ измерения времени. Обычно различают системы отсчёта и системы координат. Добавление процедуры измерения времени к системе координат «превращает» её в систему отсчёта.

Инерциальная система отсчёта (ИСО) — это такая система, относительно которой объект, не подверженный внешним воздействиям, движется равномерно и прямолинейно. Постулируется, что любая система отсчёта, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, также является ИСО.

Событием называется любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x, y, z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т.п.

Обычно рассматриваются две инерциальные системы S и S'. Время и координаты некоторого события, измеренные относительно системы S, обозначаются как (t, x, y, z), а координаты и время этого же события, измеренные относительно системы S', как (t', x', y', z'). Удобно считать, что координатные оси систем параллельны друг другу, и система S' движется вдоль оси x системы S со скоростью v. Одной из задач СТО является поиск соотношений, связывающих (t', x', y', z') и (t, x, y, z), которые называются преобразованиями Лоренца.

Лоренцево сокращение, Фицджеральдово сокращение, также называемое релятивистским сокращение длины движущегося тела или масштаба — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета.

Эффект значим, только если скорость предмета по отношению к наблюдателю сравнима со скоростью света.

, где c — скорость света

15.

основу такого пересмотра Эйнштейн положил требования выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Для того, чтобы закон сохранения импульса выполнялся во всех инерциальных системах отсчета, оказалось необходимым изменить определение импульса тела. Вместо классического импульса в СТО релятивистский импульс тела с массой m, движущегося со скоростью записывается в виде

(*)

Если принять такое определение, то закон сохранения суммарного импульса взаимодействующих частиц (например, при соударениях) будет выполняться во всех инерциальных системах, связанных преобразованиями Лоренца. При β → 0 релятивистский импульс переходит в классический. Масса m, входящая в выражение для импульса, есть фундаментальная характеристика частицы, не зависящая от выбора инерциальной системы отсчета, а, следовательно, и от скорости ее движения. (Во многих учебниках прошлых лет ее было принято обозначать буквой m₀ и называть массой покоя. Кроме того, вводилась так называемая релятивистская масса, равная зависящая от скорости движения тела. Современная физика постепенно отказывается от этой терминологии).

E2 = (mc2)2 + (pc)2.

Отсюда еще раз следует, что для покоящихся частиц (p = 0) E = E₀ = mc².

Полученное соотношение показывает, что частица может иметь энергию и импульс, но не иметь массы (m = 0). Такие частицы называются безмассовыми. Для безмассовых частиц связь между энергией и импульсом выражается простым соотношением

E = pc.

К безмассовым частицам относятся фотоны – кванты электромагнитного излучения и, возможно, нейтрино. Безмассовые частицы не могут существовать в состоянии покоя, во всех инерциальных системах отсчета они движутся с предельной скоростью c.

16.

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химического вещества. В основе молекулярно-кинетической теории лежат три основных положения:

1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными и состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.

3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало

Итак, находящиеся под давлением газ или жидкость действуют с некоторой силой на любую поверхность, ограничивающую их объем. В этом случае сила действует по нормали к ограничивающей объем поверхности. Давление на поверхность равно:

,

где ΔF – сила, действующая на поверхность площадью ΔS.

Поскольку оба поршня являются стенками одного и того же сосуда, то в соответствии с законом Паскаля они испытывают одинаковое давление. Пусть – давление на малый поршень, а – давление на большой поршень. Тогда, т.к. P₁ = P₂, имеем:

,

Отсюда F₁=F₂(S₁/S₂)=0,01F₂

,

(1.2.1)

Таким образом, мы определили давление как силу, действующую в единицу времени на единицу площади:

,

(1.2.2)

под скоростью v_x²понимаем среднеквадратичную скорость <v_x²> .

,

Тогда можно записать в общем случае:

или

(1.2.3)

где <E_k>– средняя энергия одной молекулы. Это и есть основное уравнение молекулярно-кинетической теории газов.

18.

Соотношение

p = nkT,

связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:

R = 8,31 Дж/моль·К.

Соотношение

(*)

называется уравнением состояния идеального газа. Для одного моля любого газа это соотношение принимает вид:

pV=RT.

Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный

V0 = 0,0224 м3/моль = 22,4 дм3/моль.

Это утверждение называется законом Авогадро. Для смеси невзаимодействующих газов уравнение состояния принимает вид

pV = (ν1 + ν2 + ν3 + ...)RT,

где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси. Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (*) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева. Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально.

17.

Статистическая физика — раздел физики, изучающий методами теории вероятностей поведение систем частиц в состоянии равновесия или в неравновесном состоянии. Статистическую физику подразделяют на равновесную и неравновесную. Обычно при исследовании таких систем нас не интересует почти случайное поведение каждой конкретной частицы. Статистическая физика описывает, как из движений частиц системы складывается усреднённая эволюция системы в целом. Статистическая физика даёт вывод термодинамики многих реальных систем: идеальных газов, реальных газов, квантовых газов, простых конденсированных сред (например, идеальных кристаллов, спиновых цепочек). В частности, она даёт явные соотношения для используемых в термодинамике энтропии, термодинамической работы, внутренней энергии и объясняет закон неубывания энтропии. Неравновесная статистическая механика и физическая кинетика изучает, как именно система приходит в состояние локального равновесия. Методы статистической физики могут применяться не только к атомам и молекулам, но и ко многим иным системам. Соответствующий подраздел статистической физики можно назвать физикой сложных систем.

Фазовое пространство в математике и физике представляет множество всех состояний системы в фиксированный момент времени. Каждому возможному состоянию системы соответствует точка фазового пространства. Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки. Кроме того, в механике движение этой точки определяется сравнительно простыми уравнениями Гамильтона, анализ которых позволяет делать заключения о поведении сложных механических систем.

Функция статистического распределения (функция распределения в статистической физике) — одно из основополагающих понятий статистической физики. Знание функции распределения полностью определяет вероятностные свойства рассматриваемой системы.

Механическое состояние любой системы однозначно определяется координатами qi и импульсами pi ее частиц (i=1,2,…, d; d — число степеней свободы системы). Набор величин и образуют фазовое пространство. Вероятность нахождения системы в элементе фазового пространства (с точкой q, p внутри) дается формулой:

Функцию называют полной функцией статистического распределения (или просто функцией распределения).

Флуктуации — случайные отклонения от среднего значения физических величин, характеризующих систему из большого числа частиц; вызываются тепловым движением частиц или квантовомеханическими эффектами. Примером термодинамических флуктуаций являются флуктуации плотности вещества в окрестностях критических точек, приводящих, в частности, к сильному рассеянию света веществом и потери прозрачности.

Распределение Максвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла может быть получено при помощи статистической механики. Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

где является числом молекул имеющих энергию при температуре системы , является общим числом молекул в системе и , — постоянная Больцмана.

Учитывая, что плотность распределения по скоростям пропорциональна плотности распределения по импульсам:

и используя мы получим:

,

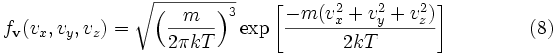что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе около скорости равна

Средняя скорость

Подставляя и интегрируя, мы получим

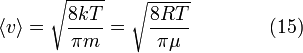
Статистика Максвелла — Больцмана — статистический метод описания физических систем, содержащих большое число невзаимодействующих частиц, движущихся по законам классической механики (то есть классического идеального газа); предложена в 1871 г. австрийским физиком Л. Больцманом.

Рассмотрим систему частиц, находящуюся в однородном поле. В таком поле каждая молекула идеального газа обладает полной энергией

, где

— кинетическая энергия её поступательного движения, а — потенциальная энергия во внешнем поле, которая зависит от её положения.

Подставим это выражение для энергии в распределение Гиббса для молекулы идеального газа (где — вероятность того, что частица находится в состоянии со значениями координат и импульсов , в интервале )

имеем:

,

где интеграл состояний равен:

интегрирование ведется по всем возможным значениям переменных. Далее интеграл состояний можно написать в виде:

мы находим, что нормированное на единицу распределение Гиббса для молекулы газа при наличии внешнего поля имеет вид:

.

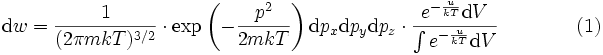Полученное распределение вероятностей, характеризующее вероятность того, что молекула имеет данный импульс и находится в данном элементе объема, носит название распределение Максвелла — Больцмана.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

где p — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

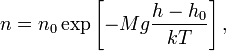
где M — молярная масса газа, k — постоянная Больцмана.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нем обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.