
- •Начальные сведения об элементарных частицах
- •1. Классификация элементарных частиц
- •1.1 Взаимодействия
- •1.2 Классификация элементарных частиц
- •Следующий класс лептоны. Это самые легкие из частиц с ненулевой инвариантной массой. Часто, в расчетах полагают, что инвариантная масса нейтрино равна нулю. Все
- •1.3 Законы сохранения во взаимодействиях
- •1.4 Упражнения для самостоятельной работы
- •Вопрос 1. Какой из атомов больше: водорода или гелия? Дайте обоснование своему ответу.
- •1.2 Неопределенность энергии и время жизни
- •2. Обменное взаимодействие
- •2.1 Виртуальное облако пиона
- •Вопрос 3. Какие экспериментальные факты указывают на то, что энергия виртуального пиона близка к нулю? Чему она равна?
- •2.2 Обменный механизм притяжения
- •Вопрос 4. В чем состоит неточность утверждения: “Ядро атома гелия состоит из двух протонов и двух нейтронов”?
- •Вопрос 5. Какие обстоятельства, кроме слабости взаимодействия с ядрами, не позволяют считать, что мюон является переносчиком адронного взаимодействия?
- •3. Домашнее задание
- •3.1 Решение задач
- •1. Скорость взаимодействия
Вопрос 5. Какие обстоятельства, кроме слабости взаимодействия с ядрами, не позволяют считать, что мюон является переносчиком адронного взаимодействия?
Задача 5. Адронное взаимодействие между нуклонами является суммой вкладов обменных взаимодействий, обусловленных не только обменом пионами, но и каонами и эта-мезонами. Почему при расчетах обычно учитывают только пионный вклад?
3. Домашнее задание
3.1 Решение задач
Задача 1. Ковалентная связь молекулы водорода описывается обменной моделью. В отличие от адронного взаимодействия переносчиком ковалентной связи является не виртуальная частица, а реальный электрон, перепрыгивающий от одного атома водорода к другому. Полагая, что в изолированном атоме водорода электрон локализован в области размером 0,5110-10 м, оцените энергию ковалентной связи молекулы водорода (работу, которую надо совершить, чтобы разорвать молекулу на атомы). Считайте, что при соединении атомов водорода в молекулу размер области локализации электрона увеличивается вдвое.
Задача 2. Среднее время жизни мюона равно 2,210-6 с. С какой точностью (в процентах) можно определить массу мюона?
взаимодействия
1. Скорость взаимодействия
1.1 Скорость распадов
При
изучении радиоактивного распада ядер
было выяснено, что число нераспавшихся
ядер к моменту времени t
описывается законом
 (1)
где
N0
число нераспавшихся ядер в момент t=0,
T
период полураспада, =T/ln2
среднее
время жизни ядра.
(1)
где
N0
число нераспавшихся ядер в момент t=0,
T
период полураспада, =T/ln2
среднее
время жизни ядра.
З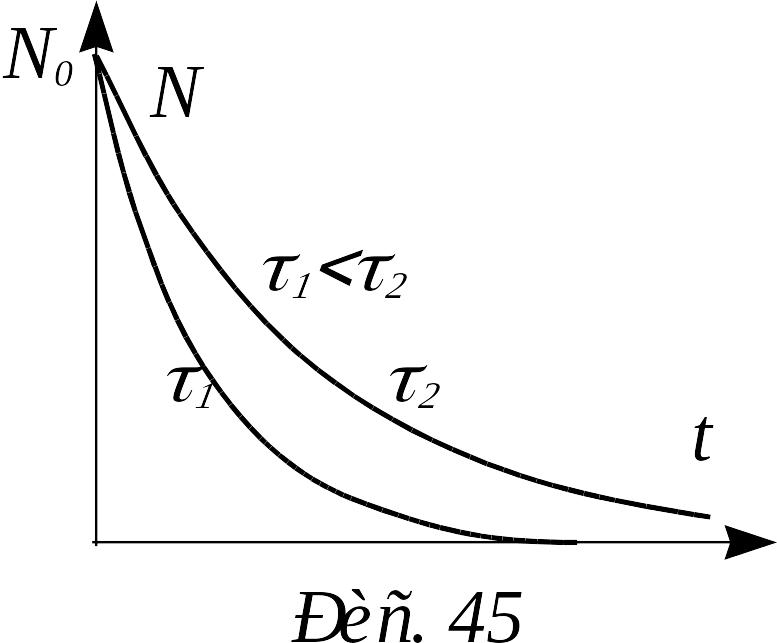 акон
изменения числа нераспавшихся частиц
N(t)
обладает рядом свойств:
график имеет вид монотонно спадающей
с течением времени функции; за равные
промежутки времени число нераспавшихся
частиц убывает в одно и то же число раз;
график идет тем круче, чем меньше
среднее время жизни. Еще одно свойство
заслуживает особого внимания. Из формулы
(1) следует, что
акон
изменения числа нераспавшихся частиц
N(t)
обладает рядом свойств:
график имеет вид монотонно спадающей
с течением времени функции; за равные
промежутки времени число нераспавшихся
частиц убывает в одно и то же число раз;
график идет тем круче, чем меньше
среднее время жизни. Еще одно свойство
заслуживает особого внимания. Из формулы
(1) следует, что
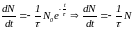 (2)
скорость
изменения числа нераспавшихся ядер в
момент времени t
пропорциональна
самому числу ядер.
(2)
скорость
изменения числа нераспавшихся ядер в
момент времени t
пропорциональна
самому числу ядер.
Опыт показал, что закон распада радиоактивных ядер является универсальным. По этому же закону убывает число нестабильных элементарных частиц одного и того же сорта. Удивительно, но закон работает и при чрезвычайно малых временах жизни частиц.
При
больших числах частиц величина N(t)/N0
равна вероятности P
уцелеть одной частице к моменту времени
t.
Например, если в момент времени t=0
число
частиц равно 100000,
а к концу первой микросекунды осталось
30000,
то значение вероятности
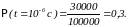 Вероятность частице в начальный момент
времени уцелеть равна 1.
Закон (1) для вероятности выглядит
так
Вероятность частице в начальный момент
времени уцелеть равна 1.
Закон (1) для вероятности выглядит
так
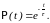 (3)
Это
общепринятая форма записи закона
распада. Из (3) следует P(0)=1.
Уравнение, связывающее скорость изменения
вероятности и саму вероятность уцелеть
согласно (2) имеет вид:
(3)
Это
общепринятая форма записи закона
распада. Из (3) следует P(0)=1.
Уравнение, связывающее скорость изменения
вероятности и саму вероятность уцелеть
согласно (2) имеет вид:
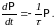 (4)
(4)
Для прояснения понятия скорости взаимодействия восстановим логику вывода закона распада (3). Определим вероятность не распасться к моменту времени t. Разобьем интервал (0, t) на N равных малых промежутков времени длительности t=t/N. Предположим, что вероятность распада P в любой промежуток времени одна и та же при условии, что к началу промежутка частица еще не распалась. Очевидно, что эта вероятность должна быть пропорциональна величине промежутка, т.е. P =t, (5) где характеристика темпа распада. Из уравнения (5) можно сделать вывод, что смысл параметра это вероятность распада в малый промежуток времени, отнесенная к этому промежутку, т.е. скорость распада. Размерность параметра []=с-1, то есть та же, что и частоты. За время t вероятность нераспада уменьшается до P1=1t. Для любого малого промежутка времени справедливо аналогичное соотношение: вероятность не распасться равна Pk=1t.
Вернемся
к рассмотрению распада частицы. Каждый
малый интервал времени t
из
всей последовательности, составляющей
интервал (0,
t),
связан со случайным событием. Для каждого
малого интервала возможно два исхода:
в этом интервале распад происходит с
вероятностью P
t
(аналог черной грани кости);
P
в этом интервале распад не происходит
с вероятностью 1–
P
t
(аналог
белых граней кости). Событие, заключающееся
в том, что к моменту времени t
частица не распадется, состоит в том,
что распад не произойдет ни в один из
малых промежутков времени. Оно представляет
совместное осуществление N
независимых событий – не распад в каждом
из N
малых
интервалов. Вероятность этого события
равна произведению N
вероятностей:
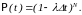 (6)
Заметим,
что t=t/n,
поэтому уравнение (6) принимает
вид:
(6)
Заметим,
что t=t/n,
поэтому уравнение (6) принимает
вид:
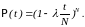 (7)
Если
сделать замену переменных (n/t)=m,
то
(7)
Если
сделать замену переменных (n/t)=m,
то
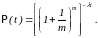 (8)
Нас,
конечно, интересует значение правой
части уравнения (8) при m
(8)
Нас,
конечно, интересует значение правой
части уравнения (8) при m .
Как ранее было установлено,
.
Как ранее было установлено,
![]() (здесь
e
основание натурального логарифма),
поэтому уравнение (8) приобретает
вид
(здесь
e
основание натурального логарифма),
поэтому уравнение (8) приобретает
вид
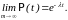 (9)
Сравнивая
(9) с выражением (3), можно сделать вывод,
что скорость распада
связана
со средним временем жизни
соотношением
(9)
Сравнивая
(9) с выражением (3), можно сделать вывод,
что скорость распада
связана
со средним временем жизни
соотношением
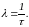 (10)
Это
же следует из уравнения (4):
(10)
Это
же следует из уравнения (4):
 (11)
(11)
Уравнения (10) и (11) можно проиллюстрировать графически. Производная от P(t) в точке t=0 равна тангенсу угла наклона касательной к графику P(t). Уравнение касательной имеет вид P=1t. (12) Касательная пересекает ось времени в точке t=1/=. Так что среднее время жизни равно времени, в течение которого при постоянной скорости распада вероятность нераспада обращалась бы в нуль. Скорость (или среднее время жизни) является единственной характеристикой процесса распада.
1.2 Связь скорости переходов с константами взаимодействия
Р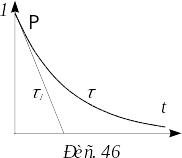 аспад
является результатом некоторого
внутреннего процесса, протекающего
внутри частицы. Скорость распада
определяется
механизмом этого процесса. Для примера
рассмотрим распад нейтрального каона:
K0-++.
Состояние
в виде нераспавшегося каона и состояние
в виде двух пионов являются начальным
и конечным состояниями одной и той же
физической системы.
Распад представляет собой переход
рассматриваемой физической системы из
одного состояния в другое. Начальное и
конечное состояния связаны между собой.
Механизм распада связывает
эти два состояния.
аспад
является результатом некоторого
внутреннего процесса, протекающего
внутри частицы. Скорость распада
определяется
механизмом этого процесса. Для примера
рассмотрим распад нейтрального каона:
K0-++.
Состояние
в виде нераспавшегося каона и состояние
в виде двух пионов являются начальным
и конечным состояниями одной и той же
физической системы.
Распад представляет собой переход
рассматриваемой физической системы из
одного состояния в другое. Начальное и
конечное состояния связаны между собой.
Механизм распада связывает
эти два состояния.
П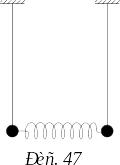 оясним
смысл понятия связи состояний с помощью
классической модели. Два совершенно
одинаковых математических маятника
при отсутствии физической связи между
ними колеблются совершенно независимо.
Если привести в движение левый маятник,
правый никак не будет откликаться. Если
же между маятниками создать механическую
связь
связать пружинкой, то при возбуждении
колебаний левого маятника, правый также
начнет раскачиваться. Движение левого
маятника затухает до полной остановки,
зато правый маятник будет при этом
совершать колебания максимальной
амплитуды. Система связанных маятников
из состояния колеблется
левый маятник
переходит в состояние колеблется
правый маятник
(в квантовой механике состояния обозначают
скобками
).
Можно говорить, что при отсутствии
пружинки между маятниками состояния
колеблется
левый маятник
и колеблется
правый маятник
не переходят друг в друга или
состояния несвязанны. При наличии
пружинки между состояниями существует
связь. Связь выражается в переходе
системы из одного в другое состояние.
Чем жестче пружинка, тем быстрее система
маятников изменяет свое состояние.
оясним
смысл понятия связи состояний с помощью
классической модели. Два совершенно
одинаковых математических маятника
при отсутствии физической связи между
ними колеблются совершенно независимо.
Если привести в движение левый маятник,
правый никак не будет откликаться. Если
же между маятниками создать механическую
связь
связать пружинкой, то при возбуждении
колебаний левого маятника, правый также
начнет раскачиваться. Движение левого
маятника затухает до полной остановки,
зато правый маятник будет при этом
совершать колебания максимальной
амплитуды. Система связанных маятников
из состояния колеблется
левый маятник
переходит в состояние колеблется
правый маятник
(в квантовой механике состояния обозначают
скобками
).
Можно говорить, что при отсутствии
пружинки между маятниками состояния
колеблется
левый маятник
и колеблется
правый маятник
не переходят друг в друга или
состояния несвязанны. При наличии
пружинки между состояниями существует
связь. Связь выражается в переходе
системы из одного в другое состояние.
Чем жестче пружинка, тем быстрее система
маятников изменяет свое состояние.
В этом же смысле понимают связь состояний K0 и -+.
Механизм связи определяет скорость перехода. Рассмотрим, чем определяется скорость перехода в системе связанных маятников. Как известно, колебание системы связанных осцилляторов представляет собой суперпозицию простых гармонических колебаний (мод). Движение системы в первой моде представляет собой колебания первого и второго маятников с одинаковыми амплитудами 01, происходящими в фазе: 1=2. Движение системы во второй моде колебания первого и второго маятников с одинаковыми амплитудами 02, происходящими в противофазе: 1=2. Каждая из мод имеет свою собственную частоту. Если колеблется только один из маятников, то это означает, что возбуждены обе моды. Движение представляет собой наложение простых синусоидальных колебаний (мод) с разными частотами. Скорость передачи колебаний от одного к другому маятнику определяется разностью частот мод. Рассмотрим это явление на примере решения задачи.
Если в начальном состоянии отклонение второго маятника равно нулю, а первого максимально, то первая и вторая моды имеют одинаковые амплитуды 01=02=0. Отклонение первого маятника 1(t) представляет собой сумму отклонений первого маятника в первой и во второй моде, т.е., равно сумме отклонений мод:
1(t)
0cos
1t+0cos
2t,
или
1(t)20cos(2-1)t/2
cos(2+1)t/2, (13)
где
0
“амплитуда” мод, 1
и
2
собственные частоты мод. При слабой
связи частоты мод отличаются мало и
12.
Отклонение первого маятника выглядит
как колебание с частотой (2+1)/2,
модулированное медленным колебанием
с частотой (2-1)/2.
Частота
модуляции
это частота перехода из состояния
колеблется
левый маятник
в состояние колеблется
правый маятник.
Она определяется устройством колебательной
системы. По сути, это не что иное, как
скорость перехода. Выразим ее через
физические параметры системы. Учтем,
что
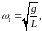
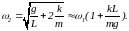 (14)
Скорость
перехода
(14)
Скорость
перехода
 ,
таким образом, равна
,
таким образом, равна
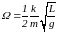 . (15)
. (15)
В рассматриваемом примере для нас сейчас важно наблюдение: скорость перехода пропорциональна жесткости связывающей пружины, то есть величине физической связи. Чем сильнее связь, тем больше скорость перехода. Отсутствие связи дает нулевую скорость перехода.
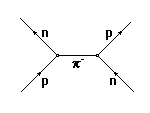
П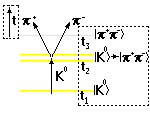 роведенное
выше рассмотрение годится как приложение
к описанию взаимодействий различного
типа. Изобразим упомянутый выше распад
нейтрального каона в виде фейнмановской
диаграммы. На этой диаграмме ось времени
идет вертикально вверх. Стрелками
изображаются изменения состояний. Если
линию мгновенного сечения пересекает
одна стрелка, то система находится в
одночастичном состоянии, если две
то в двухчастичном состоянии (обозначения,
заключенные в штриховые прямоугольники
к фейнмановской диаграмме не имеют
отношения). Физическая связь между
состояниями на диаграмме изображается
точкой, где линия каона разветвляется
на две линии пионов. В данной ситуации
физическое взаимодействие, обеспечивающее
связь между состояниями,
это слабое взаимодействие. Поэтому
говорят, что распад нейтрального каона
является слабым
распадом.
Распады почти всех нестабильных частиц,
указанных в приведенной ранее таблице,
являются слабыми. Характерные значения
времен жизни относительно этих распадов
– 10-610-14
с.
роведенное
выше рассмотрение годится как приложение
к описанию взаимодействий различного
типа. Изобразим упомянутый выше распад
нейтрального каона в виде фейнмановской
диаграммы. На этой диаграмме ось времени
идет вертикально вверх. Стрелками
изображаются изменения состояний. Если
линию мгновенного сечения пересекает
одна стрелка, то система находится в
одночастичном состоянии, если две
то в двухчастичном состоянии (обозначения,
заключенные в штриховые прямоугольники
к фейнмановской диаграмме не имеют
отношения). Физическая связь между
состояниями на диаграмме изображается
точкой, где линия каона разветвляется
на две линии пионов. В данной ситуации
физическое взаимодействие, обеспечивающее
связь между состояниями,
это слабое взаимодействие. Поэтому
говорят, что распад нейтрального каона
является слабым
распадом.
Распады почти всех нестабильных частиц,
указанных в приведенной ранее таблице,
являются слабыми. Характерные значения
времен жизни относительно этих распадов
– 10-610-14
с.
Другой пример распад нейтрального пиона на два фотона: 0+. (16) Среднее время жизни относительно этого распада равно 0,8310-16 с. Это означает, что распад происходит гораздо быстрее, чем слабый распад. Механизм связи состояний 0 и должен быть более сильным. Как показали исследования, физическим взаимодействием, результатом которого является распад нейтрального пиона, является электромагнитное взаимодействие. Времена жизни относительно электромагнитных взаимодействий лежат в области 10-1610-20 с.
Есть распады, связь между начальным и конечным состояниями в которых обеспечивается адронным взаимодействием. Например, распад -мезона. Среднее время жизни -мезона равно 4,310-24 с. Из-за того, что адронное взаимодействие является самым сильным, скорости распадов, связь в которых обеспечивается именно им, самые высокие. Характерные значения времен жизни относительно адронных распадов лежат в области 10-2110-24 с.
Задача 2. Дейтрон оказался в чистом состоянии pn. Имея в виду, что энергия связи дейтрона равна 2,2 МэВ, рассчитайте частоту переходов pnnp.
Решение. Предварительно опишем развитие аналогии. Как и у связанных маятников, равные смеси состояний pn+np и pnnp должны быть аналогичны модам колебаний маятников с определенными частотами, т.е. они должны быть состояниями с определенным значением энергии. По аналогии с механической моделью считаем, что колебание между состояниями pn и np является следствием наложения состояний с определенными значениями энергии. Далее предположим, что одно из состояний с определенным значением энергии это основное состояние, а другое несвязанное состояние, тогда энергия связи равна разности энергий состояний, аналогичных модам. Таким образом, =Eсв =Eсв/2,2710-22 с-1. (17) Это характерное значение скорости для адронного взаимодействия.
1.3 Сечение взаимодействия
Рассмотрим
еще один тип взаимодействий. Например,
при неупругом рассеянии пионов на
протонах могут рождаться лямбда-ноль
частица и ка-ноль-мезон
-+P0+K0. (18)
В
данном взаимодействии состояние -P
переходит в состояние 0K0.
Эти состояния связаны. Связь определяет
скорость перехода (вероятность перехода
в единицу времени). Как правило, такого
вида переходы описывают не скоростью,
а так называемым сечением взаимодействия.
Введение этой величины обусловлено
способом проведения эксперимента. Пучок
пионов фиксированной интенсивности I
(число
пионов, падающих на площадку единичной
площади в единицу времени) падает на
водородную мишень. Подсчитывается число
случаев NK
в
единицу времени рождения пар 0
и
K0.
Сечение
взаимодействия равно отношению этого
числа к интенсивности пучка:
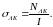 (19)
Для
придания образного смысла сечению
взаимодействия с каждым протоном можно
связать некоторый фиктивный диск, попав
пионом в который, мы добиваемся рождения
0
и
K0.
Площадь этого диска равна сечению
взаимодействия K.
(19)
Для
придания образного смысла сечению
взаимодействия с каждым протоном можно
связать некоторый фиктивный диск, попав
пионом в который, мы добиваемся рождения
0
и
K0.
Площадь этого диска равна сечению
взаимодействия K.
Рассеяние всегда происходит не на одном, а на множестве центров рассеяния. В этой ситуации формула (19) определяет полное сечение на всех центрах, расположенных в створе пучка.
Сечение
и скорость прямо пропорциональны друг
другу. Чем больше константа связи, тем
больше сечение взаимодействия. Наибольшие
значения имеют сечения адронного
взаимодействия. Следующие по порядку
величины
электромагнитные. Наименьшие значения
имеют сечения слабых процессов (например,
рассеяние нейтрино на протонах). На
схеме в логарифмическом масштабе
показаны интервалы возможных значений
сечений рассеяния.
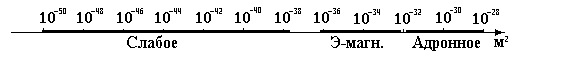
Единицами измерения сечений являются м2, барн (б) (1 (б)=10-28 м2) и фм2=10-30 м2 (фм ферми, или фемтометр, равный 10-15 м).
