1.4 Упражнения для самостоятельной работы

Задача 5. Определите, какие взаимодействия могут идти, а какие  нет. Почему? 1. e^+e^ ; 2. K^+P ^+ ^; ^3. K^+P ^+ ^; ^4. K^+P^ +^; 5. ^+P^ +^; ^6. ^+P^ +K^; ^7. K^+P^+^; 8. K^+PP+K^ +^; ^9. K^+PP +^; 10. _ +Pn+^; 11. 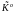+ P^ +^; ^12. +PK^+P +^;

Задача 6. При рассеянии нейтрино высокой энергии, получающихся при распаде пионов на лету по схеме на протонах рождаются две частицы. Одна из них нейтрон. а) Какая вторая частица? б) Какой результат этого эксперимента подтверждает закон сохранения лептонного числа? в) Следует ли из данного эксперимента, что электронное и мюонное нейтрино являются разными частицами?

Задача 7. При рассеянии фотонов подходящей энергии на атомах возможно поглощение атомом фотона и переход атома в возбужденное состояние. Аналогичное явление наблюдается при рассеянии фотонов на протонах: фотон поглощается, а протон переходит в возбужденное состояние, превращаясь в -резонанс. О чем говорит тот факт, что такое никогда не происходит при рассеянии фотонов на электронах?

2. Домашнее задание

2.2 Решение задач

Задача 1. Возможны ли следующие взаимодействия: 1. K^+PP+K^+^+^+^ ^2. K^+P K^+ P+^ ^3. K^+P K^+P+^ 4. P+P^+ e^+e^ ^5. P+P^+P+e^+_e 6. _e+PK^+e^+^ ^7. e^+e^ P+  ^8. ^^+ +_

Обменное взаимодействие

1. Повторение принципа неопределенностей

1.1 Неопределенность координаты и импульса

Ц ентральными в квантовой механике являются понятие амплитуды вероятности и принцип суперпозиции состояний. Описание состояний частиц с помощью амплитуд вероятности говорит о том, что в каждый момент времени точечная частица занимает сразу некоторую область пространства. Связанное состояние частицы описывается локализованным в ограниченной области пространства распределением амплитуд вероятности. Такому распределению отвечает некоторый размер области локализации x.

Частица, находящаяся в локализованном состоянии, не имеет определенного значения импульса. Если проводить измерения импульса локализованной частицы, результатами эксперимента будут являться случайные значения, распределенные около нуля. Разброс измеряемых значений импульса P_x тем больше, чем в меньшей области локализовано распределение амплитуды вероятности. В этом состоит принцип неопределенностей. На рисунке 44 изображены графики распределений вероятности координаты частицы (ввер­ху) и значений импульса в том же состоянии (внизу). Математическое выражение принципа имеет вид P_x x~ћ/2. (1)

Из принципа неопределенности в частности следует, что для того, чтобы локализовать положение частицы, надо совершить работу.

Задача 1. Частица массы m находится в непроницаемом ящике размером L, с подвижной стенкой. Используя принцип неопределенностей оцените увеличение энергии частицы при уменьшении размера ящика путем перемещения подвижной стенки на dL. Используя полученный результат, найдите силу, с которой частица действует на стенку.

Локализованная частица создает давление на тела, которые ограничивают область расположения частицы (гайзенберговское давление). В атоме электронное давление компенсируется силой притяжения к ядру. В ядре из-за сильной локализации нуклонов гайзенберговское давление чрезвычайно велико, поэтому только мощное адронное притяжение способно удерживать его от разрыва.

Задача 2. На малых расстояниях ядерное притяжение гораздо сильнее электростатического притяжения разноименно заряженных частиц. Объясните кажущийся парадокс: почему слабое электростатическое притяжение удерживает электрон около протона в атоме водорода, а более сильное ядерное притяжение не способно удержать вместе два нейтрона.