
- •Введение
- •Содержание разделов дисциплины
- •Раздел I. Число. Числовая последовательность
- •Раздел II. Числовая функция. Предел и непрерывность функции
- •Раздел III. Дифференциальное исчисление функции одной переменной
- •Раздел IV. Интегральное исчисление функций одной переменной
- •I Действительные числа
- •II Функции действительного переменного
- •III Предел функции
- •IV Непрерывность функции
- •V Дифференцирование функции
- •VI Исследование поведения функции и построение ее графика
- •VII Наибольшее и наименьшее значение функций
- •VIII Неопределенный интеграл
- •IX Определенный интеграл
- •Учебная литература по курсу
VIII Неопределенный интеграл
Определение 8.1
Функция
![]() называется первообразной для функции
на интервале (а, b),
называется первообразной для функции
на интервале (а, b),
Если
для всех ![]() имеет место соотношение
имеет место соотношение ![]() .
.
Очевидно,
что вместе с функцией
первообразной для
будет и функция ![]() ,
где С – произвольное постоянное число.
Совокупность всех первообразных
для функции
называется неопределенном интегралом
и обозначается:
,
где С – произвольное постоянное число.
Совокупность всех первообразных
для функции
называется неопределенном интегралом
и обозначается:
![]() (8.1)
(8.1)
Отметим,
что интегрирование (то есть нахождение
первообразной для
)
является обратной операцией к
дифференцированию (то есть нахождению
производной для функции ![]() Отсюда вытекают простейшие свойства
неопределенного интеграла:
Отсюда вытекают простейшие свойства
неопределенного интеграла:
а также таблица неопределенных интегралов для элементарных функций:
 , если
, если









Искусство интегрирования состоит в том, чтобы интеграл от произвольной функции свести к одному или нескольким табличным интегралам 1) – 9). Существует несколько стандартных приемов (методов), позволяющих это сделать.
Метод замены переменной основан на формуле
![]() =
=![]() (8.3)
(8.3)
и при удачном выборе функции позволяет получить в правой части формулы (8.3) один из табличных интегралов.
Дадим несколько полезных советов, которые можно использовать при использовании формулы.
Замена
 ,
,
 ,
, 


 ,
,








 ,
, 

 ,
, 

 ,
, 

 ,
, 
Пример
![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() + C
=
+
+ C
=
+ ![]() + C
+ C
Замена
Метод интегрирования по частям основан на формуле
![]() (8.4)
(8.4)
которая легко получается из правила дифференцирования произведения двух функций:
![]() .
Первообразной для функции
.
Первообразной для функции ![]() является, очевидно, функция
является, очевидно, функция
![]() ,
а первообразная для функции
,
а первообразная для функции ![]() равна
равна ![]() +
+ ![]() , так что получим
, так что получим
= + (8.5)
отсюда и следует формула (8.4). Предполагается, что в формуле (8.4) интеграл, стоящий в правой части равенства вычисляется проще, чем интеграл, стоящий в левой части равенства.
Пример 1
Вычислить
интеграл ![]() .
Обозначим
.
Обозначим ![]() =
=
![]() .
Согласно (8.4) получим:
.
Согласно (8.4) получим:
= - ![]() =
= ![]()
Пример 2
Вычислить
интеграл ![]() .
Обозначим
.
Обозначим ![]() =
=
![]() .
Согласно (8.4) получим:
.
Согласно (8.4) получим:
= (![]()
![]() –
– ![]()
![]() (
-
= (
-
(
-
= (
- ![]()
IX Определенный интеграл
Понятие
определенного интеграла возникло в
связи следующей конкретной задачей.
Пусть на отрезке [a,b]
задана непрерывная функция
=
,
такая что
> 0 для ![]() a,b].
Требуется определить площадь
криволинейной фигуры
a,b].
Требуется определить площадь
криволинейной фигуры ![]() ,
ограниченной осью О
,
прямыми
,
ограниченной осью О
,
прямыми ![]() и графиком функции
=
(см. рис 9.1).
и графиком функции
=
(см. рис 9.1).
Чтобы
подсчитать площадь
,
делят отрезок [a,b]
на
(необязательно равных) частей
![]() ,
,![]() ],
],![]() ,
,![]() ],
,
],
, ![]() ,
,![]() ],
где
],
где ![]() . На каждом отрезке
. На каждом отрезке ![]() ,
,![]() ]
выбирают точку
и подсчитывают площадь прямоугольника
с длиной основания
]
выбирают точку
и подсчитывают площадь прямоугольника
с длиной основания ![]() и высотой
и высотой ![]() .
.
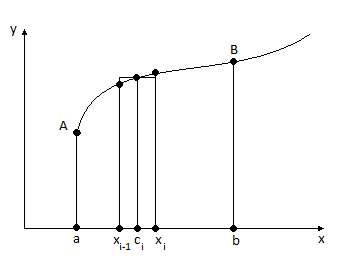
Тогда
сумма ![]() будет приближенно равна искомой площади
.
С увеличением числа отрезков
(и уменьшение их длин) точность подсчета
площади
возрастает. Сумма
будет приближенно равна искомой площади
.
С увеличением числа отрезков
(и уменьшение их длин) точность подсчета
площади
возрастает. Сумма ![]() называется интегральной
суммой для
функции
на отрезке [a,b].
называется интегральной
суммой для
функции
на отрезке [a,b].
Определение 9.1
Предел
интегральной суммы для функции
на отрезке [a,b]
при![]() ( при max
( при max
![]()
![]() ) называется определенным интегралом
от функции
на отрезке [a,b]
и обозначается:
) называется определенным интегралом
от функции
на отрезке [a,b]
и обозначается:
![]() =
= ![]() (9.1)
(9.1)
Функция в этом случае называется интегрируемой на отрезке [a,b].
Из определения (9.1) легко вытекают следующие его свойства:
а)
![]()
б)
![]()
![]()
в)
![]()
г)
![]()
д)
![]()
е)
![]()
![]()
Важное значение также имеет теорема о среднем значении, которую мы приведем без доказательства.
Теорема 9.1
Если
функция ![]() непрерывна на отрезке [a,b],
то она интегрируема на этом отрезке,
причем обязательно найдется такая точка
непрерывна на отрезке [a,b],
то она интегрируема на этом отрезке,
причем обязательно найдется такая точка
![]() [a,b],
что будет справедливо соотношение:
[a,b],
что будет справедливо соотношение:
![]() (9.2)
(9.2)
Геометрически
утверждение теоремы 9.1 означает, что
площадь криволинейной фигуры
(рис.9.1) будет равна площади прямоугольника
с длиной основания ![]() и высотой, равной значению
и высотой, равной значению ![]() в некоторой точке
[a,b].
в некоторой точке
[a,b].
Очевидно, что определение 9.1 не дает простого эффективного правила для вычисления определенного интеграла. Такое правило дает
Теорема 9.2
Пусть функция непрерывна не некотором интервале, включающем отрезок [a,b] и - любая ее производная. Тогда справедлива формула Ньютона-Лейбница:
![]() (9.3)
(9.3)
Доказательство.
Возьмем
некоторую точку ![]() и рассмотрим интеграл
и рассмотрим интеграл ![]() .
Очевидно, значение этого интеграла
зависит от выбора точки
,
поэтому мы имеет некоторую функцию
.
Очевидно, значение этого интеграла
зависит от выбора точки
,
поэтому мы имеет некоторую функцию ![]() ,
определенную на отрезке [a,b].
Дадим аргументу
приращение
и рассмотрим соответствующее приращение
функции
,
определенную на отрезке [a,b].
Дадим аргументу
приращение
и рассмотрим соответствующее приращение
функции ![]() .
Так как по свойству е)
.
Так как по свойству е) ![]() ,
то
,
то ![]() .
Далее, поскольку функция
непрерывна на отрезке [a,b],
то по теореме 9.1 будем иметь
.
Далее, поскольку функция
непрерывна на отрезке [a,b],
то по теореме 9.1 будем иметь ![]() Тогда
Тогда ![]() и перейдя в этом соотношении к пределу
при
и перейдя в этом соотношении к пределу
при ![]() мы получим,
мы получим, ![]() =
=
![]() .
Это означает, что производная от функции
.
Это означает, что производная от функции
![]() в любой точке
в любой точке ![]() [a,b]
совпадает со значением функции
,
то есть
- одна из первообразных для функции
на отрезке [a,b].
Пусть
[a,b]
совпадает со значением функции
,
то есть
- одна из первообразных для функции
на отрезке [a,b].
Пусть ![]() - любая первообразная для функции
,
тогда
- любая первообразная для функции
,
тогда ![]() ,
то есть
,
то есть ![]() для любого
[a,b].
Если взять значение
для любого
[a,b].
Если взять значение ![]() ,
то получим
,
то получим ![]() взять значение
взять значение ![]() , то получим
, то получим ![]() , что и требовалось доказать.
, что и требовалось доказать.
Приложение определенного интеграла
Вычисление площади плоской фигуры
Пусть плоская фигура ограничена кривыми =
 ,
=
,
=  и прямыми линиями
, то площадь вычисляется по формуле
и прямыми линиями
, то площадь вычисляется по формуле
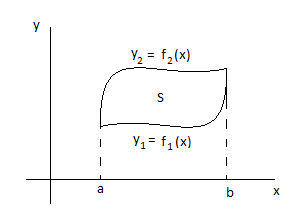
![]()
Пусть плоская фигура ограничена кривыми = , =
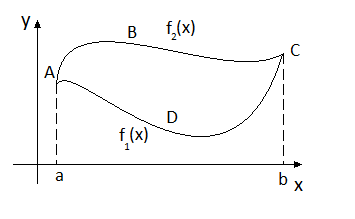
Найдем сначала точки пересечения кривых, решив уравнение
![]()
Представим плоскую фигуру как разность двух криволинейных трапеций:
![]() и
и ![]() тогда искомая площадь
тогда искомая площадь ![]() исходя из геометрического смысла
определенного интеграла равна разности
площадей указанных трапеций
исходя из геометрического смысла
определенного интеграла равна разности
площадей указанных трапеций
![]()
Пример
Вычислить площадь фигуры, ограниченной линиями
![]() ,
, ![]()
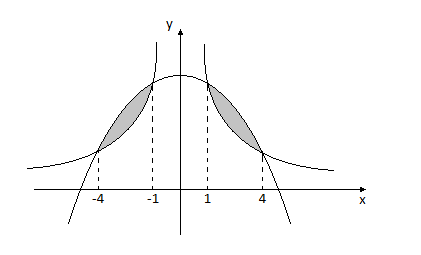
![]()
![]()
![]()
![]() ,
, ![]()
![]()
Вычислить интегралы






















 на [
на [ ]
функции
]
функции 
а)
![]() ,
если
,
если ![]() - четная функции
- четная функции
б)
![]() ,
если
- нечетная функции
,
если
- нечетная функции
