V Дифференцирование функции
Производная и ее свойства
Пусть
задана функция 
на
некотором интервале (а,b).
Возьмем любую точку 
(а,b)
и придадим аргументу
некоторое
приращение 
,
так чтобы точка 
(а,b)
Тогда и функция получит приращение
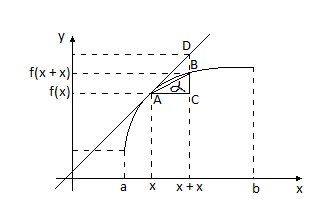
Рис. 5.1
Определение 5.1
Производной
функции 
в точке
называется конечной предел при 
отношения приращения функции к приращению
аргумента, то есть
, или 
Для
обозначения производной используются
символы: 
,
,
.
Геометрически
производная функции
в точке
означает
тангенс угла наклона касательной к
графику функции в точке 
по отношению в оси О
(см. рис.5.1).
Действительно,
отношение 
равно тангенсу угла
между хордой АВ и отрезком АС, но при
стремлении
к нулю точка В, двигаясь вдоль кривой,
приближается к точке А и предельное
положение хорды АВ и будет совпадать с
положением касательной к графику функции
в точке
.
Для
разъяснения физического (механического)
смысла производной рассмотрим конкретную
функцию 
,
где 
означает пройденный путь к моменту
времени 
.
Задавая приращение времени 
,
мы получим приращение пути 
.
Очевидно, отношение
представляя собой среднюю скорость
движения на промежутке времени [
].
Тогда 
обозначает мгновенную скорость движения
в момент времени
.
Распространяя физический смысл
производной на случай произвольной
функции, можно сказать, что производная
означает скорость изменения функции
в
точке
.
Теорема 5.1
Если функция = имеет в точке производную , то она в этой точке непрерывна.
Действительно,
(5.1)
+ 
,
где
- бесконечно малая функция (5.2)
Откуда
+ 
(5.3)
устремим
,
тогда 
, то есть выполняется определение (4.2)
Следствие
Если функция = имеет производную в каждой точке интервала (а, b), то она на этом интервале непрерывна.
Определение 5.2
Говорят,
что функция
=
имеет в точке
максимум (минимум), если для всех значений
из некоторой окрестности (
)
(
)
точки
выполняется неравенство 
Теорема 5.2
Пусть
функция
=
определена на интервале (а, b)
и в точке 
имеет производную. Тогда если
> 0 (
< 0), то функция возрастает (убывает) в
некоторой окрестности (
)
точки 
Рассмотрим случай, когда > 0 (случай < 0 рассматривается аналогично).
Возьмем
число
так, чтобы 
/ 2 . Тогда согласно определению производной
найдется такое
, что как только |
| < 
,
то | 
|
<
. Как мы знаем, последнее неравенство
можно представить в виде
-
< 
-
<
(5.3)
- < < + (5.4)
Из двух неравенств (5.4) мы рассмотрим подробно первое неравенство. Имея в виду, что < / 2 получим неравенство:
> 
> 0 (5.5)
которое
выполняется для всех
,
если |
<
. Если при этом
(
) (то есть
> 0 ), то 
;
если же
(
) (то есть этом
< 0 ), то 
. А это и означает, что в окрестности
(
)
точки
функция
=
возрастает, то есть 
> 
, если 
.
Следствие. Если функция = имеет в точке экстремум (то есть максимум или минимум) и в этой точке существует производная, то она равна нулю, то есть = 0 .
Действительно,
если предположить, что
,
по теореме 5.2 функция
=
будет в окрестности точки
либо возрастать, либо убывать, что
противоречит определению 5.2.
Теорема 5.3
(Производная
от обратной функции.) Если функция
=
имеет в точке
производную
, то обратная функция 
имеет в точке 
=
производную причем 
= 
(5.6)
Дадим
аргументу
приращение
в
точке
, тогда функция
=
получит приращение 
(так как
).
Тогда можно записать
(5.7)
Переходя
в равенстве (5.7) к пределу при
(при этом также и
по непрерывности функции
= 
получим формулу (5.6)
Теорема 5.4
(Производная
от сложной функции). Если функция 
имеет производную в точке 
,
а функция
=
имеет производную в точке 
,
то сложная функция 
имеет производную в точке
,
при чем
=
* 
(5.8)
Действительно,
задав приращение 
аргументу 
,
мы получим приращение
= 
- 
, но приращению
будет соответствовать приращение
= 
=
.
Тогда
= 
= 
=
*
Теорема 5.5
(Арифметические
свойства производных). Пусть функции
и 
имеют производные на интервале
(а,b),
тогда функции 
+
*
и 
(в
последнем случае на интервале (а,b))
тоже имеют производные, причем
справедливы следующие отношения:
=
+ 
=
=
= 
Докажем соотношение 3). По определению производной получаем:
= 
= 
= 
+ 
=
Производные элементарных функций
а) Производная от линейной функции равна ее угловому коэффициенту.
Действительно
= 
= 
= 
В
частности, отсюда следует, что производная
от постоянной равна нулю.
б)
Производная от степенной функции 
выражается формулой
= 
(5.10)
Формулу (5.10) для натуральных значений можно доказать методом математической индукции. Справедливость ее для = 1 следует из предыдущего пункта а). Предположим, что формула (5.10) верна для некоторого натурального числа и докажем, что тогда она верна и для ( + 1). Действительно, используя арифметическое свойство производных (формула 5.9 в)), получим:
= 
=
= 
+ 
= (
+ 1)
в) Производные тригонометрических функций выражаются формулами:
= 
= - 
= 
= 
(5.11)
Докажем первую из этих формул (для второй это делается аналогично, а третья и четвертая формулы следуют из свойства 5.9 г)). По определению производной имеем:
= 
=
Здесь
мы используем первый замечательный
предел 
= 1 и непрерывность функции 
: 
=
г) Производная от натурального логарифма выражается формулой:
= 
(5.12)
По определению предела будем иметь:
= 
=
ln
=
ln
Обозначая
, 
= 
ln
= 
ln
=
Так
как 
= 
, то 
= 
д) Производная от показательной функции выражается формулой:
= 
(5.14)
Дифференциал функций
Определение 5.3
Дифференциалом
функции
=
в точке
называется произведение производной
в этой точке на приращение аргумента,
то есть
(5.19)
Для
простейшей линейной функции
=
дифференциал 
,
поэтому формулу (5.19) записывают также
в виде:
(5.20)
Из
формулы (5.20) следует и другое обозначение
для производной 
Используя рис. 5.1, мы можем установить
геометрический смысл дифференциала.
Так как производная
равна 
,
из треугольника 
следует, что
= 
,
то есть дифференциал функции
=
в точке
равен приращению линейной функции с
угловым коэффициентом
.
При достаточно малых
дифференциал функции примерно равен
ее приращению, поэтому дифференциал
функции можно использовать для
приближенных вычислений, используя
формулу (см.рис. 5.1)
(5.21)
Приведем примеры применения формулы (5.21)
Приближенно вычислить
,
при 
Возьмем
,
= 
Приближенно вычислить
при
Возьмем
,
