2. Ковариантная производная вектора[2, 3]

Для изучения локальных свойств векторных полей необходимо знать изменение этих полей при бесконечно малом изменении положения точки в пространстве. При рассмотрении векторных полей в криволинейных координатах сложность определения дифференциальных свойств векторных полей связана с тем, что векторы локального базиса изменяются при изменении положения точки пространства.

Рассмотрим частные производные от векторов , локального базиса . Эти величины являются векторами (как предел разности двух векторов, умноженных на скаляр при ), поэтому их можно разложить по векторам локального базиса

. (30)

Коэффициенты разложения (координаты вектора в базисе ) называются символами Кристоффеля 2-го рода. По определению и, следовательно,

. (31)

Из сравнения выражений (30) и (31), а также в силу единственности определения координат вектора получаем, что , т.е. символы Кристоффеля симметричны по нижним индексам.

Символы Кристоффеля можно найти, зная коэффициенты метрического тензора. Действительно,

.

Подставляя в правую часть этого равенства выражение (30), получим

или окончательно

(32)

Меняя последовательно местами (т.е. на , а на ) и в равенстве (32), получим

(33)

(34)

Складывая равенства (33) и (34), вычитая равенство (32) и учитывая симметрию по нижним индексам, находим

(35)

Умножая левую и правую части (35) на и суммируя по , получим

. (36)

Рассмотрим векторное поле , заданное своими координатами, функциями , , в прямоугольной декартовой системе координат. Частные производные этого поля по координатам имеют вид

,

т.е. компоненты вектора получаются частным дифференцированием соответствующей компоненты вектора.

В криволинейной системе координат

,

где − координаты вектора в локальном базисе .(В соответствии с ранее принятым соглашением волна над координатами опущена). Заменяя индекс суммирования на в первом слагаемом правой части последнего выражения (индекс суммирования мы можем обозначать любой буквой), получим

, (37)

где обозначено

. (38)

В выражениях (37) и (38) использовано обозначение с запятой, чтобы подчеркнуть, что индекс связан с дифференцированием по координате . Величина называется ковариантной производной контрвариантных компонент вектора и является тензором (точнее координатами некоторого тензора).

По аналогии определим ковариантную производную ковариантных компонент вектора с помощью формального равенства

(39)

Умножая левую и правую части этого равенства скалярно на получим

(40)

Получим выражение для . Умножим равенство скалярно на , получим

.

Продифференцировав это равенство частным образом по , находим

(41)

Подставляя в (41) выражения (39) и (30), получаем

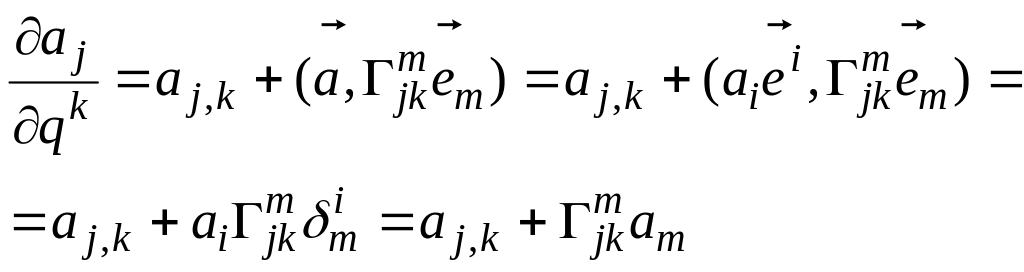
Откуда следует

. (42)

С помощью выражений (39) и (42) для векторов , получаем

(43)

Можно показать, что для ковариантных производных и справедливы формулы «жонглирования»

.