7.3. Принцип максимума л.С. Понтрягина

Принципу максимума Л.С. Понтрягина можно дать следующую геометрическую интерпретацию (рис. 7.1). Пусть стоит задача о переводе за максимальное время изображающей точки из некоторого начального положения 0 в конечное положение К. Каждой точке фазового пространства, окружающей точку К, соответствует определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг конечной точки можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем перехода в эту точку. Такие поверхности называются изохронами. Очевидно, что оптимальная по быстродействию траектория из точки 0 в конечную точку К должна быть максимально близка нормалям к изохронам, насколько это позволяют ограничения на координаты объекта управления.

Действительно, всякое движение вдоль изохрон увеличивает время процесса, так как означает затрату времени без уменьшения отрезка времени, остающегося до момента достижения конечной точки. Математически это условие оптимальности траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально. (Скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними).

Если обозначить это произведение через Н, а вектор, обратный градиенту времени перехода, через , т.е. (рис. 7.1), то это условие можно записать следующим образом

, (7.19)

где – координаты вектора и , т.е. условием оптимальности является максимум проекции вектора на направление .

Сформулированное условие оптимальности и есть принцип максимума Л.С. Понтрягина.

Допустим, что уравнение динамики САУ заданы в следующей общей форме

; (7.20)

– переменные, относящиеся к заданной части системы, включающей в себя регулируемый объект и не изменяемую в процессе синтеза часть регулятора;

– переменные, выражающие воздействие проектируемой части САУ на заданную часть системы и называемые управляемыми. Неизменной частью САУ может быть, например, исполнительный привод, тогда будут воздействиями измерительно-преобразовательной части САУ на его силовую часть (рис. 7.2).

В рассматриваемом случае необходимо найти управления в виде

. (7.21)

Во всякой реальной системе величины управлений будут иметь ограничения, например , или любые другие, определенные областью допустимых значений.

Критерием оптимальности системы пусть будет минимум некоторого функционала

. (7.22)

Для удобства решения задачи вводится дополнительная искусственная переменная х₀ (t), определяемая уравнением

, (7.23)

а также вспомогательные переменные , определяемые линейными однородными уравнениями вида

; (7.24)

.

Если теперь ввести вспомогательную функцию Н в виде

(7.25)

то все уравнения (7.20), (7.23), (7.24) можно объединить в одну систему типа известной из механики системы уравнений Гамильтона, а именно:

(7.26)

Принцип максимума гласит, что для оптимальности системы, т.е. для получения минимума функционала I (7.22), необходимо существование таких нулевых функций , что при любом t, находящемся в заданном интервале , величина Н, как функция переменных в заданной области их допустимых значений достигает максимума

, (7.27)

причем и М постоянны во времени и при

Для оптимальности по быстродействию имеем , а функция Н принимает вид

(7.28)

где .

В этом случае Гамильтонова система уравнений принимает вид

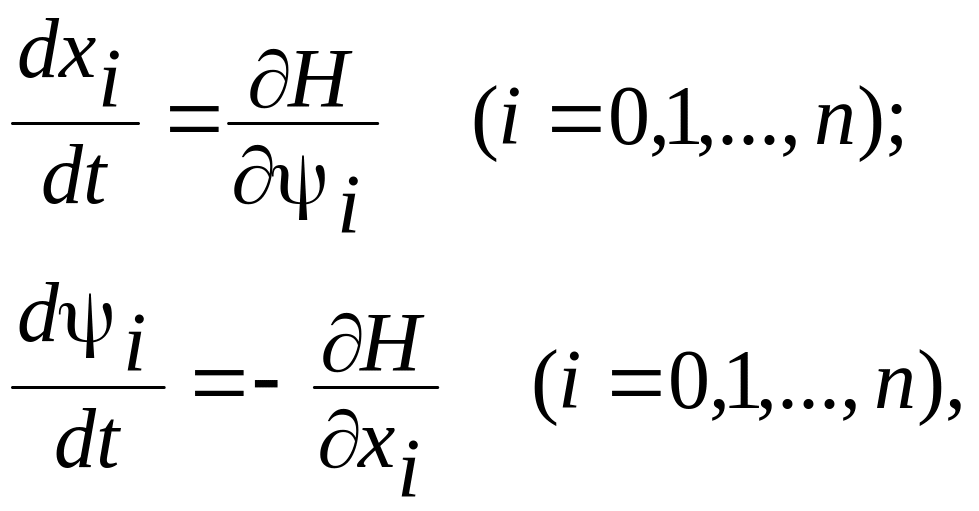(7.29)

а принцип максимума будет следующим. Для оптимальности системы по быстродействию необходимо существование таких ненулевых непрерывных функций , что для всех t в заданном интервале функция Н переменных в заданной области их допустимых значений достигает максимума

, (7.30)

причем М постоянна во времени .

Согласно проведенным формулировкам принцип максимума дает только необходимые условия оптимальности. Вопрос же о существовании ее и о случаях достаточности этих условий очень труден. Поэтому в практических приложениях предполагают достаточность по физическому смыслу исследуемой системы.

Пример. Система задана уравнением:

(7.31)

Требуется найти управление , чтобы система была оптимальной по быстродействию при переходе ее из произвольного начального состояния в равновесное состояние .

При этом на управление наложено ограничение .

Обозначив , приведем уравнение (7.31) к исходному виду (7.20):

(7.32)

Функция Н согласно (7.28) будет иметь

(7.33)

Чтобы определить максимум Н по переменной , надо найти . Для этого воспользуемся уравнениями (7.29), которые в данном случае будут иметь вид

оттуда .

Принцип максимума (7.30) с учетом выражения (7.33) и ограничения дает

, (7.34)

так как положительный максимум функции Н по переменной будет согласно (7.33) при , когда и при , когда .

Поскольку линейная функция не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с на или наоборот.

Следовательно, оптимальная по быстродействию система будет релейной, но не обычной релейной, а с особым специальным законом переключения реле по знаку вспомогательной функции . Чтобы представить себе это нагляднее, изобразим процесс на фазовой плоскости.

Исключив из уравнения (7.32) , получим при дифференциальное уравнение , оттуда фазовая траектория будет

(7.35)

Аналогично, при

(7.36)

Это параболы, симметричные относительно оси абсцисс .

Процесс должен заканчиваться в начале координат .

Поэтому в начале изобразим фазовые траектории (параболы), вливающиеся в начало координат соответственно при и при , как показано сплошными линиями на рис. 7.3.

Нанесем теперь и все остальные параболы с различными значениями с в формулах (7.35 и 7.36) до точек их вливания в изображенные ранее две ветви параболы, идущие к началу координат (рис. 7.4).

Как видим, из произвольной точки процесс идет по некоторой параболе М₀D при управляющем сигнале (в другой области было бы ). В точке D происходит переключение реле на сигнал , после чего процесс идет по параболе D0 и заканчивается в точке 0 за конечное время, которое согласно принципу максимума является минимальным из всех возможных для перехода данной системы из состояния , в равновесное состояние 0 (0, 0).

Точка переключения реле D может находиться в любом месте кривой А0В. Последняя поэтому называется линией переключения. На ней лежат заключительные отрезки фазовых траекторий, приходящие в начало координат.

Итак, искомое уравнение преобразовательной части системы (оптимальной по быстродействию будет

(7.37)

причем отсчитывается на оси абсцисс. Замечая, что , из формул (7.35), (7.36) и рис. 7.4 находим уравнение линии переключения

(7.38)

и, следовательно, уравнение преобразовательной части системы будет

(7.39)

Это значит, что в системе должно быть два измерителя (для и для ), либо один измеритель и дифференцирующее устройство. Переключающее значение должно формироваться (автоматически вычисляться) согласно формуле (7.38), и на основе сравнения фактического текущего значения со значением , зависящего от текущего , должно производиться включение и переключение реле в соответствии с уравнением (7.39).

Это является специальным нелинейным законом управления для линейного объекта, приводящим к оптимальной по быстродействию системе.

299