33.Переходный процесс эл. привода с линейной хар-ой при одно- и многоступенчатом пуске при ω₀=const, M_C=const.

При одноступенчатом пуске переходный процесс описывается уравнениями

;

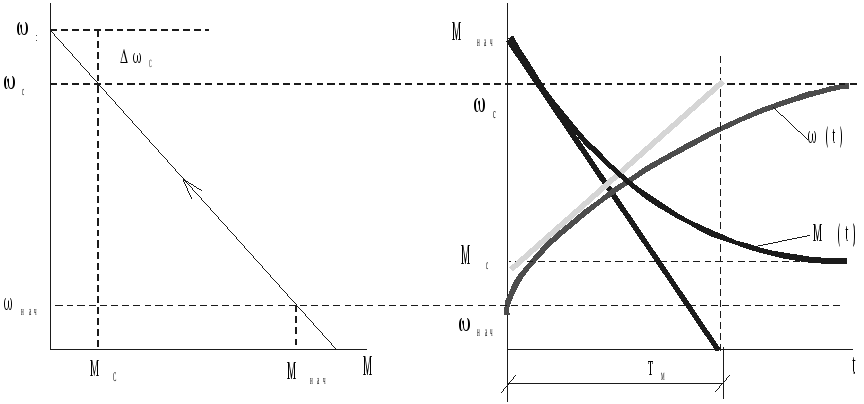
если увеличение скорости происходит не от=0, а от какого-то начального установившегося значения, как показано на графиках.

Закон изменения ускорения , где

Уменьшение ε по мере увеличения скорости объясняется непрерывным уменьшением динамического момента М_дин. Если разгон идет из

Законы изменения и М при разгоне на любой ступени определяются согласно ранее приведенным выражениям.

Для примера рассчитаем переходный процесс на первой и второй ступенях. Сначала для первой ступени

1. 3.

2. 4.

Значения _н1 и _с1 находятся из графика, где изображена пусковая диаграмма при М=М_н и М=М_с . Задаваясь временем t от 0 до t₁ , рассчитываются законы изменения и М на первой ступени и строятся кривые =f(t) и M=f(t).

Далее делается расчет процесса на второй ступени

1. 3.

2. 4.

Значения _с2 и _к1 находятся из пусковой диаграммы. Задаваясь временем t от 0 до t₂, рассчитываются и строятся кривые =f(t) и M=f(t) для второй ступени и т.д. Время разгона на естественной характеристике до =_н=_с принимается равным t_н=(3-4)T_м, где в Т_м вместо _нх подставляется _н.

34. Переходные процессы эл. привода с линейной хар-ой при ω₀=const, M_C=const в тормозных режимах.

Рассмотрим сначала реверс, который заключается в торможении противовключением с дальнейшим изменением направления вращения и разгоне в противоположную сторону.

Если реверс осуществляется при активном моменте сопротивления М_с=const, переходный процесс описывается уравнениями, приведенными ранее для двигательного режима, с той разницей, что в выражениях для ω и М нужно поставить знак минус перед ω_с и перед М_нач

На графике с механическими характеристиками показан переход из двигательного режима в режим противовключения и построены кривые переходного процесса. Двигатель при переводе егов режим противовключения тормозится по линии ВС. Затем, если его не отключить от сети, будет разгоняться в обратном направлении по линии

Дин. торможения и вертикали М_c =const. В случае активного М_с точка “B”, соответствующая ω_с2, относится к случаю, когда этот момент в начале процесса является тормозным, что действует при подъеме груза, а т. “c” с установившейся скоростью ω_с1- к случаю, когда этот момент является движущим при спуске груза (рис.а). В случае торможения при подъеме груза под действием М_с и тормозного момента двигателя привод вначале будет тормозится и остановится, т.к. момент двигателя станет =0, но т.к. М_с является активным и будет продолжать действовать в том же направлении, под его действием система будет вращаться в обратную сторону. При этом М_с из момента сопротивления (тормозного) превратится в движущий, а тормозной момент двигателя изменит свой знак и будет продолжать действовать как тормозной. Установившаяся скорость наступит при равенстве момента двигателя и М_с т.е. в т. В. Кривые переходного процесса этого случая изображены на рис. “б”. Время торможения до ω=0 , т.е. до остановки

Если активный момент сопротивления в начале торможения был движущим (торможение при спуске груза ), то в начале торможения тормозной момент (отрезок ED на рис.”а”) больше движущего статического момента и есть замедление, сопровождающееся уменьшением тормозного момента двигателя. При скорости ω_с1 M=M_c, замедление прекращается и наступает установив-шийся режим тормозного спуска груза со скоростью ω_с1. В этом случае затормозить систему до остановки путем динамического торможения нельзя (рис.”в”). При реактивном моменте сопротивления динамическое торможение происходит так же, как и при подъеме груза. Разница лишь в том, что

36. Переходный процесс эл. привода с линейной хар-ой при ω₀=f(t), M_C=const в тормозных режимах.

При пуске электропривода включением его в сеть на полное напряжение U=const и f₁=const переходные процессы протекают при скачке напряжения, или как говорят, скачке управляющего воздействия, когда ₀=const. Для ограничения бросков тока и момента в якорную или роторную цепь двигателя приходится вводить добавочное сопротивление. Переходные процессы при этом будут далеки от оптимальных. При питании двигателя от преобразователя напряжения или частоты ( в замкнутых системах) можно получить переходные процессы, близкие к оптимальным, путем плавного изменения управляющего воздействия. Они протекают в этом случае при ω₀=f(t). При этом ограничивается темп нарастания управляющего воздействия путем ограничения ускорения ω ₀ Т.о. переходные процессы протекают в этом случае при U=var или f=var.

Проанализируем переходные процессы при линейном изменении управляющего воздействия ω _0 во времени, т.е. при линейном изменении U или f₁, при котором ω ₀= ω _{0 нач}+εt.

Исходными дифференциальными уравнениями для получения расчетных соотношений являются ранее полученные уравнения

При соотношении постоянных времени величиной Т_э можно пренебречь и уравнение, определяющее закон изменения ω будет иметь вид

Правая часть этого уравнения – частное решение, соответствующее установившемуся режиму, когда все свободные составляющие затухнут. Для этого режима ω =a+bt, где а и b – неопределенные коэффициенты , находимые из начальных условий. Имея в виду, что , получим приt=0

Отсюда

Общее решение дифференциального уравнения относительно ω

37.Переходный процесс электропривода с двигателем независимого возбуждения при из­менении магнитного потока

Обычно ДНВ работает при Ф=Ф_н если U=const или U=var. Необходимость ослабления по­тока возникает когда требуется получить скорость, превышающую основную (согласно тре­бованиям технологического процесса ). Если бы поток изменялся мгновенно, то в началь­ный момент времени имел бы место бросок тока и момента, как показано на рисунках ω=f(I_a) и ω =f(M) пунктиром . В действительности Ф изменяется во времени. Поэтому ток якоря и момент двигателя будут изменяться по т.н. динамическим характеристикам (кривая1). Для расчета переходного процесса пренебрегаем индуктивностью якоря L_Я т.к. она мала по сравнению с индуктивностью L_В обмотки возбуждения. Бросок тока и момента будет тем больше, чем быстрее темп изменения Ф. Для получения расчетного выражения воспользуемся уравнением равновесия ЭДС в якорной цепи и уравнением момента.

Выразим коэффициенты “k” через номинальные параметры. Коэффициенты ЭДС

;

1) ; 2)

Определив из второго уравнения I_Я и подставив в первое, а также разделив полученное выражение на , получимили в относительных единицах

3) , где;

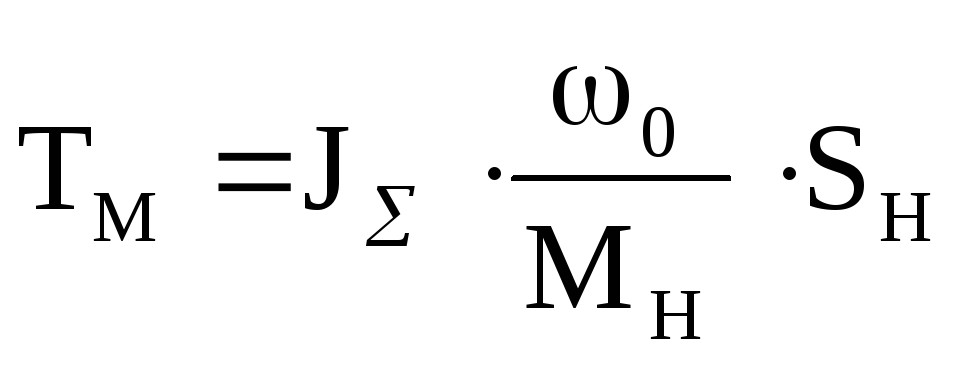
Это уравнение нелинейное и решить его непосредственно нельзя, т.к. φ =f(t). При небольших пределах изменения Фможно считать, что Физменяется по линейному закону, как показано на графике кривой намагничивания. Линейное изменение потока имеет место в случае, если , т.е. когда цепь машины не насыщена (здесь допускается некоторая погрешность). Закон изменения тока возбуждения при ненасыщенной магнитной цепи можно найти из уравнения равновесия ЭДС для цепи возбуждения

25. Математическое описание процессов преобр.энергии в АД

Схема включения АД с фазным ротором и соответствующая ей схема двухфазной модели изображены на рисунках.

Математическое описание процессов эл.механического преобразования энергии в осях  и  можно получить из ранее приведенных уравнений положив в них U₂=0 и _к=0.

, где

Эти уравнения используются для анализа динамических свойств асинхронного ЭМП. В установившемся симметричном режиме работы двигателя переменные представляют собой сдвинутые относительно друг от друга по фазе синусоидальные величины, изменяющиеся в осях ,  с частотой сети: .

Представим эти переменные в виде вращающихся векторов U_1, I_1, U_1, I_1 и т.д. Т.к. переменные фазы  отстают от переменных фазы  на _эл=90, между ними очевидна связь: и .т.д. Учитывая это и имея ввиду, что производная по времени от вектора, неизменного по модулю и вращающегося со скоростью_0эл, может быть получена умножением этого вектора на j_0эл, т.е. например: , уравнения электрического равновесия для фазы статора и ротора можно представить в виде:

, т.к.

Для анализа статических режимов преобразования энергии выразим потокосцепления ₁ и ₂ через намагничивающий ток:

26. Естественные механическая и эл.Механическая характеристика ад.

Наиболее удобна для анализа работы АД Г-образная схема замещения с намагничивающим контуром, вынесенным на зажимы первичной сети. Здесь. Т.к.- мало, пренебрегаем им ,т.е. получаем.

Приняв для главной цепи поправочный коэффициент ₁, получим схему замещения, в которой: ;;;.

Используя известные из курса эл.машин выражения для электромагнитного момента:

и критического момента: .

И поделив одно на другое получим после преобразований

прямой линией, описываемой уравнением (в пределах до М_Н):.

Следует иметь в виду, что формулы Клосса, в т.ч. и упрощенная, достаточно точно описывают механические характеристики АД с фазным ротором. В к.з. АД, выпускаемых обычно с относительно глубокими пазами в роторе, либо с двойной клеткой ротора, имеется в той или иной степени явление вытеснения тока в стержнях ротора. Поэтому их параметры непостоянны и механические характеристики значительно отличаются от от характеристик, рассчитанных по формулам Клосса. Однако, эти формулы благодаря своей простоте позволяют выполнять многие расчеты и делать общие заключения о свойствах и работе АД. В тех же случаях, когда необходима большая точность, должны использоваться экспериментально снятые механические характеристики. У некоторых к.з. двигателей при малых скоростях механическая характеристика имеет провал,(см. рис.), вызванный влиянием высших гармоник поля, с чем следует считаться при пуске двигателя под нагрузкой.

Электромеханические характеристики АД представляют собой зависимости и. Т.к. ток ротора является основной величиной для оценки режима работы двигателя, рассмотрим графическую зависимость.

При использовании формул илиэто не всегда удается сделать в виду отсутствия данных о сопротивлениях обмоток двигателя.

В связи с этим для получения эл.механической характеристики воспользуемся формулой Клосса и выражением эл.магнитного момента.

, где , отсюда