4. Метод вузлових потенціалів

У даному методі за невідомі приймаються потенціали вузлів, після визначення яких можна знайти струм будь-якої гілки за законом Ома (для гілки з послідовним з'єднанням Е і R). Врахуємо, що завжди можна один з п вузлів кола заземлити і припустити, що його потенціал дорівнює нулеві. Отже, для визначення невідомих потенціалів потрібна система з рівнянь (виведення їх ілюструється на СРС-4).

В оста­точному вигляді вона формалізована аналогічно розглянутій у методі контурних струмів.

Використовувані позначення і , дістали назву вузлових струмів (потрібно відрізняти від контурних). Складові вузлових струмів і (струми джерел струму) записують із зна­ком "+", якщо і спрямовані до вузла, та із знаком "-" у протилеж­ному випадку. Опис методу доповнюємо такими примітками.

Примітка І. Якщо коло містить всього два вузли і (нехай вузол заземлено), то від системи залишиться лише одне рівняння: . Введімо позначення У результаті маємо:

(5)

Одержане співвідношення (5) називається розрахунковим рівнянням за методом двох вузлів (або методом вузлової напруги). За допомогою ві­домого далі розраховують струми гілок.

Примітка 2. Метод вузлових потенціалів тим вигідніший, чим мен­ше в колі вузлів. Тому тут нас цікавитимуть заходи, які дають змогу знизити кількість вузлів. До них належить, наприклад, перетворення ділянки з джерелом струму і паралельно під’єднаним до нього опо­ром на гілку з послідовним з'єднанням Е і R (причому ).

Доведення цього положення виконано далі. В основу його покладено еквівалентність струму , який виникав в навантаженні після під’єднання до затискачів зазначених ділянок опору .

Розглянутий захід корисний і в методі контурних струмів, оскіль­ки приводить до зменшення кількості незалежних контурів.

Алгоритм розрахунку параметрів кола за методом вузлових потенціалів

1. В схемі визначається кількість вузлів.

2. Один з вузлів обирається з нульовим потенціалом, заземлений.

3. Визначаються відомі та не відомі потенціали вузлів.

4. За кількістю невідомих потенціалів складається система рівнянь, яка містить:

ліворуч – суми добутку провідності (яка підходить до І-го вузлу) на потенціал цього вузлу, та добутків провідності з інших вузлів (до І-го вузлу) на відповідну між ними провідність, що береться з протилежним знаком;

праворуч – пишеться струм, що підходе до І-го вузлу через добуток джерел Е.Р.С. на провідності у відповідних гілках, або додаток джерел струму.

5. Підставлення чисельних даних в рівняння дає рішення будь яким засобом.

З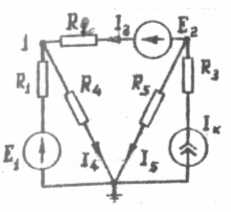 адано:

Треба скласти систему рівнянь для визначення та .

На підставі першого закону Кірхгофа:

Позначимо та назвемо

сума провідності гілок, які сходяться у першому вузлі;

провідність гілки, яка з’єднує перший та другий вузли;

вузловий струм першого вузла;

сума провідності гілок, які сходяться у другому вузлі;

провідність гілки, яка з’єднує другий та перший вузли;

вузловий струм другого вузлу.

В результаті одержуємо систему.

Примітка 3. В загальному випадку між першим та другим вузлами може бути кілько паралельних гілок. Тоді слід розглядати як суму провідності цих гілок, які взято з протилежним знаком «-».

Використовуючи встановлену логіку складання рівнянь, замінимо їх систему для кіл, які містять:

три вузли n-вузлів

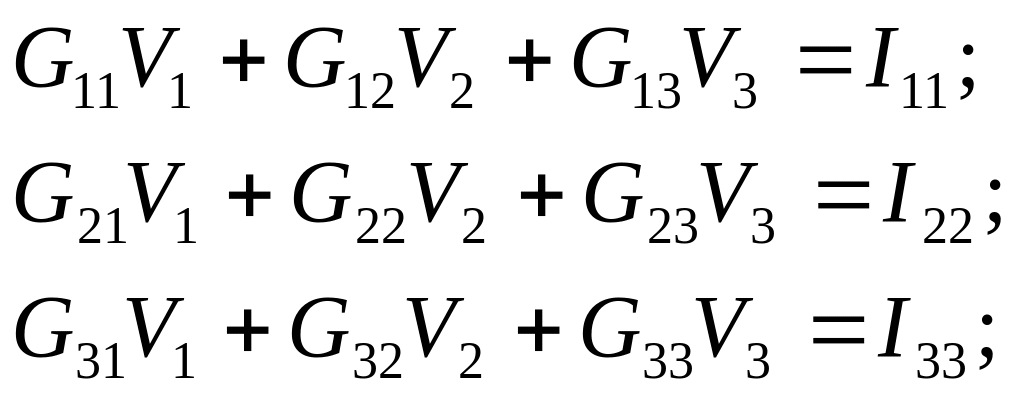
Далі, вирішуючи систему, знаходять потенціали вузлів, а потім визначають струми в гілках, що розшукують.

Алгоритм розрахунку:

• Для визначення невідомих потенціалів складаємо систему рівнянь;

• в середині схеми маркуємо напрям струмів за допомогою стрілок;

• в залежності від кількості невідомих потенціалів складаємо відповідну кількість рівнянь -1. Один з вузлів позначаємо як нульовий 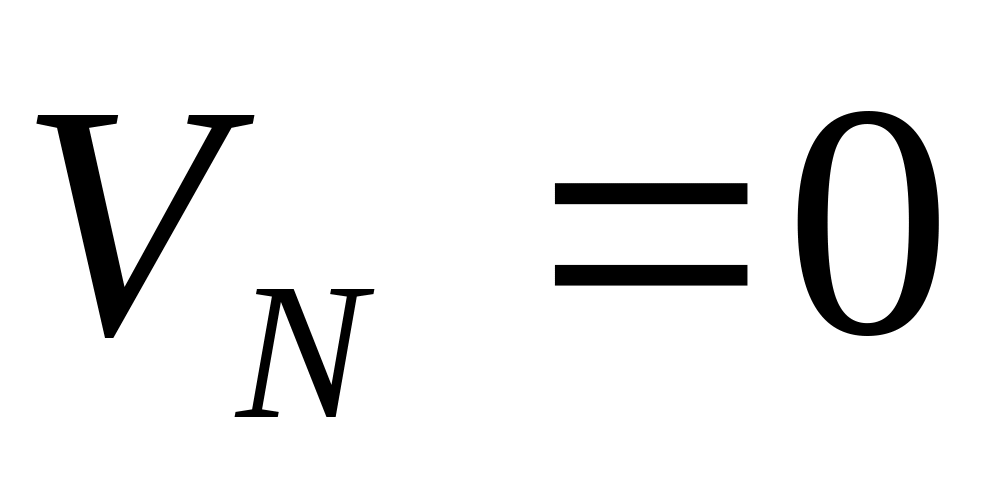(позначка елемента рівняння складає № вузла контуру до якого підходить елементи провідності. Якщо цифри однакові загальна сума провідності – позитивна, а якщо ні, сума провідності – негативна);

• Після складання системи рівнянь визначаємо провідності що підходять до вузлів та струми, що входять та виходять з вузла;

• Підставимо чисельні данні і вирішуємо систему відносно вузлових потенціалів.

• Знаючи потенціали розраховуємо в гілках схеми.