
- •3. Криволинейное движение
- •5. Закон сохранения импульса
- •[Править]Вывод из формализма Ньютона
- •[Править]Связь с однородностью пространства
- •[Править]Вывод из формализма Лагранжа
- •[Править]Закон сохранения импульса в общей теории относительности
- •9. Энергетические уровни
- •11. Потенциальная энергия заряда в электрическом поле
- •Вычисление циркуляции вектора в по замкнутому контуру
- •К теореме о циркуляции вектора в
- •13. Формула потока вектора противоречит принципу причинности
- •Может ли вектор течь?
- •Поток вектора напряженности или полная напряженность?
- •14. Проводник в электрическом поле
- •15. Электрическое поле в диэлектриках
1)
Материа́льная то́чка — простейшая физическая модель в механике — математическая абстракция — тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи.
Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.[1] Например, при расчёте пути, пройденного поездом, можно пренебречь его размерами, даже если путь измеряется сантиметрами.
При прямолинейном движении тела достаточно одной координатной оси для определения его положения.
Система отсчёта — это совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел[1].
Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f1(t), y = f2(t), z = f3(t).
В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п.
Ра́диус-ве́ктор (обычно
обозначается ![]() или
просто
или
просто ![]() )
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.
)
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.
Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.
Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.
Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называютвектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).
Можно
определить перемещение, как
изменение радиус-вектора точки: ![]() .
.
Модуль перемещения совпадает с пройденным путём в том и только в том случае, если при движении направление перемещения не изменяется. При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше.
Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго:
![]() .
.
Ско́рость (часто
обозначается ![]() ,
от англ. velocity или фр. vitesse) — векторная физическая величина,
характеризующая быстроту перемещения и
направление движения материальной
точки в
пространстве относительно выбранной системы
отсчёта (например, угловая
скорость).
Этим же словом может называться скалярная величина,
точнее модуль производной радиус-вектора.
,
от англ. velocity или фр. vitesse) — векторная физическая величина,
характеризующая быстроту перемещения и
направление движения материальной
точки в
пространстве относительно выбранной системы
отсчёта (например, угловая
скорость).
Этим же словом может называться скалярная величина,
точнее модуль производной радиус-вектора.
В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуетсяпроизводной функции.
Ускоре́ние (обычно
обозначается ![]() ,
в теоретической
механике
,
в теоретической
механике ![]() )
— производная скорости по
времени, векторная величина,
показывающая, насколько изменяется
вектор скорости точки
(тела) при её движении за единицу времени
(т.е. ускорение учитывает не только
изменение величины скорости, но и её
направления).
)
— производная скорости по
времени, векторная величина,
показывающая, насколько изменяется
вектор скорости точки
(тела) при её движении за единицу времени
(т.е. ускорение учитывает не только
изменение величины скорости, но и её
направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметриии равная 1 см/с2.
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
![]()
![]() .
.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
2. Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения.
УГЛОВАЯ СКОРОСТЬ
векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости , где - приращение угла поворота за промежуток времени ?t.
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно[1]:
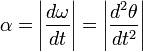
Вектор углового
ускорения α направлен
вдоль оси вращения (в сторону ![]() при
ускоренном вращении и противоположно
—
при замедленном).
при
ускоренном вращении и противоположно
—
при замедленном).
При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени[2], то есть
![]() ,
,
и направлен по касательной к годографу вектора в соответствующей его точке.
Существует связь между тангенциальным и угловым ускорениями:
aτ = αR,
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек2 .
Равномерное вращательное движение
Во
время равномерного вращательного
движения тело совершает движение по
окружности с одинаковой скоростью, но
с изменяющимся направлением. Например,
такое движение совершают стрелки часов
по циферблату.
Допустим, шар
равномерно вращается на нити длиной 1
метр. При этом он будет описывать
окружность с радиусом 1 метр. Длина такой
окружности: C
= 2πR = 6,28 м
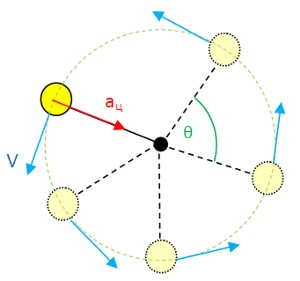 Время,
за которое шар полностью делает один
полный оборот по окружности,
называется периодом
вращения - T.
Чтобы
вычислить линейную скорость шара,
необходимо разделить перемещение на
время, т.е. длину окружности на период
вращения:
V
= C/T = 2πR/T
Период
вращения:
T
= 2πR/V
Если
наш шар будет делать один оборот за 1
секунду (период вращения = 1с), то его
линейная скорость:
V
= 6,28/1 = 6,28 м/с
Время,
за которое шар полностью делает один
полный оборот по окружности,
называется периодом
вращения - T.
Чтобы
вычислить линейную скорость шара,
необходимо разделить перемещение на
время, т.е. длину окружности на период
вращения:
V
= C/T = 2πR/T
Период
вращения:
T
= 2πR/V
Если
наш шар будет делать один оборот за 1
секунду (период вращения = 1с), то его
линейная скорость:
V
= 6,28/1 = 6,28 м/с
3. Криволинейное движение
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на осиOx и Oy и координаты x и y точки в любой момент времени t определяется по формулам
![]()
![]()
![]()
![]()
![]()
Частным
случаем криволинейного движения –
является движение по окружности. Движение
по окружности, даже равномерное, всегда
есть движение ускоренное: модуль скорости
все время направлен по касательной к
траектории, постоянно меняет направление,
поэтому движение по окружности всегда
происходит с центростремительным
ускорением ![]() где r –
радиус окружности.
где r –
радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
При
криволинейном движении ускорение можно
представить как сумму нормальной ![]() и
тангенциальной
и
тангенциальной ![]() составляющих:
составляющих:
![]() ,
,
- нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:
![]()
v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.
- тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.
Полное ускорение, с которым движется материальная точка, равно:
![]() .
.
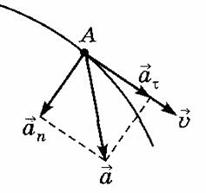
Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.
Период обращения— это время, за которое тело совершается один оборот.
Обозначается период буквой Т (с) и определяется по формуле:
![]()
где t — время обращения, п — число оборотов, совершенных за это время.
Частота обращения— это величина, численно равная числу оборотов, совершенных за единицу времени.
Обозначается
частота греческой буквой ![]() (ню)
и находится по формуле:
(ню)
и находится по формуле:
![]()
Измеряется частота в 1/с.
Период и частота — величины взаимно обратные:
![]()
Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив скорость v на время одного оборота:
l = vT. С другой стороны, этот путь равен длине окружности 2πr. Поэтому
vT = 2πr,
![]()
![]()
где w (с-1) - угловая скорость.
При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.
Угловая скорость (w) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:
![]() .
.
Связь между линейной и угловой скоростями:
v= wr.
Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.
4.
Динамика материальной точки и поступательного движения твердого тела |
|
Справочные сведения |
Основной
закон динамики (второй закон Ньютона)
материальной точки
имеет вид
В
случае
Центр
масс системы материальных точек
определяется по формуле
Скорость
центра масс системы
Уравнение
движения тела переменной массы
(уравнение Мещерского)
Закон
Гука Сила
трения скольжения |
Примеры решения задач |
При решении задач по динамике материальной точки необходимо прежде всего выяснить, какие силы действуют на тела рассматриваемой механической системы и изобразить их на рисунке. Затем нужно выбрать систему отсчета, относительно которой рассматривается движение. Координатные оси системы целесообразно располагать так, чтобы проекции сил на эти оси определялись наиболее просто. Для каждого тела системы необходимо записать второй закон Ньютона в векторной форме и спроектировать его на оси выбранной системы координат. Иногда оказывается, что полученных динамических уравнений недостаточно для решения задачи (в случае движения системы тел). Тогда необходимо дополнить систему уравнений кинематическими условиями, обусловленными связями, существующими между телами. Рассмотрим конкретные примеры. Задача
1. Частица
массы
со
скоростью |
Решение |
Будем рассматривать движение частицы в проекциях на направление действия тормозящей силы и перпендикулярное к нему (рис. 1.2.1).
Рис. 1.2.1 В первом случае движение будет равнозамедленным, и его кинематические уравнения можно записать в виде
Движение
в перпендикулярном к вектору силы
направлении будет равномерным с
постоянной скоростью
По условию через некоторое время вектор скорости образует с вектором силы угол β, откуда следует
Из (1.2.2) находим время движения частицы в области действия тормозящей силы
Согласно
второму закону Ньютона
Подставляя (1.2.3) в (1.2.1), после несложных преобразований находим ширину области действия тормозящей силы
Предельно
возможная ширина области действия
силы может быть получена из (1.2.4), если
положить
Задача
2.
Каковы должны быть модуль и направление
минимальной силы
,
приложенной к бруску, лежащему на
горизонтальном столе, чтобы сдвинуть
его с места? Масса бруска |

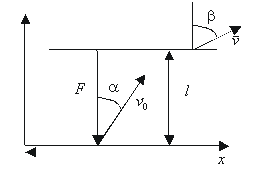
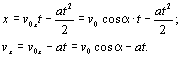 , (1.2.1)
, (1.2.1)