Теоретические задания для развития и контроля владения компетенциями
1.
Дайте определение первообразной функции
для данной функции
на данном промежутке.
2. Как связаны между собой две первообразные для функции в некотором промежутке?
3. Что называется неопределенным интегралом от функции ?
4. Сформулируйте основные свойства определенного интеграла (правила интегрирования).
5. Составьте таблицу основных интегралов.
6. В чем суть метода непосредственного интегрирования?
7. Сформулируйте теорему об инвариантности формул интегрирования.
8. Запишите формулу замены переменной в неопределенном интеграле.
9. Когда целесообразно применять замену переменной интегрирования?
10. Запишите формулу интегрирования по частям.
11. Когда целесообразно применение способа интегрирования по частям?
12. Интегралы какого вида можно вычислять с помощью формулы интегрирования по частям?
13.
Что принимается за
для интегралов вида
(
- многочлен)?
14.
Что принимается за
для интегралов вида
(
-многочлен)?
Примеры решения типовых задач
1. Проверьте справедливость формулы
Решение. Справедливость формулы проверим дифференцированием. Убедимся в том, что производная от правой части формулы равна подынтегральной функции. В самом деле,
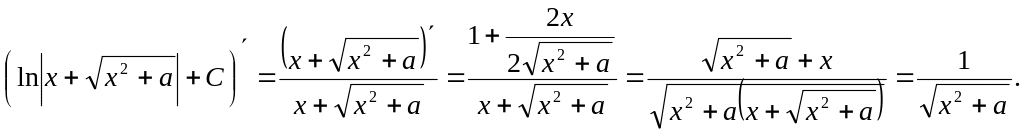
Таким образом, справедливость формулы доказана.
2. Вычислите неопределенные интегралы
1)
Решение. Разлагаем подынтегральную функцию на слагаемые, деля числитель почленно на знаменатель. Затем интегрируем каждое слагаемое отдельно, вынося постоянные множители за знаки интегралов:
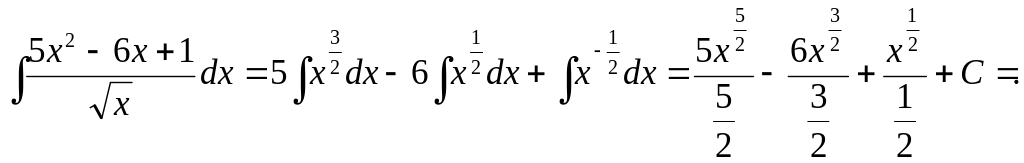
2)
.
Решение.
Так
как
,
то преобразуя дифференциал и применяя
теорему об инвариантности формул
интегрирования, получим
3)
Решение.
Этот интеграл вычисляется методом
замены переменной. Положим
тогда
Отсюда имеем
Возвращаясь к старой переменной, окончательно получим
4)
Решение. Этот интеграл берется по частям. В качестве берем многочлен:
Замечание.
Интегралы
вида
,
- многочлен, берутся по частям. В качестве
берем многочлен и интегрируем по частям
столько раз, какова степень многочлена.
5)
Решение. Этот интеграл берется по частям:
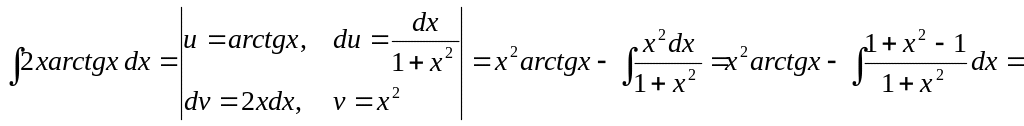
Замечание.
Интегралы вида
,
где
- многочлен, берутся по частям. В качестве
берем функции
6)
Решение.
Интегралы
вида
берутся
по частям последовательно два раза,
причем за
оба раза выбирается либо показательная
функция, либо тригонометрическая. После
двукратного интегрирования получается
линейное уравнение относительно искомого
интеграла.
Следуя этому правилу, получим:
Таким образом, имеем уравнение:
или
Откуда
7)
Решение. Этот интеграл относится к классу интегралов, берущихся по частям:
.
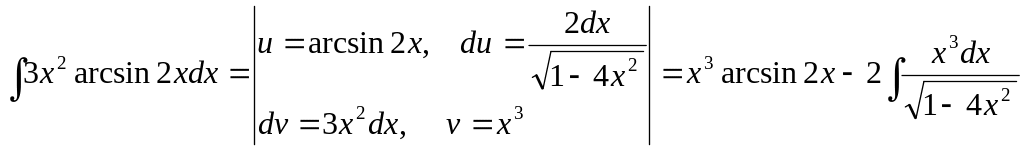Для
вычисления интеграла
используем метод замены переменной
интегрирования:
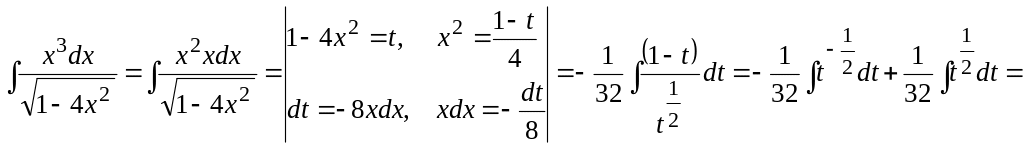
Окончательно
имеем:
.
Замечание. При вычислении многих интегралов приходится применять несколько методов интегрирования, как, например, в последнем примере.
Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
1.
Даны пары функций. Из каждой пары выпишите
ту функцию, которая является первообразной
для другой, и обозначьте ее через
а)
и
б)
и
в)
и
г)
и
д)
и
е)
и
2.
Найдите первообразные следующих функций
и результаты проверьте дифференцированием:
а)
б)
в)
г)
д)
е)
3. Вычислите методом непосредственного интегрирования:
а)
б)
в)
;
г)
д)
;
е)
.
4. Преобразуя дифференциал, сведите интегралы к табличным и вычислите их:
а)
;
б)
;
в)
;
г)
;
д)
.
5. Методом замены переменной вычислите интегралы:
а)
;
б)
;
в)
.
6. Вычислите интегралы методом интегрирования по частям:
а)
;
б)
;
в)
;
г)
;
д)
.
7. Вычислите интегралы:
а)
;
б)
;
в)
.