8. Понятие функции. Способы задания функции.

Пусть X и каждому элементу из мно-ва Х по некоторому закону сопоставлено действительное число f(x)

Значит задана числовая функция y=f(x).

Графиком функции y=f(x) называется мно-во точек на плоскости вида (x, f(x)), где х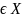 , где Х – Область определения функции.

Способы задания:

Формула (аналитический).

Табличный.

Графический способ.

8. Предел функции. Эквивалентность определений пределов функции. Примеры.

Число b называется пределом функции f(x) в точке x=a (или при x стремящемся к а), если ∀{х_n} сходящейся к числу а ; ее элементы х_n ≠ а соответствующая последовательность {f(x_n)} сходится к b. ( по гейне)

Пусть f(x) определена в некоторой окрестности точки a, за исключением быть может самой точки а. Число b называется пределом функции f(x) в точке х=а (х→а)Если ∀ε > 0 ∃ δ= δ(ε)>0 ; ∀х 0<|x-a|< δ : |f(x) – b| < ε

Т: Определения эквивалентны.

Примеры: lim 2x = a; функция дерифле.

8. Свойства пределов функций, связаные с арифметическими операциями и переходом в неавенства.

Т: Пусть lim f(x) = A, lim g(x) = B, тогда их сумма\разность\произведение\деление\ равна …

T: Пусть lim f(x) = A, lim g(x) = B и ∃ U(a) ; ∀x ϵ U(a), x ≠ а : f(x) ≤ g(x), тогда A ≤ B.

Т: lim f1(x) = b, lim f2(x) = b и ∃ U(a) ; ∀x ϵ U(a), x ≠ а : f1(x) ≤ g(x) ≤ f2(x), тогда lim g(x) = b.

8. Локальная ограниченность. Критерий Коши о существовании предела.

Т: Пусть lim f(x) = b, b – конечное число, тогда ∃ U(a) и М>0 ; ∀x ϵ U(a), x ≠ а : |f(x)|≤ M.

Т: Для того, чтобы ∃ lim f(x) необходимо и достаточно, чтобы функция f(x) была определена на некоторой окрестности точки а, кроме быть может самой точки а, и для ∀ε > 0 ∃ U(a) ; ∀ x^’ x^” ϵ U(a) x^’≠a, x^”≠a : f(x^’ ) – f (x^”) < ε

8. Теорема о сохранении знака функции, имеющей предел.

Т: lim f(x) = b, где b конечное число и b≠0, тогда ∃ U(a) ; ∀x ϵ U(a), x ≠ а : |f(x)|>

26) Бм и бб функции. Связь функций имеющих предел.

Функция α(х) называется бмф, если lim α(х) = 0.

Л: Конечный предел lim f(x) = b существует титтк функцию f(x) можно представить в виде f(x) = b + α(х)

Т: для бмф справедливы свойства, что и для бмп.

Т: ∑ и ∏ конечного числа бесконечно малых при х →а функций, а также ∏ бмф на ограниченную, так в в же является бмф при х →а.

Функция f(x) называется ббф, если ∀M>0 ∃ U(a) ; ∀x ϵ U(a), x ≠ а : |f(x)|>M.

If f(x) – бмф, то 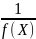– ббф.

If f(x) – ббф, то – бмф.

8. Односторонний предел. Критерий существования предела в терминах одностор пределов

Число С называется пределом функции f(X) справа(слева) if ∀ {х_n} ; х_n>a (х_n<a) : lim f(х_n) = C.

Конечное число С называется lim f(x) = a справа(слева) Если ∀ε > 0 ∃ δ= δ(ε)>0 ; ∀x ; a<x<a+ δ (a- δ<x<a)

: |f(x) – c | < ε.

Т:у f(x) ∃ предел в точке х = а титтк в этой точке ∃ предел справа и предел слева, притом они равны f(a-0)=f(a+0)=c, тогда lim f(x) = c.

28) Непрерывность функции в точке. Примеры непрерывности.

f(x) называется непрерывной в точке x₀ , если она определена в некоторой окрестности точки x₀ в том числе и в самой x₀ , Тогда справедливо : lim f(x) = f(x₀)

f(x) называется непрерывной в точке x₀ , если она определена в некоторой окрестности точки x₀ в том числе и в самой x₀ , Тогда справедливо :

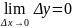
Эквивалентность определений.

Примеры: y=c y=x y=sinx

29) Свойства непрерывных функций. Сохранение знака. Локальная ограниченность.

Т: Если f(X) и g (x) непрерывны в точке a , то их сумма\разность\произведение\частное тоже непрерывны в этой точке

Т: Если f(X) непрерывна в точке а и ∃ окрестность в точке а и ∃ M>0 ; ∀x ϵ U(a) : |f(x)| < M.

Т: Если f(X) непрерывна в точке а и f(a) ≠0, то ∃ U(a) ; ∀x ϵ U(a) : |f(x)| > .

30) Непрерывность сложной функции.

Пусть ϕ(х) отображает мно-во Х в мно-во У, соответственно z=f(y) отображает УZ, тогда говорят

Z=f(ϕ(х)) называется сложной функцией ХZ

Z= F1(F2(….)) суперпозиция функций.

Т: Пусть y=ϕ(х) непрерывна в т х=а, а функция z=f(y) непрерывна в т y=b, тогда z=f (ϕ(х))=F(x) непрерывна в т х=а.

31) Первый замечательный предел.

32) Второй замечательный предел.

33) Теорема Коши о нуле непрерывной функции.

Т: Пусть f(x) непрерывна на отрезке [a,b] и числа f(a), f(b)≠0 и имеют разные знаки, тогда ∃, по крайней мере, одна тоска С ϵ (a,b), в которой f(c)=0.

C: : Пусть f(x) непрерывна на отрезке [a,b], f(a) = A, f(b) = B и пусть A≠B, пусть С – произвольное число, расположенное между А и В. Тогда ∃, по крайней мере, одна тоска С ϵ (a,b), в которой f(c)=С.

34) Непрерывность обратной функции.

Т: Пусть f(x) строго возрастает на [a,b] и непрерывная на этом отрезке и пусть α=f(a) β=f(b), тогда

1. образом отрезка [a,b] при отображении y=f(x) является отрезок [ α, β ]

2. ∃ обратная функция x=g(y) строго возрастающая однозначная и непрерывная на отрезке [ α, β ]

Л: Пусть f(x) строго возрастает на [a,b] и отображает этот отрезок на [ α, β ], тогда функция y=f(x) непрерывна на отрезке [a,b]

35) Непрерывность элементарных функций.

Т: Всякая основная элементарная функция непрерывна на области определения.

36)Сравнение порядков бесконечно малых функций.

Бмф α(x) называется бмф более высокого порядка, чем бмф β(x) при xa , если 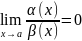, значит β(x) более низкого порядка.

Бмф при xa α(x) и β(x) называются бм одного порядка при xa Если ∃ U(a) такая окрестность в точки а , а так же ∃ M>0, m>0 ; ∀x ϵ U(a) , x=a : m ≤ 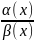≤M. То есть одну бм, можно оценить через другую. В частности ∃ 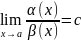, где с- конечное число и с≠0, то эти бм имеют один и тот же порядок.

37) Эквивалентные функции. Вычисление пределов при помощи эквивалентных функций.

Функции α(x) и β(x) называются эквивалентными при xa , если .

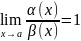Т: Пусть α(x) ∼ α₁(x) β(x) ∼ β₁(x) при xa тогда, Если ∃ , то ∃ :

=

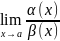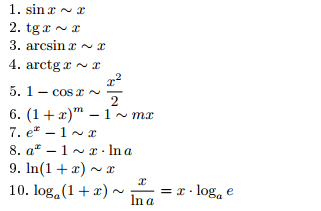
38)Символы Ландау. Критерий эквивалентности функций.

39)Классификация разрывов. Примеры.

40) Первая теорема Вейерштрасса.

41) Вторая теорема Вейерштрасса.

42) Равномерная непрерывность. Примеры.

43) Теорема Кантора.