1. Множества и операции над множествами.

Множество – совокупность объектов произвольной природы. Объекты, входящие в состав множества -элементы этого множества.

Подмножество -

Объединение или сумма -

Пересечение или произведение -

Разность -

2. Действительные числа. Числовые множества.

Что это такое

Операции

Интервалы\отрезки

3. Свойства действительных чисел. ∀ε > 0

+ (4)

* (4)

*+

Упорядоченность

Беспрерывность

Тривиальность

4. Ограниченные и неограниченные множества.

Множество Х – ограничено сверху  ∃ М ϵ R ; ∀ хϵХ : х≤ М / снизу…

Множество Х наз ограниченным (2 варианта).

Лемма об эквивалентности определений.

Множество Х наз неограниченным –

Максимальное и минимальное число во множестве.

Т : если максимум существует, то он единственный и ограничивает сверху Х.

5. Точные верхние и нижние грани числовых множеств. Теорема о существовании точной грани.

Если мно-во ограничено сверху, то оно имеет бесконечное число верхних граней.

Sup(x) and inf (x)

Число М называют точной верхней гранью, если оно удовлетворяет:

1. ∀ хϵХ : х≤М

2. ∀ε > 0 ∃ хϵХ : x> M- ε

T: Всякое ограниченное сверху( не пустое) множество Х ϵ R имеет точную верхнюю грань.

6. Числовые последовательности. Ограниченные и неограниченные последовательности.

Пусть каждому натуральному числу по некоторому закону сопоставлено действительное число х_n , тогда говорят, что задана числовая последовательность.

Числовые операции.

Определение ограниченности (2) ∃ M,m ; ∀ nϵN : m≤ х_n≤M ∃ A ; ∀ nϵN : |х_n| ≤A

Доказательство эквивалентности определений.

Неограниченные

7. Бесконечно малые и бесконечно большие последовательности. Отношения между бесконечно большими и неограниченными последовательностями.

{α_n} – бмп, if ∀ε > 0 ∃ N=N(ε) ; ∀n > N(ε) : | α_n| < ε

{β_n} – ббп, if ∀A > 0 ∃ N=N(A) ; ∀n > N(A) : | β_n| > A

Любая ббп является неограниченной (видно из определения) !Обратное утверждение неверно. {010203..}

8. Свойства бесконечно малых последовательностей. Связь бесконечно малых и бесконечно больших последовательностей.

Сумма/разность бмп = бмп. ( по определению бмп и ε=0.5) + (неравенство треугольника)

Если все элементы ббп отличны от 0, то 1/ббп = бмп

Если все элементы бмп отличны от 0, то 1/бмп = ббп

Л: Произведение бмп на ограниченную = бмп (ε/A по определению)

Следствие из Л: с*бмп = бмп, где с - константа

8. Теорема о промежуточной бесконечно малой последовательности.

Т: Пусть {α_n} и {β_n} – бмп и {γ} – промежуточная, тогда ∀nϵN : α_n ≤ γ_n ≤ β_n

8. Предел числовой последовательности. Единственность предела. Ограниченность сходящейся последовательности.

Число а называют пределом последовательности {х_n}, если {х_n - а} – бмп.

Число А называют пределом последовательности {х_n}, если ∀ε > 0 ∃ N=N(ε) ; ∀n > N(ε) : | х_n - А| < ε

Число А называют пределом последовательности {х_n}, если в любой ε окрестности точки А находятся все элементы этой последовательности, начиная с какого-то номера.

Если числовая последовательность имеет предел, то она называется сходящейся.

Т: Сходящаяся посл. может иметь только один предел (от противного)

Т: Сходящаяся посл. ограничена (через определение и неравенство треуг) (обратное – неверно) {(-1)ⁿn}

8. Свойства пределов связанные, с арифметическими операциями над последовательностями.

Т: Если {х_n} и {y_n} сходящиеся, то их +-/* тоже сходящиеся. (по определению предела и свойства бмп)

Л: Если , то { } – ограниченная.

8. Свойства пределов последовательностей, связанные с переходом к пределу в неравенствах.

Т: Пусть 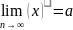и ∀nϵN : x_n ≤ y_n Тогда а ≤ b. (от противного)

Т: Если все элементы сходящейся последовательности {х_n} принадлежат отрезку [a,b], то и предел

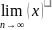будет также принадлежать этому отрезку.

Т: Пусть ∀nϵN х_n ≤ у_n ≤ z_n и пусть ∃ 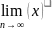= тогда .

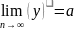8. Монотонные последовательности. Признак сходимости монотонной последовательности.

{х_n} называется неубывающей, если ∀nϵN : х_n+1 ≥ x_n . Ограничена снизу своим первым элеметом.

Т: Если неубывающая последовательность ограничена сверху, то она сходящаяся.

Док-во: ( Через точную верхнюю грань и определение монотонности)

8. Число е.

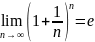(через Бином Ньютона доказываем, что возрастает, и что ограничена сверху)

8. Принцип вложенных отрезков.

Пусть дана бесконечная система отрезков δ_n=[a_n,b_n] nϵN вложенных друг в друга, то есть δ_n+1 > δ_n

C ∀nϵN, с длинами стремящимися к нулю. 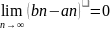. Тогда ∃ и при том единственная точка С, принадлежащая всем отрезкам. (по признаку сходимости монотонной последовательности, а потом единственность от противного)

8. Подпоследовательности. Частичные пределы. Теорема Больцана-Вейерштрасса.

Пусть последовательность, выведем из нее бесконечное число с номерами (1<2<3….). В результате получаем новую последовательность, которая называется подпоследовательностью.

Пределы подпоследовательностей – частичные пределы.

Л: Пусть {х_n} сходится и имеет предел =а. Тогда любая ее подпоследовательность сходится также сходится и имеет предел = а. (Определение сходимости и опр. подпоследовательности)

Утв: Всякая сходящаяся последовательность ограничена, обратное утв неверно

Т Б-В: Из любой ограниченной последовательности можно выделить сходящуюся подпос-сть

(Разбиваем на отрезки, тС – единственная, кот принадлежит всем, значит все сходится к ней)

Л: Для любой неограниченной последовательности можно выделить ббп (по опр ббп)

8. Критерий сходимости в последовательностях в терминах частичных пределов.

Т: Для того, чтобы ограниченная последовательность являлась сходящейся необходимо и достаточно, чтобы она имела единственный частичный предел.

(необходимаость – если сходится, значит имеет частичный предел.)

(достаточность – от противного берем обратное определение предела)

8. Верхний и нижний предел последовательности. Существование верхнего предела у ограниченной последовательности.

Верхний предел огр сверху последовательности, называется наибольший из частичных пределов данной п-сти)

Т: M=sup L и m = inf L являются частичными пределами ограниченной посл-ти {х_n}. (через жопу)

Л: Ограниченная посл-ть сходится титт, когда ее верхний и нижний предел совпадают.

8. Характеристика верхнего предела на языке n – ε

Для того, чтобы число М являлось верхним пределом ограниченной {х_n} необходимо и достаточно, чтобы она удовлетворяла следующим условиям:

1. ∀ε > 0 ∃ N=N(ε) ; ∀n > N(ε) : х_n < ε + М (Правее М находится конечное число элементов)

2. ∀ε > 0 ∃ N; n₀>N : M – ε < x₀ (Сущ элементы с огромными номерами, лежащие близко к М)

8. Критерий Коши сходимости последовательностей.

{х_n} называется фундаментальной, если ∀ε > 0 ∃ N=N(ε) ; ∀n,m > N(ε) : | x_n-x_m| < ε

{х_n} называется фундаментальной, если ∀ε > 0 ∃ N=N(ε) ; ∀n > N(ε) и∀ Р≥0 : | x_n+р-x_n| < ε

Т: Для того, чтобы {х_n} являлась сходящейся необходимо и достаточно, чтобы она была фунд-ной.

( сход -> фунд: опр предела + опр фунд и ε/2)

( фунд->сход: 1) раз ограничена, значит по Б-В из нее можно выделить сход п-псть част предел)

2)Что {х_n} сходится к этому частичному пределу.