
- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
Глава 4. Линии передачи электромагнитной энергии
Направляемые электромагнитные волны
В практике важное значение имеет решение задачи по передаче электромагнитной энергии от генератора к потребителю. Выполнить такую передачу электромагнитной энергии можно с помощью линии передачи.
Линия передачи – это устройство, предназначенное для передачи энергии от генератора к потребителю.
На высоких частотах и на большие расстояния электромагнитная энергия передается с помощью излучающих систем (антенн). В этом случае энергия распространяется в свободном пространстве, т.е. в окружающей среде.
На высоких частотах и на малые расстояния, а также на низких частотах передачу электромагнитной энергии осуществляют с помощью направляющих систем. В основе направляющей системы лежит способность металлической поверхности направлять движение электромагнитной волны. Также для этой цели используется граница раздела двух диэлектриков.
Передать электромагнитную энергию можно с помощью двухпроводной, ленточной, коаксиальной, микрополосковой линии, волноводов разных типов, а также некоторых других линий передачи. На рис. 4.1. показаны некоторые линии передачи электромагнитной энергии, получившие широкое распространение.

Рис. 4.1
Виды линий передач электромагнитной энергии: а) двухпроводная линия; б) полосковая линия, разделенная диэлектрической прокладкой; в) однопроводная линия в виде круглого провода; г) однопроводная линия в виде провода с диэлектрическим покрытием; д) диэлектрическая линия; е)коаксиальный круглый волновод; ж)прямоугольный волновод; з) круглый волновод; и) П-образный волновод; к) Н-образный волновод; л) эллиптический волновод.
Металлические волноводы применяются в СВЧ-диапазоне, включаюем волны 1100 мм. Иногда в этом диапазоне применяют диэлектрические волноводы. В оптическом диапазоне применяют диэлектрические (стеклянные) волноводы – нити, которые назвали световодами.
Металлический волновод имеет две пары параллельных металлических поверхностей, т.е. представляет собой трубу прямоугольного сечения, внутри которой распространяется электромагнитная волна.
Распространение электромагнитной волны в волноводе прямоугольного сечения начнем рассматривать с направляющей системы, состоящей из одной металлической плоскости.
Падение плоской электромагнитной волны с вертикальной поляризацией поля на идеально проводящую плоскость
Пусть из вакуума на идеально проводящую плоскость под углом падает плоская монохроматическая волна, имеющая вертикальную поляризацию (рис. 4.2).
На рис. 4.2 показаны
мгновенные положения последовательности
волновых фронтов, отстающих друг от
друга на расстояние![]() .
Поэтому фазы поля для соседних положений
фронтов отличаются на величину 180.
На рис. 4.2 также показаны взаимные
ориентации векторов для падающего
фронта волн
.
Поэтому фазы поля для соседних положений
фронтов отличаются на величину 180.
На рис. 4.2 также показаны взаимные
ориентации векторов для падающего
фронта волн
![]() ,
,![]() .
.
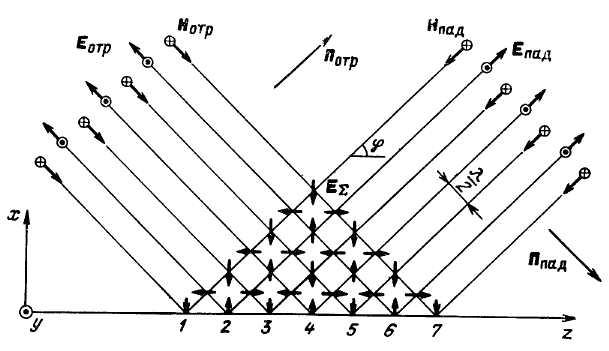
На границе идеального
проводника выполняются граничные
условия, т.е.
![]() .
В нашем случае это условие будет
выполняться, если будет существовать
отраженная волна. На рис. 4.2 показаны
поверхности равных фаз для отраженной
волны, причем векторы электромагнитного
поля отраженной волны, обозначенные
.
В нашем случае это условие будет
выполняться, если будет существовать
отраженная волна. На рис. 4.2 показаны
поверхности равных фаз для отраженной
волны, причем векторы электромагнитного
поля отраженной волны, обозначенные![]() ,
,![]() ,
обладают свойствами:
,
обладают свойствами:
модуль коэффициента отражения равен 1, поэтому амплитуды падающей и отраженной волны одинаковы по величине, т.е.
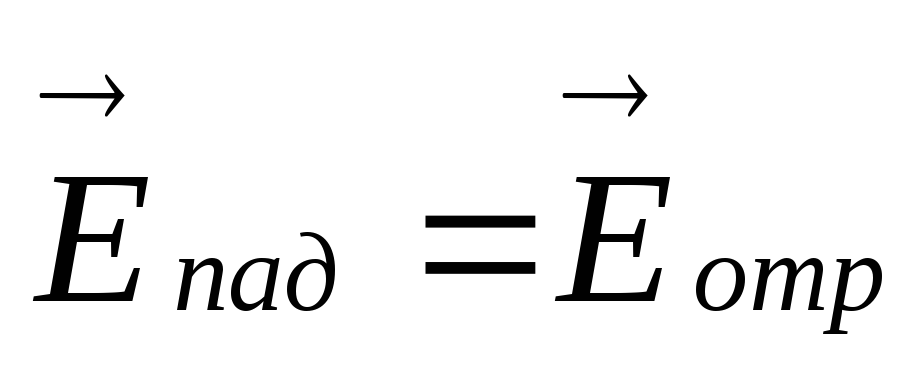 ,
,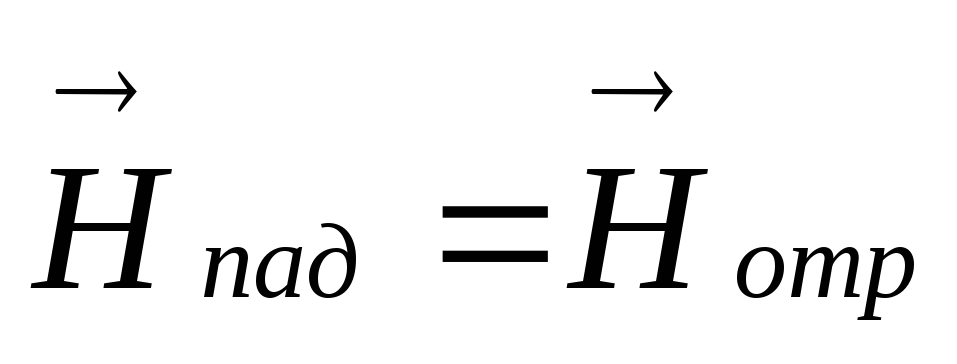 .
.на границе раздела выполняются граничные условия, т.е.
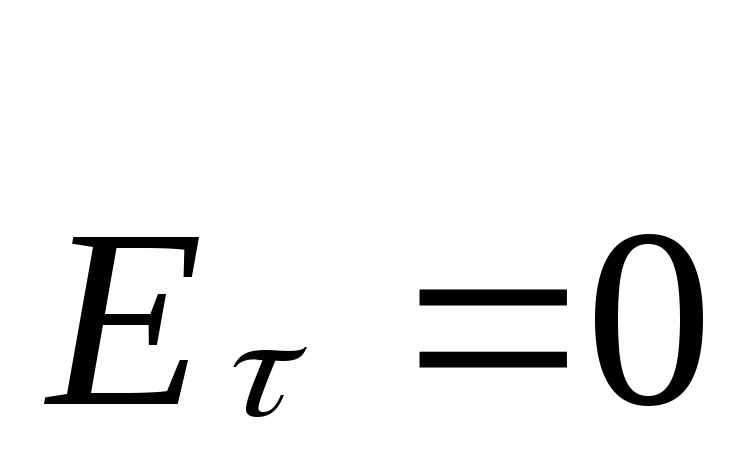 ,
или
,
или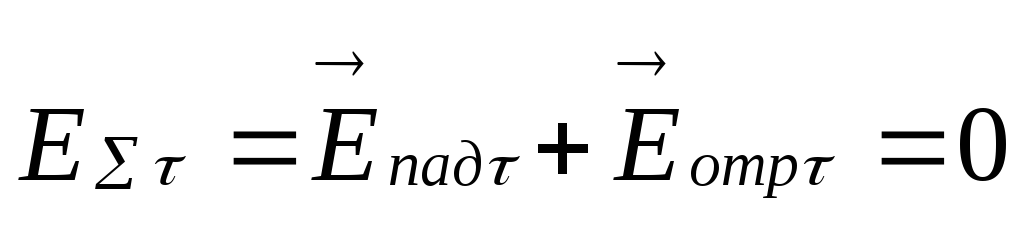 ,
где
,
где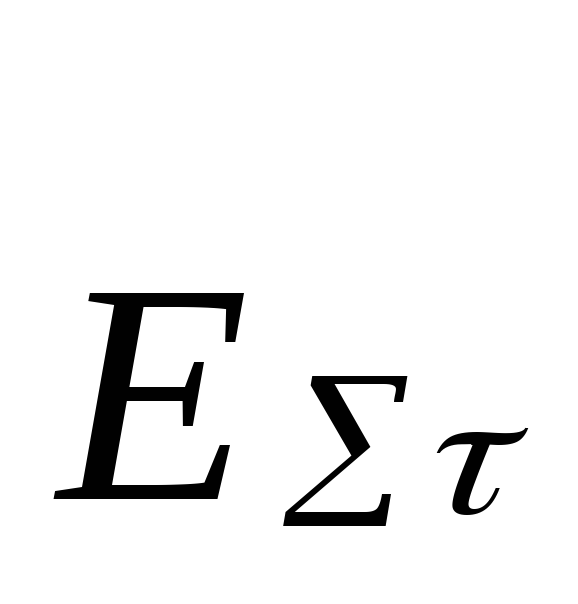 - суммарные тангенциальные составляющие,
- суммарные тангенциальные составляющие,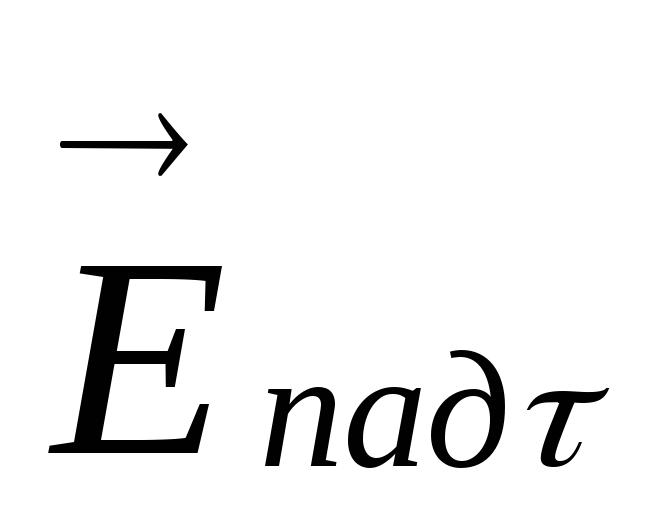 - тангенциальные составляющие падающей
волны,
- тангенциальные составляющие падающей
волны,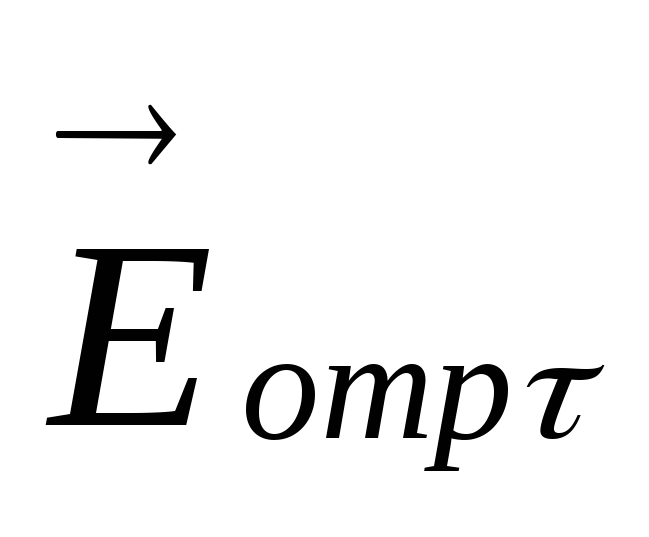 - тангенциальные составляющие отраженной
волны.
- тангенциальные составляющие отраженной
волны.
На рис. 4.2 показан результат сложения полей падающей и отраженной волны. Результат сложения сделан в узлах образующейся сетки волновых поверхностей. Из результатов сложения волновых процессов следуют следующие выводы:
Суммарные силовые линии магнитного поля имеют вид бесконечных нитей, направленных параллельно оси OY;
Векторы напряженности электрического поля лежат в плоскости XOZ, причем ориентация этих векторов непрерывно меняется от точки к точке.
Из рис. 4.2 видно, что силовые линии напряженности суммарного поля имеют определенную закономерность в пространстве. Подчеркнем, в сложении участвовали волновые фронты, положение которых отличалось по фазе на (противофаза). Если привести более детальное сложение и изобразить результирующее суммарное поле для электромагнитной волны с вертикальной поляризацией, то получим картину силовых линий, показанную на рис. 4.3.
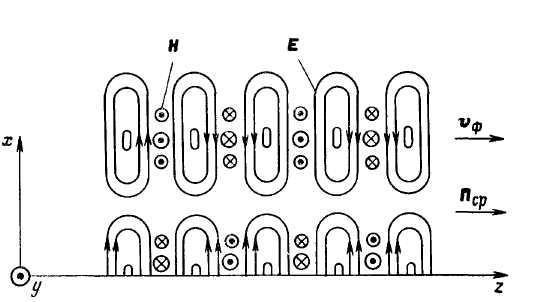
Из рис. 4.3 видно,
что силовые линии напряженности поля
![]() перпендикулярны металлической
поверхности. Также видно, что в замкнутых
линиях
перпендикулярны металлической
поверхности. Также видно, что в замкнутых
линиях![]() можно выделить участки, которые
перпендикулярны направлению распространенияz.
Также имеются участки, которые совпадают
с направлением распространения. Такая
результирующая волна называется волной
Е-типа, т.к. имеются составляющие, которые
и перпендикулярны, и продольны направлению
распространению волны вдоль оси z.
можно выделить участки, которые
перпендикулярны направлению распространенияz.
Также имеются участки, которые совпадают
с направлением распространения. Такая
результирующая волна называется волной
Е-типа, т.к. имеются составляющие, которые
и перпендикулярны, и продольны направлению
распространению волны вдоль оси z.
Магнитное поле
![]() имеет только составляющие, перпендикулярные,
т.е являются поперечными, направлению
распространения волны. Поэтому волны
Е-типа называются также ТМ-волнами, т.е.
поперечными магнитными волнами.
имеет только составляющие, перпендикулярные,
т.е являются поперечными, направлению
распространения волны. Поэтому волны
Е-типа называются также ТМ-волнами, т.е.
поперечными магнитными волнами.
Аналогичным образом
можно рассмотреть падение плоской
электромагнитной волны с горизонтальной
поляризацией из воздуха на плоскую
проводящую поверхность. Не останавливаясь
на рассмотрении такого падения
электромагнитной волны детально, покажем
результирующее поле с помощью силовой
картины, содержащей и суммарный вектор
![]() ,
и суммарный вектор
,
и суммарный вектор![]() (рис. 4.4).
(рис. 4.4).

Рис. 4.4
Волна также
распространяется вдоль оси z.
Напряженность магнитного поля
![]() изменяется в плоскостиXOZ.
Вектор напряженности электрического
поля колеблется вдоль оси y.
изменяется в плоскостиXOZ.
Вектор напряженности электрического
поля колеблется вдоль оси y.
Из рис. 4.4 видно,
что силовые линии
![]() замкнуты, причем на таких замкнутых
линиях можно выделить участки, которые
являются параллельными (продольными
составляющими) оси распространения.
Также в замкнутых линиях
замкнуты, причем на таких замкнутых
линиях можно выделить участки, которые
являются параллельными (продольными
составляющими) оси распространения.
Также в замкнутых линиях![]() можно выделить участки, перпендикулярные
(поперечные) направлению распространения.
Таким образом, в результирующей волне
содержатся одновременно и поперечные,
и продольные составляющие. Такая
электромагнитная волна называется
волной Н-типа. Подчеркнем, что волна
Н-типа содержит одновременно две
составляющие. Любой другой участок
замкнутой линии можно представить
суммой поперечной и продольной
составляющих поля.
можно выделить участки, перпендикулярные
(поперечные) направлению распространения.
Таким образом, в результирующей волне
содержатся одновременно и поперечные,
и продольные составляющие. Такая
электромагнитная волна называется
волной Н-типа. Подчеркнем, что волна
Н-типа содержит одновременно две
составляющие. Любой другой участок
замкнутой линии можно представить
суммой поперечной и продольной
составляющих поля.
Волна Н-типа имеет
и другое название: ТЕ, т.е поперечно
электрическая волна. Действительно, в
волне Н-типа существует поле
![]() ,
которое является поперечным по отношению
к направлению распространенияz,
т.е. результирующий вектор
,
которое является поперечным по отношению
к направлению распространенияz,
т.е. результирующий вектор
![]() колеблется вдоль осиy,
а в декартовой системе координат yz.
колеблется вдоль осиy,
а в декартовой системе координат yz.
Мы рассмотрели
падение плоской электромагнитной волны
с различными поляризациями (горизонтальной
и вертикальной) из воздуха на проводящую
плоскость. Суммарная (результирующая)
волна является результатом интерференции
плоской падающей и отраженной волны, и
уже является не плоской. Таким образом,
проводящую плоскость следует рассматривать
как направляющую плоскость, вдоль
которой распространяются волны Е- и
Н-типов. На границе раздела плоскости
с воздухом выполняются граничные
условия, т.е.
![]() .
.
Классификация направляемых волн
Направляемые электромагнитные волны классифицируют в зависимости от присутствия в них продольных и поперечных составляющих поля. Как правило, за направление распространения волны выбирают ось z. Все направляемые волны классифицируют на следующие типы:
ТЕМ волны или поперечные электромагнитные волны. Такие волны также обозначают ТМ, Т. К ним относятся плоские волны, свободно распространяющиеся в неограниченном пространстве. Ориентация векторов
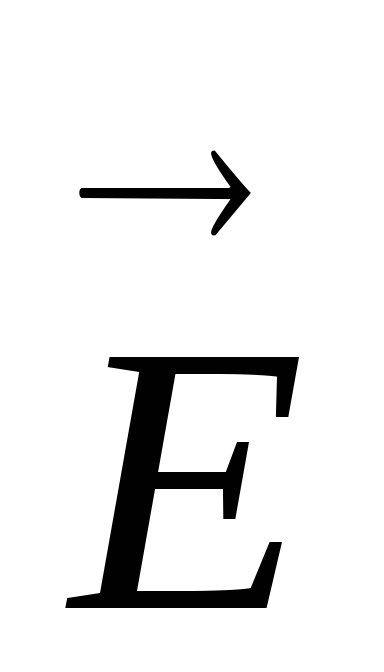 ,
, ,
,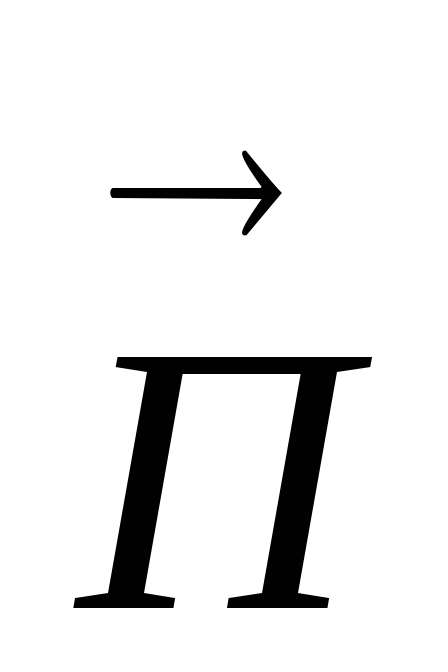 образует правую тройку векторов. В
качестве примера на рис. 4.5 приведены
некоторые варианты структуры ТЕМ волны
при распространении в свободном
пространстве. Учтем связь между
образует правую тройку векторов. В
качестве примера на рис. 4.5 приведены
некоторые варианты структуры ТЕМ волны
при распространении в свободном
пространстве. Учтем связь между ,
,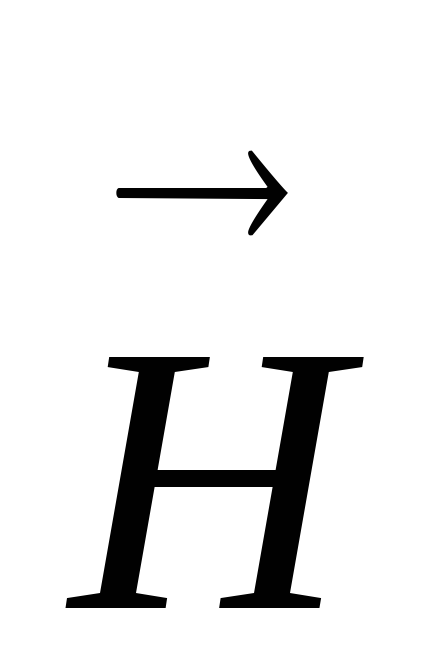 ,
,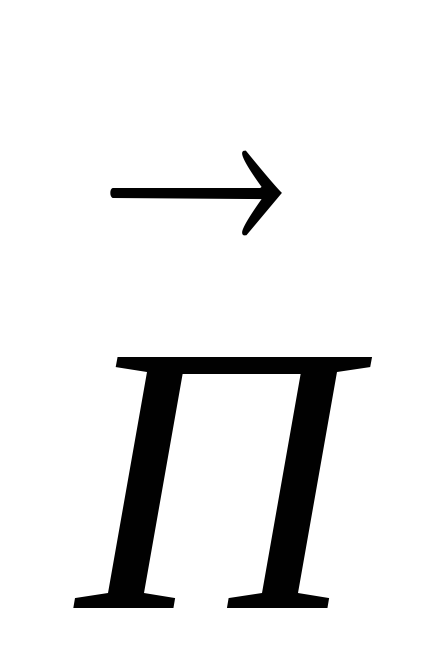 ,
которая выражается формулой
,
которая выражается формулой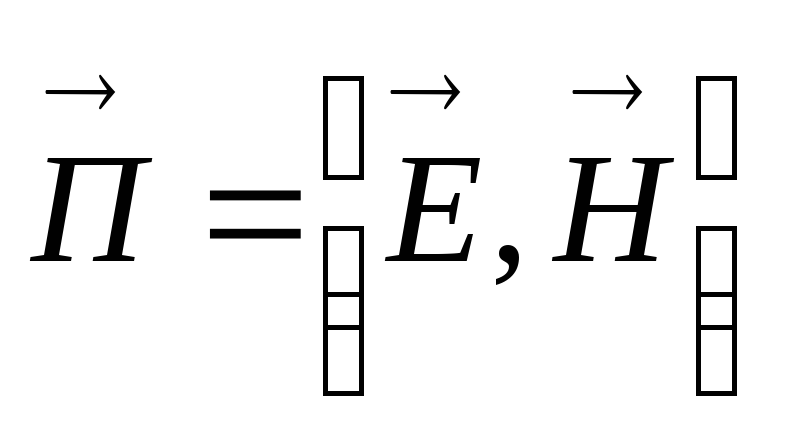

Рис. 4.5
Н-тип волны, или ТЕ-волна (поперечно электрическая). Такие волны содержат и продольные и поперечные составляющие магнитного Н-поля, электрическое поле имеет только перпендикулярную составляющую (
 ).
).Е-тип волны, или ТН-волна (поперечно магнитная). Такие волны содержат одновременно и продольные и поперечные составляющие электрического поля, магнитное поле имеет только поперечную составляющую (
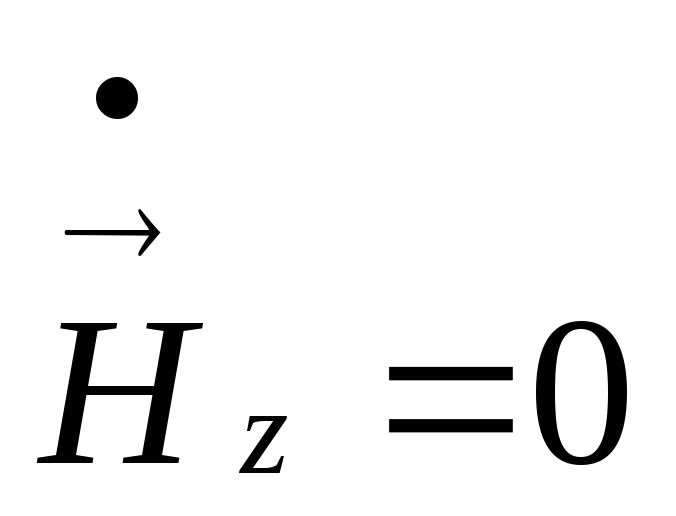 ).
).Гибридные, или смешанные волны. Такие волны одновременно содержат обе продольные составляющие
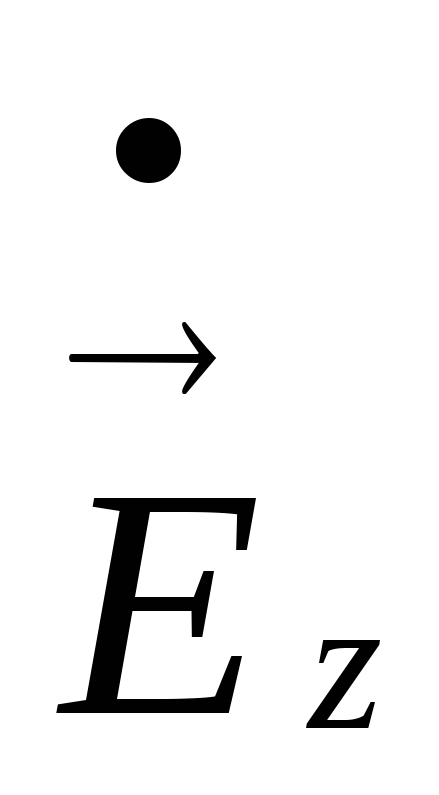 и
и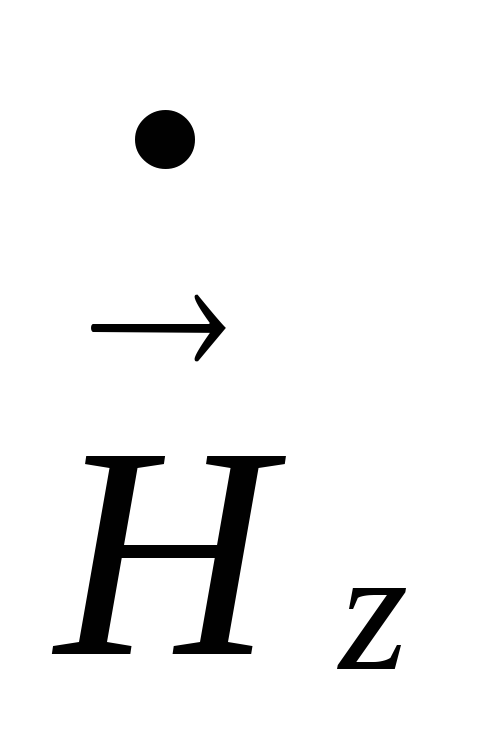 .
.
На границе раздела
двух сред в любой направляющей системе
выполняются граничные условия. Ранее
мы рассмотрели распространение радиоволн
вдоль одной проводящей поверхности.
Для увеличения степени локализации
энергии электромагнитной волны можно
поставить вторую проводящую плоскость,
параллельную первой. Система, состоящая
из двух параллельных плоскостей, будет
действовать, т.е. электромагнитная волна
будет распространяться в пространстве
между плоскостями, если на каждой границе
раздела будут выполняться граничные
условия. Иными словами, и на верхней, и
на нижней плоскости должно выполняться
условие
![]() .
.
На рис. 4.6 показаны некоторые картины силовых линий электромагнитного поля для простейших типов волн, распространяющихся между двумя плоскостями. В каждом примере указан тип волны, распространяющийся в направляющей системе, т.е. между двумя параллельными плоскостями.
 Тип волны
Тип волны
 X
X
 Z
Z
Тип волны
 X
X
 Z
Z
Тип волны
 X
X
 Z
Z
Рис. 4.6
Из рис. 4.6 а, б видно, что один и тот же тип волн различается числом стоячих полуволн, укладывающихся вдоль поперечной координаты х, Это принцип положен в основу классификации одного типа волн.
На рис. 4.6а видно,
что укладывается одна полуволна (одна
замкнутая силовая линия), которую
обозначают с помощью индекса 1, т.е.
![]() .
На рис. 4.6 б показано существование между
двумя плоскостями двух полуволн, что
соответствует волне
.
На рис. 4.6 б показано существование между
двумя плоскостями двух полуволн, что
соответствует волне![]() .
Можно сказать, чтоиндекс
волны
показывает число полуволн, укладывающихся
вдоль поперечной координаты (в нашем
случае - вдоль оси х).
.
Можно сказать, чтоиндекс
волны
показывает число полуволн, укладывающихся
вдоль поперечной координаты (в нашем
случае - вдоль оси х).
Прямоугольный металлический волновод
На практике наиболее часто для передачи электромагнитных волн СВЧ-диапазона используют прямоугольные металлические волноводы, представляющие собой полые металлические трубы прямоугольного сечения. На рис. 4.7 приведено схематичное изображение прямоугольного металлического волновода.
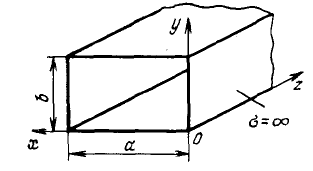
Рис. 4.7
Принято считать, что размеры широкой стенки волновода обозначают а, узкой стенки b. Таким образом, размеры прямоугольного сечения волновода обозначают ахb. Такое обозначение указано в государственном стандарте (ГОСТ).
Размеры волноводов, применяемых в различных диапазонах волн, берутся в справочниках по волноводной технике[ ]. С прямоугольными волноводами связывают прямоугольную декартовую систему координат (x, y, z). Обычно, систему координат размещают так, как показано на рис. 4.7.
Широкое применение полых металлических волноводов обусловлено их следующими достоинствами:
высокая технологичность изготовления;
достаточно малое затухание энергии при распространении волны;
возможность передачи значительных мощностей в импульсном режиме.
Будем полагать,
что внутри волновода находится воздух
или вакуум (=1),
т.е. для такого волновода параметры
среды имеют значения
![]() .
Пусть стенки волновода выполнены из
идеального проводника, т.е. удельная
проводимость
= .
.
Пусть стенки волновода выполнены из
идеального проводника, т.е. удельная
проводимость
= .
В таких волноводах могут распространяться волны Е- и Н-типов. На практике наибольшее распространение получили волны Н-типа, в частности, основной тип волны – волна Н10. Заметим, волна Н-типа для волновода прямоугольного сечения записывается в виде Нmn, где m,n – индексы, указывающие на количество полуволн вдоль оси х и у соответственно.
Исследуем поле Н-волны в прямоугольном волноводе. Напомним, что для такой волны имеется продольные и поперечные составляющие магнитного поля, продольные составляющие электрического поля равны нулю.
Волновое уравнение
для составляющей
![]() имеет вид
имеет вид
![]() (4.1)
(4.1)
Решение уравнения Гельмгольца (4.1) находится в виде
![]()
 ,
(4.2)
,
(4.2)
где h – продольное волновое число.
Волновой процесс происходит и вдоль оси Z и вдоль перпендикулярной плоскости ХОY. Введем соответствующие волновые числа или постоянные распространения:
- постоянная распространения в свободном пространстве,
h - продольное волновое число,
g – поперечное волновое число.
М ежду
волновыми числами существует связь
ежду
волновыми числами существует связь
![]() (4.3)
(4.3)
На основе формулы
(4.3) можно продольное волновое число
выразить в виде
![]() .
Из полученной формулы можно вскрыть
важную особенность, позволяющую понять
процесс распространения волны в
волноводе:
.
Из полученной формулы можно вскрыть
важную особенность, позволяющую понять
процесс распространения волны в
волноводе:
Если >g, то продольное волновое число является вещественным и это означает, что вдоль оси z распространяется бегущая волна;
Если <g, то продольное волновое число h является мнимым и в волноводе не существует распространяющихся колебаний.
В волновом процессе необходимо различать длину волны генератора 0, или длина волны, распространяющуюся в свободном пространстве.
Для описания распространения волны в волноводе введем понятия длину волны в волноводе в, а также критической длины волны кр. Таким образом, следует различать между собой: 0, в, кр.
Критическая длина волны – это наибольшая длина волны, которая может распространяться в волноводе для данного типа колебаний.
С вязь
между волновыми числами и длинами волн
выражается формулами:
вязь
между волновыми числами и длинами волн
выражается формулами:
![]() (4.4)
(4.4)
![]()
 (4.5)
(4.5)

![]() (4.6)
(4.6)
К ритическая
длина волны и длина волны в волноводе
определяются формулами:
ритическая
длина волны и длина волны в волноводе
определяются формулами:
 ,
(4.7)
,
(4.7)
где m, n – соответствующие индексы волны, a, b – размеры волновода.
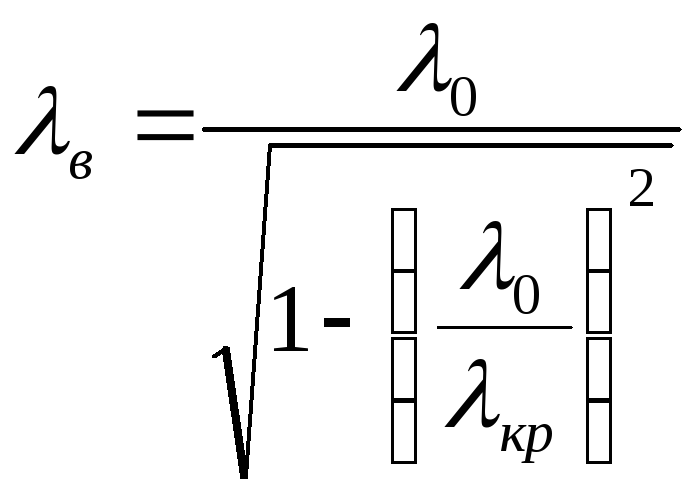 ,
(4.8)
,
(4.8)
где 0 – длина волны генератора, кр – критическая длина волны.
Формулы (4.7) и (4.8) позволяют заключить, что для каждого типа волны при соответствующих размера волновода существует однозначно определенная критическая длина волны. Длина волны, распространяющаяся в волноводе, зависит от длины волны в свободном пространстве и критической длины волны.
Для волны Нmn справедливы формулы:

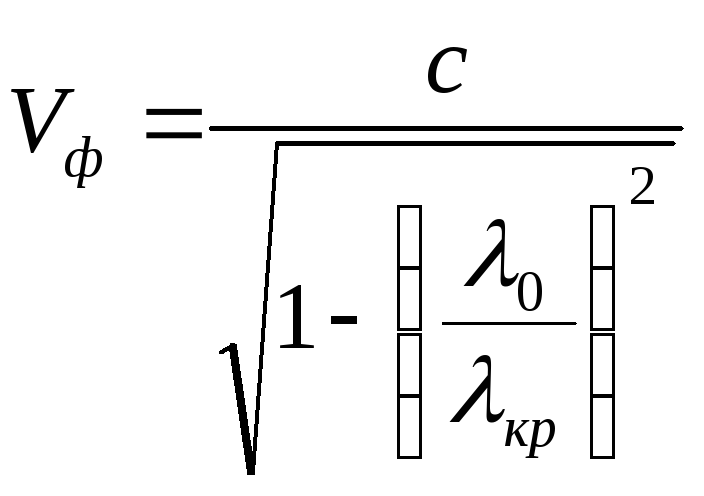 , (4.9)
, (4.9)

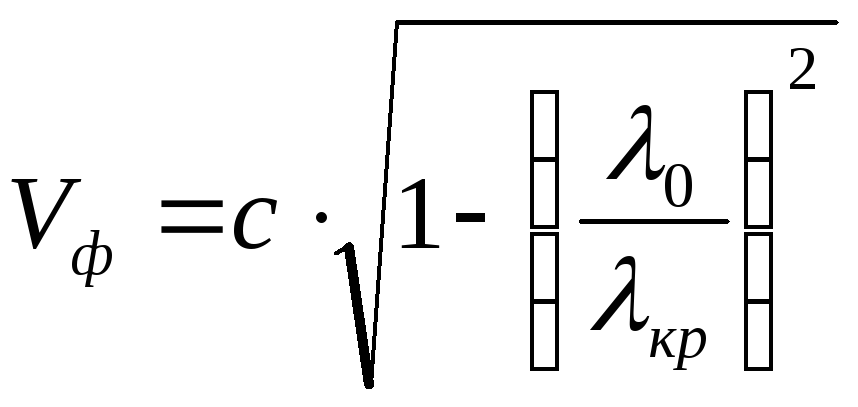 ,
(4.10)
,
(4.10)
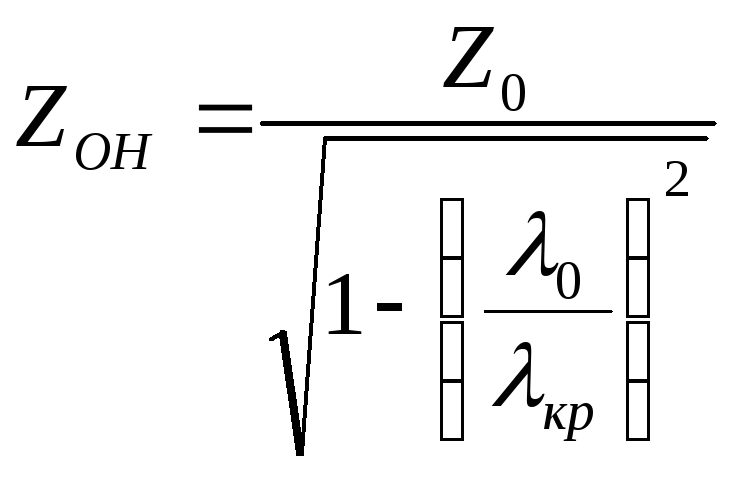
 ,
(4.11)
,
(4.11)
где Vф –фазовая скорость, Vгр – групповая скорость, ZОН – волновое сопротивление для волны Н-типа.
Поле волны Н10 в прямоугольном волноводе
Основным, или низшим, типом волны называется такой тип волны, который обладает наибольшей критической длиной волны при данных размерах волновода. Поперечные размеры волновода для заданной частоты берутся наименьшие.
В прямоугольном волноводе низшим типом волны является волна Н10, учитывая, что a > b. Для такой волны критическая длина имеет значение
![]()
 (4.12)
(4.12)
Передачу энергии по прямоугольному волноводу производят часто с помощью волны Н10. Структура поля волны Н10 описывается формулами.
![]() (4.13)
(4.13)
Поперечное волновое число g определяется формулой
![]()
 (4.14)
(4.14)
Формулы (4.13), описывающие структуру поля волны Н10 можно записать несколько иначе
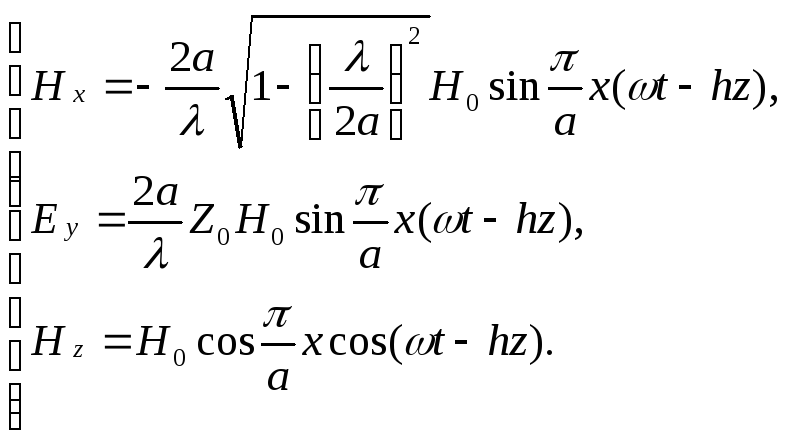 (4.15)
(4.15)
Структура поля волны Н10 приведена на рис. 4.8.
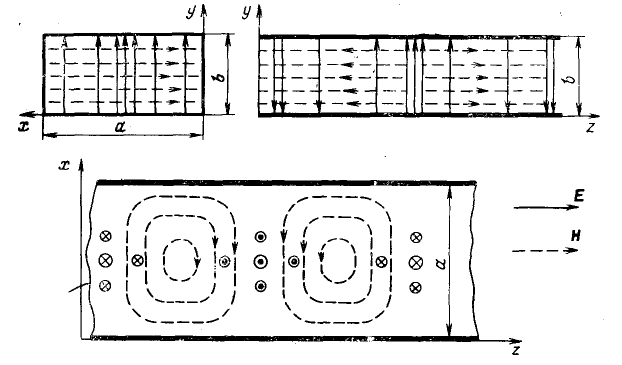
Рис. 4.8
Ф азовая
скорость распространения волны Н10
в волноводе определяется как
азовая
скорость распространения волны Н10
в волноводе определяется как
 (4.16)
(4.16)
Д лина
волны в волноводе отличается от длины
волны в свободном пространстве и
определяется
лина
волны в волноводе отличается от длины
волны в свободном пространстве и
определяется
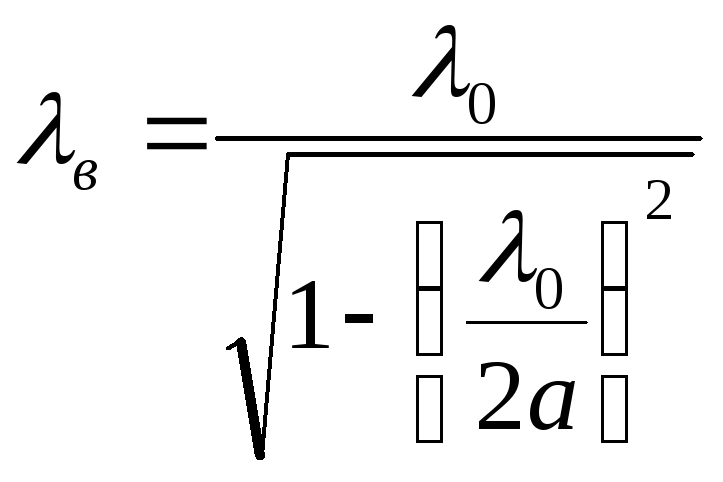 (4.17)
(4.17)
В олновое
сопротивление волновода находится из
формулы
олновое
сопротивление волновода находится из
формулы
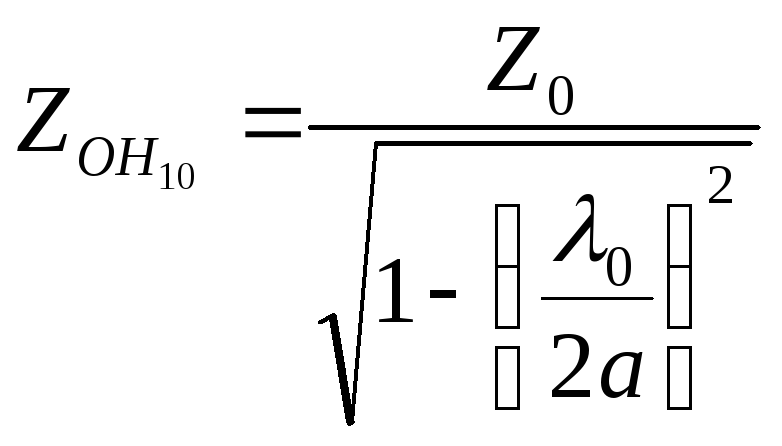 (4.18)
(4.18)
где
Z0
– волновое сопротивление среды,
заполняющей волновод,
![]() .
.
Заметим интересный факт. Магнитное поле, как следует из формул (4.13), (4.15) , имеет две составляющие, амплитуды которых зависят от координат рассматриваемой точки. Эти составляющие сдвинуты в пространстве и времени на 90. Отсюда видно, что магнитное поле волны Н10 имеет эллиптическую поляризацию.
Внутри волновода
выполняются условия для протекания
поверхностного тока
![]() .
Картина поверхностных токов приведена
на рисунке 4.9.
.
Картина поверхностных токов приведена
на рисунке 4.9.
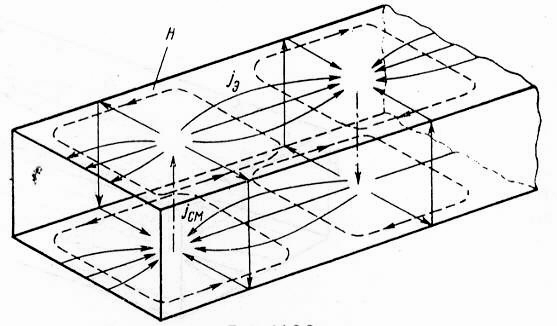
Рис. 4.9
Определим мощность, которая переносится основной волной Н10. значение модуля вектора Пойнтинга определяется
![]() (4.19)
(4.19)
Тогда мощность, переносимая через поперечное сечение проводника с учетом усреднения во времени, определяется формулой

 , (4.20)
, (4.20)
где
![]() - максимальная амплитуда электрического
поля при
- максимальная амплитуда электрического
поля при![]() ,
,
 - волновое
сопротивление прямоугольного волновода
при распространении волны Н10.
- волновое
сопротивление прямоугольного волновода
при распространении волны Н10.
При заданных размерах волновода диапазон рабочих длин волн определяется соотношением
![]() (4.21)
(4.21)
В прямоугольном волноводе также существуют и волны Е-типа, в которых также имеются и продольная и поперечная составляющие поля. Так как волна распространяется вдоль оси z, то уравнение Гельмгольца для составляющей EZ имеет вид
![]() (4.22)
(4.22)
Решением уравнения Гельмгольца с учетом выполнения граничных условий имеет вид
![]() (4.23)
(4.23)
Отметим, что для Е-волн в волноводе можно записать Emn, где индексы m, n определяют конкретную структуру поля. Для Е-волн ни одно из чисел m, n не может быть равно нулю, в противном случае составляющая EZ=0, следовательно и другие составляющие поля обратятся в нуль. Таким образом, волны Е-типа в прямоугольном волноводе вида Е0n и Em0 не существуют.
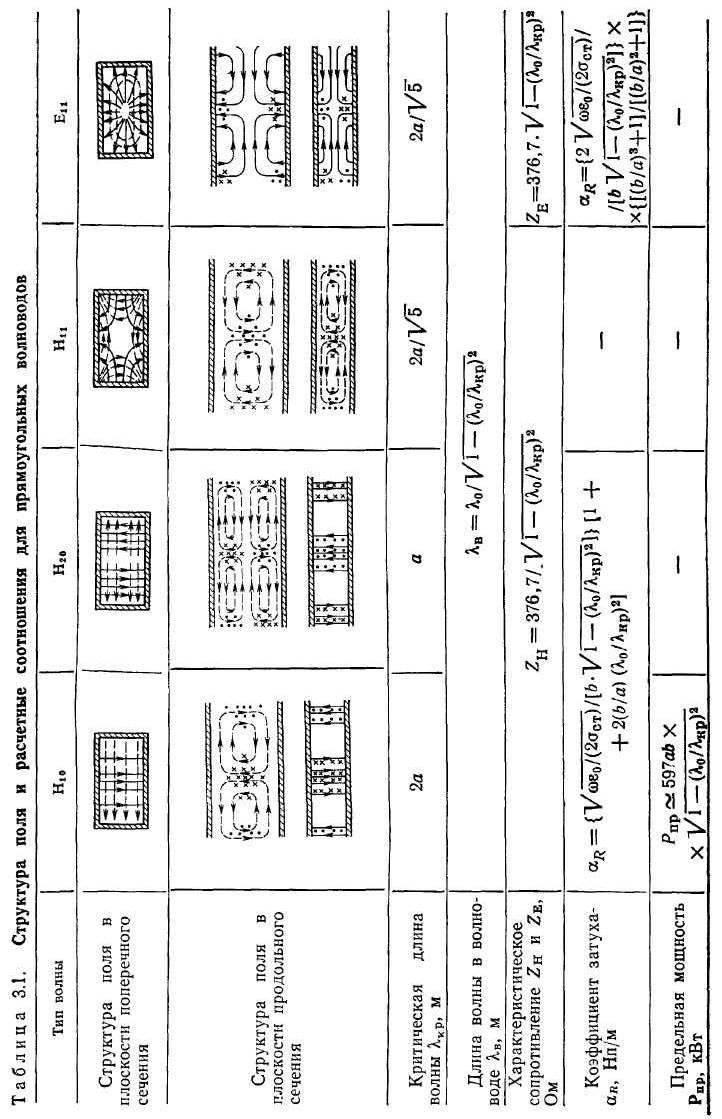
В таблице 4.1 показана структура поля волн Е- и Н-типа в прямоугольном волноводе, также приведены формулы, определяющие их основные характеристики.
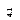

Приведем пример расчета параметров волны, при ее распространении в прямоугольном волноводе .
Прямоугольный
волновод, заполненный воздухом, имеет
поперечное сечение
![]()
![]() .
.
Определить
все типы волн, которые могут существовать
в волноводе при частоте 5000 МГц. Для
основной волны и для волны с наиболее
высокими значениями
![]() и
и![]() найти критическую длину волны в волноводе,
фазовую и групповую скорости.
найти критическую длину волны в волноводе,
фазовую и групповую скорости.
Решение.
1. Определяем длину волны в свободном пространстве:
![]()
Зная,
что скорость света с=3108
м/с находим
![]() м.
м.
2. Критическую длину волны в волноводе определяем по формуле:
 .
.
По волноводу могут
распространяться волны, которые
удовлетворяют условию
![]() ,
или в нашем случае
,
или в нашем случае
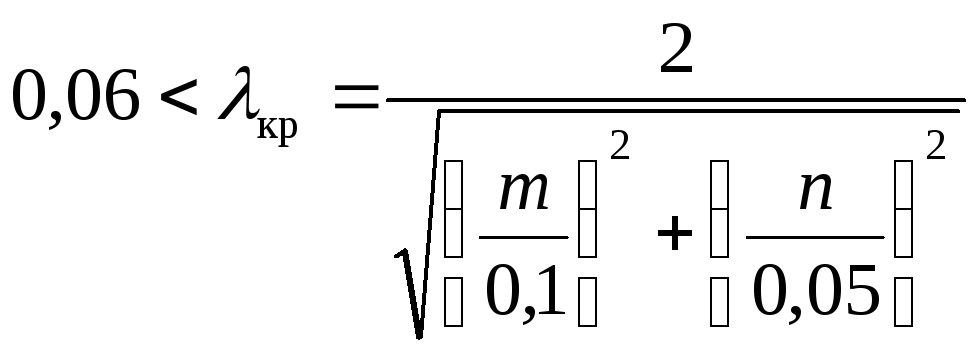
Придавая
![]() и
и![]() целые значения, найдём искомые типы
волн. Так, при
целые значения, найдём искомые типы
волн. Так, при![]() и
и![]() получим
получим![]() м, т.е. в волноводе может существовать
волна типа
м, т.е. в волноводе может существовать
волна типа![]() .
Аналогично определяем, что по волноводу
могут распространяться также волны
типа
.
Аналогично определяем, что по волноводу
могут распространяться также волны
типа![]() и
и![]() .
Других типов волн в волноводе быть не
может. Действительно, пусть
.
Других типов волн в волноводе быть не
может. Действительно, пусть![]() и
и![]() .
Тогда получим
.
Тогда получим
![]() ,
,
т.е. требуемое
неравенство не соблюдается. Для волн
типа
![]() и
и![]() находим длину волны в волноводе, её
фазовую и групповую скорости. Для волн
типа
находим длину волны в волноводе, её
фазовую и групповую скорости. Для волн
типа![]() ( или Н10)
имеем:
( или Н10)
имеем:
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
Для волны типа
![]() находим:
находим:![]()
![]() ;
;![]() ,
,![]()
![]() ,
,![]()
![]() .
.
Круглые волноводы
Способы возбуждения волны Н-типа в прямоугольном волноводе
Возбуждением волновода называется создание в нем высокочастотного электромагнитного поля. Для этого необходимо непосредственно от генератора ввести в рассматриваемый волновод электромагнитную энергию из кабеля или другого волновода. Устройство, служащее для этой цели, называют элементом связи или возбудителем.
Связь волновода с источником осуществляется различными способами (рис. 4.10).
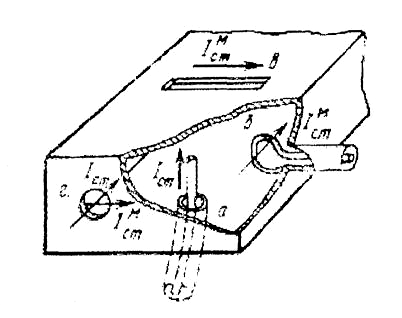
Рис. 4.10
Если СВЧ-генератор имеет коаксиальный выход, то он заканчивается в волноводе штыревой антенной (а) или петлей (б); некоторые типы клистронов также имеют выход в виде штыря, погружаемого в волновод. Связь волновода с генератором и связь между волноводами может осуществляться с помощью щелей (в) и отверстий (г), прорезанных в их стенках.
При возбуждении
в прямоугольном волноводе волны типа
Н10
штырем, тонкий штырь длиной l
расположен параллельно оси y
на расстоянии![]() от закороченного конца волновода и
от закороченного конца волновода и![]() от его боковой стенки (рис. 4.11), где h и q
от его боковой стенки (рис. 4.11), где h и q
Рис. 4.11
Круглые волноводы
Круглый волновод представляет собой полый цилиндр радиусом a. Схематическое изображение круглого волновода показано на рис. 4.12.
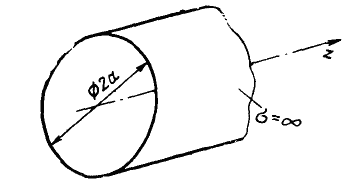
Рис. 4.12
Приведем основные результаты решения волновых уравнений для круглого волновода. В круглом волноводе существуют волны Е и Н-типов.
Фазовая и групповая скорости определяются следующим образом.
Для волн Е-типа:
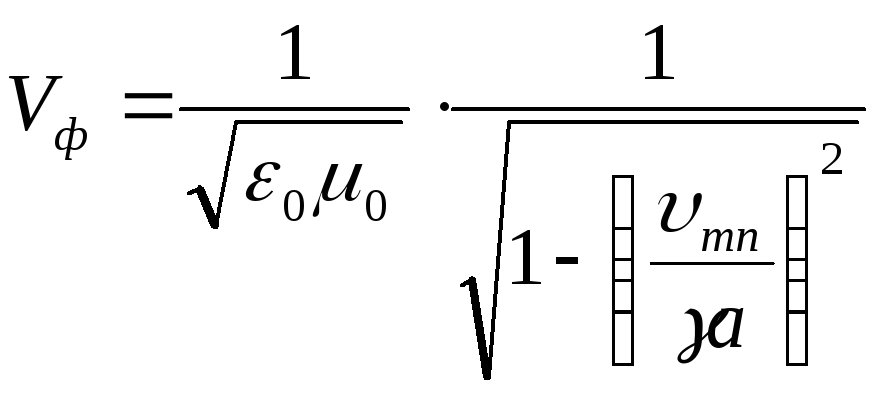

 (4.24)
(4.24)
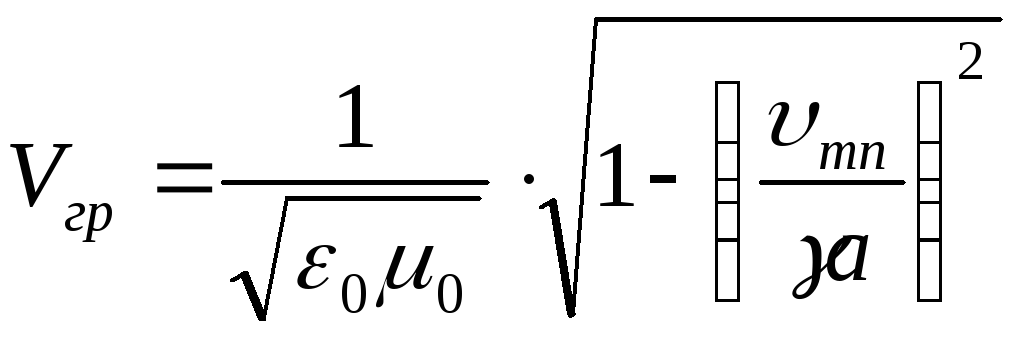 (4.25)
(4.25)
![]()
 (4.26)
(4.26)
где
![]() - волновое число,
- волновое число,![]() - корни уравнения Бесселя, а – радиус
волновода.
- корни уравнения Бесселя, а – радиус
волновода.
Д ля
волны Н-типа:
ля
волны Н-типа:
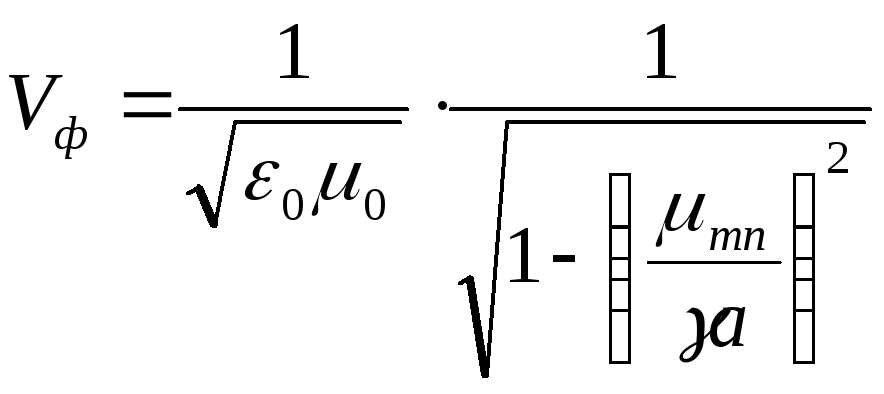 (4.27)
(4.27)
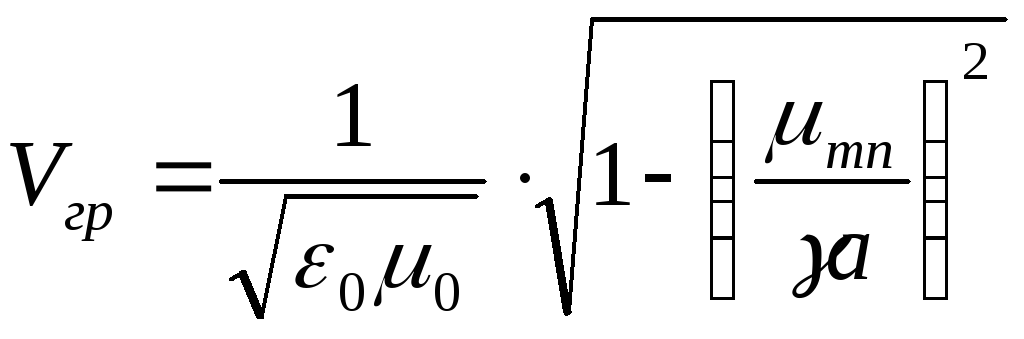
 (4.28)
(4.28)
![]()
 (4.29)
(4.29)
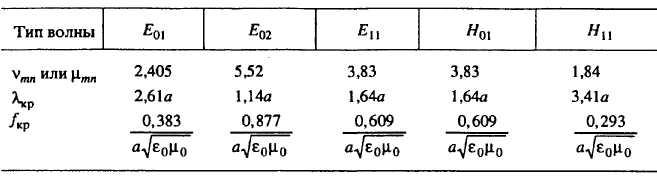
В таблице 4.2
приведены значения корней функции
Бесселя
![]() и их производных, а также формулы
критической длины волны и критической
частоты для некоторых типов волн.
и их производных, а также формулы
критической длины волны и критической
частоты для некоторых типов волн.
Таблица 4.2 Значения корней функции Бесселя
Основные формулы и структура поля для некоторых волн Е- и Н-типа в круглом волноводе показаны в таблице 4.3 .
Таблица 4.3 Основные формулы и структура поля в круглом волноводе.
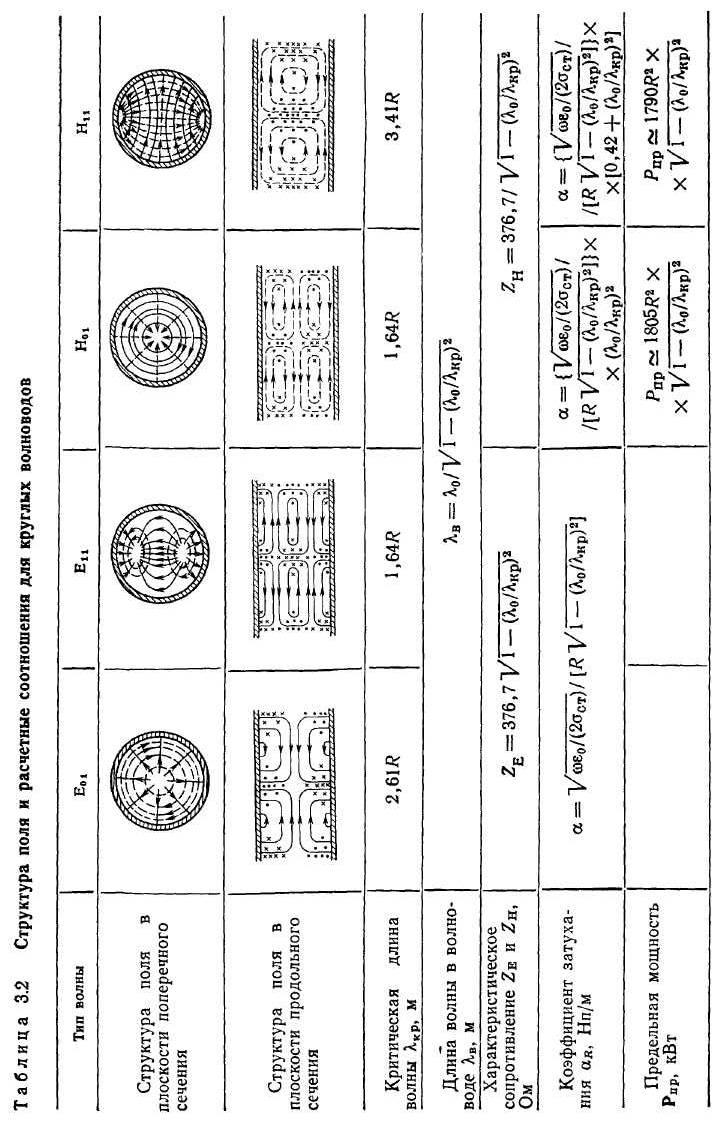

Анализ содержания таблицы 4.2, 4.3 позволяет сделать следующие выводы:
В круглом волноводе низшим типом волны является волна Н11.
У волны Н01 на стенках волновода азимутная составляющая отсутствует и существует только продольная составляющая напряженности магнитного поля. Продольная составляющая поля при
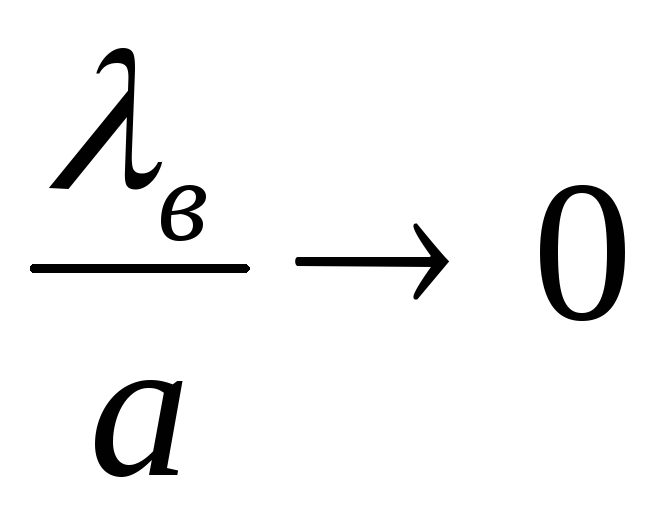 также стремится к нулю, что приводит
к результату: ток по стенкам не течет.
Этим обеспечивается малое затухание
волны Н01
(Н0n)
в круглых волноводах.
также стремится к нулю, что приводит
к результату: ток по стенкам не течет.
Этим обеспечивается малое затухание
волны Н01
(Н0n)
в круглых волноводах.Волна Е01 в круглом волноводе обладает круговой симметрией. Благодаря этому свойству она используется во вращающихся соединениях антенных устройств.
По поверхности круглого волновода протекают также поверхностные токи. На рис. 4.13 показана схема поверхностных токов для волн Н11 и Н01.
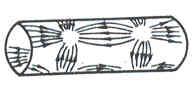
Рис. 4.13
Коаксиальные волноводы
Коаксиальный волновод представляет собой систему, состоящую из двух соосных металлических цилиндров, разделенных слоем диэлектрика. На рисунке 4.14а приведено схематическое изображение коаксиального волновода.

Рис. 4.14
Диаметр внутреннего цилиндра на рису. 4.14 обозначен d, внешнего – D.
К основным достоинствам коаксиальных линий передачи относятся следующие:
Широкополосность, т.е. способность пропускать широкую полосу рабочих частот;
Электромагнитное поле, имеющее структуру ТЕМ-волны, распространяется в пространстве между цилиндрами и во внешнюю среду волна не выходит, т.е. отсутствует паразитное излучение;
Возможность изготовления в виде гибких коаксиальных кабелей.
Благодаря таким достоинствам, коаксиальные волноводы нашли широкое применение, чаще всего их используют для соединения узлов и блоков радиоаппаратуры. Такие волноводы применяются как в метровом, так и в сантиметровом диапазахъ, обычно не выше 20 ГГц. Хотя в некоторых случаях они могут использоваться и на более высоких частотах в виде коротких отрезков. Незначительная длина волноводов в таких случаях обусловлена большим затуханием, составляющим более 1дБ/м.
Коаксиальные кабели изготавливают в виде жестких и гибких конструкций. Установлено, что по коаксиальному кабелю могут передаваться волны любых частот, включая частоту постоянного тока. Структура поля электромагнитной волны соответствует типу ТЕМ, т.е. EZ=0, НZ=0.
При изучении распространения электромагнитной волны вдоль коаксиальной линии передачи применяют цилиндрическую систему координат, которая, как известно, задается углом , радиусом r, и координатой z, т.е. (r, , z).
На рис. 4.14б показана
структура ТЕМ волны, распространяющейся
внутри коаксиального кабеля. Напряженность
электрического поля имеет только одну
радиальную составляющую, т.е. векторы
![]() направлены по радиусам в плоскости
поперечного сечения. Магнитное поле
содержит также одну составляющую Н,
силовые линии магнитного поля расположены
в виде концентрических окружностей
вокруг внутреннего провода (вокруг оси
z).
направлены по радиусам в плоскости
поперечного сечения. Магнитное поле
содержит также одну составляющую Н,
силовые линии магнитного поля расположены
в виде концентрических окружностей
вокруг внутреннего провода (вокруг оси
z).
Значения напряженностей магнитного и электрического поля определяются формулами:
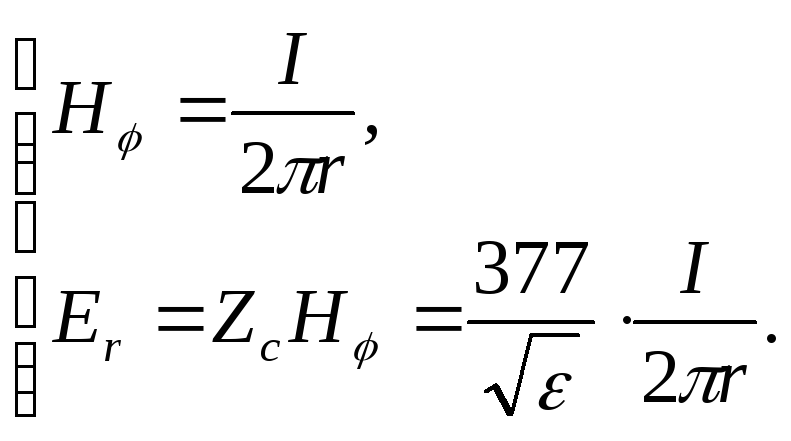
 (4.30)
(4.30)
где r – радиус, I – сила протекающего тока, Zc – волновое сопротивление среды, заполняющей пространство между цилиндрами, - относительная диэлектрическая проницаемость.
Напряженность электрического поля можно также записать в виде
![]() (4.31)
(4.31)
Отметим, что рабочий диапазон частот коаксиальных линий передачи энергии ограничен только со стороны высоких частот тем фактом, что при высоких частотах возможно возбуждение высших типов волн. Для коаксиальной линии ближайшим высшим типом волны является волна Н11, структура которой является сходной со структурой Н11 в круглом волноводе.
Для волны Н11 критическая длина волны определяется формулой
![]()
 ,
(4.32)
,
(4.32)
где D – диаметр большого цилиндра, d – диаметр малого цилиндра.
Из формулы (4.32) видно, что высшие типы волн появляются тогда, когда длина волны возбуждающих колебаний становится меньше полусуммы периметров проводников. Таким образом, минимальная длина волны, распространяющаяся в коаксиальном волноводе, определяется формулой
![]() (4.33)
(4.33)
Дальнейшее уменьшение размеров ограничено. Такое ограничение связано с увеличением тепловых потерь, уменьшением электрической прочности и усложнением технологии изготовления.
Для коаксиальной линии расчет напряжения и волнового сопротивления производится по формулам
 (4.34)
(4.34)
![]() (4.35)
(4.35)
Пробивное напряжение коаксиального волновода определяется формулой
![]() ,
(4.36)
,
(4.36)
где
![]() - предельная (максимальная) напряженность
поля.
- предельная (максимальная) напряженность
поля.
Для коаксиального
волновода с воздушным заполнением
![]() .
Тогда напряжение пробоя
.
Тогда напряжение пробоя![]() .
Максимум пробивного напряжения
соответствует соотношению
.
Максимум пробивного напряжения
соответствует соотношению![]() ,
при этом волновое сопротивление
,
при этом волновое сопротивление
![]() Ом.
Ом.
Предельная мощность, которая может передаваться по коаксиальному волноводу, определяется соотношением
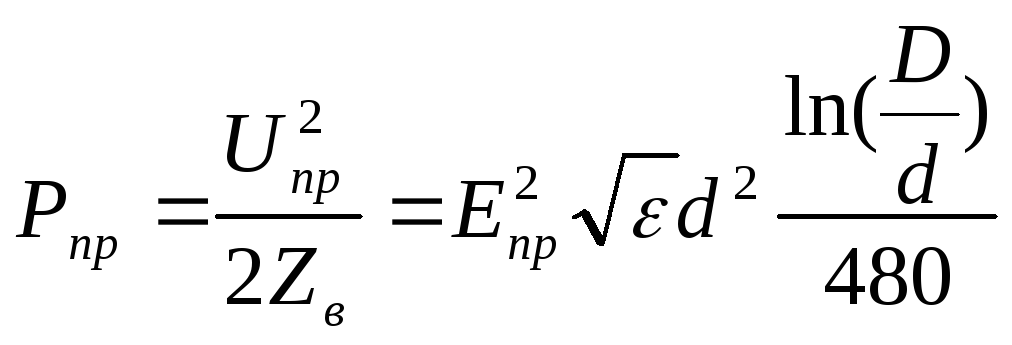 (4.37)
(4.37)
Затухание волны в коаксиальном кабеле вызвано потерями энергии, обусловленными тепловыми потерями в проводнике, а также потерями в диэлектрике.
Так, для коаксиальной линии с медными проводниками потери можно рассчитать, исходя из формулы
 ,
дБ/м , (4.38)
,
дБ/м , (4.38)
где - относительная диэлектрическая проницаемость, f – линейная частота, D, d – диаметры соответственно внешнего и внутреннего цилиндрических проводников.
Минимальное
затухание в коаксиальной линии передачи
энергии достигается при
![]() ,
что соответствует волновому сопротивлению
,
что соответствует волновому сопротивлению![]()
Стандартные значения волновых сопротивлений применяемых коаксиальных кабелей соответствуют 50 и 75 Ом.
Однопроводная линия передачи [ ]
Рассмотрим распространение электромагнитной волны вдоль одинарного проводника, покрытого тонким слоем диэлектрика. Такая линия называется однопроводной линией передачи, или линией поверхностной волны (ЛПВ), или линией Губо. Теория линии Губо разработана давно, но практического широкого применения ЛПВ не нашла. Очередной интерес к ЛПВ связан с реализацией возможности ее применения для построения антенных решеток жестких и гибких конструкций с высокой технологичностью изготовления и удовлетворяющих заданным требованиям.
Волноводы линии
поверхностной волны (ЛПВ) могут быть
успешно использованы для наземных линий
передачи СВЧ-энергии на расстоянии
![]()
![]() .
.
ЛПВ состоит из цилиндрического проводника 3, покрытого слоем диэлектрика 1, который граничит с воздушным пространством 2.
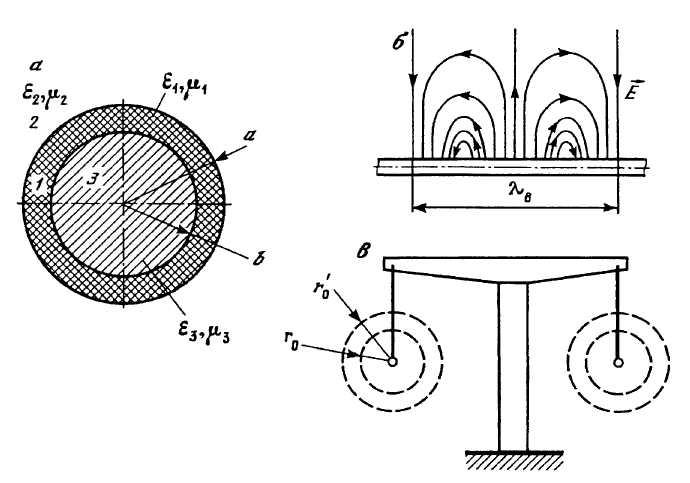
![]() - поперечное сечение
волновода;
- поперечное сечение
волновода;
![]() - топография электрического поля;
- топография электрического поля;![]() - трассировка линии
- трассировка линии
Рис.4.15.
Основной волной
ЛПВ является волна
![]() ,
обладающая круговой симметрией и
нормированным поперечным волновым
коэффициентом
,
обладающая круговой симметрией и
нормированным поперечным волновым
коэффициентом![]() Топография электрического поля вокруг
стержня ЛПВ приведена также на рис.
4.15б.
Топография электрического поля вокруг
стержня ЛПВ приведена также на рис.
4.15б.
Коэффициент затухания ЛПВ, обусловленный потерями в медном проводнике, определяется как
![]()
![]() (4.39)
(4.39)
а коэффициент затухания, обусловленный диэлектрик,
![]()
![]() ,
(4.40)
,
(4.40)
где
![]() - частота, МГц,
- частота, МГц,![]() - сопротивление ЛПВ, Ом,
- сопротивление ЛПВ, Ом,![]() - радиус проводника,
- радиус проводника,![]() .
.
Параметр
![]() ,
где
,
где![]() - фазовая скорость поверхностной волны,
определяется из трансцендентного
уравнения
- фазовая скорость поверхностной волны,
определяется из трансцендентного
уравнения
![]() ,
(4.41)
,
(4.41)
а волновое сопротивление ЛПВ
 (4.42)
(4.42)
Рассмотрим ЛПВ,
собранную из медного проводника радиусом
![]()
![]() ,
покрытого слоем полиэтилена
,
покрытого слоем полиэтилена![]() с наружным радиусом
с наружным радиусом![]()
![]() и тангенсом диэлектрических потерь
и тангенсом диэлектрических потерь![]() ,
работающую на частоте 915
,
работающую на частоте 915![]()
![]() .
При заданных условиях по уравнению
(4.41) можно найти параметр
.
При заданных условиях по уравнению
(4.41) можно найти параметр![]() и определить относительную фазовую
скорость волны в ЛПВ
и определить относительную фазовую
скорость волны в ЛПВ![]() ,
которая указывает на незначительное
замедление.
,
которая указывает на незначительное
замедление.
Волновое сопротивление
рассматриваемой ЛПВ, согласно (4.42), равно
![]()
![]() ,
что позволяет вычислить по (4.39), (4.40)
коэффициенты затухания
,
что позволяет вычислить по (4.39), (4.40)
коэффициенты затухания![]()
![]()
![]() и
и![]()
![]()
![]() .
Полный коэффициент затухания
.
Полный коэффициент затухания![]()
![]() и он может быть доведён до
и он может быть доведён до![]()
![]() при увеличении диаметра проводника
при увеличении диаметра проводника![]() до
до![]()
![]() .
Таким образом, ЛПВ пригодна для передачи
СВЧ-мощности на километровые расстояния.
.
Таким образом, ЛПВ пригодна для передачи
СВЧ-мощности на километровые расстояния.
Трасса прокладки ЛПВ должна быть свободна от посторонних поглощающих и отражающих предметов, в том числе удалена от поверхности Земли на расстояние
![]()
 (4.43)
(4.43)
являющееся
радиусом цилиндра, в котором распространяется
95% передаваемой мощности, причём в
рассмотренном выше случае
![]() и
и![]()
![]() .
Практическая ЛПВ может быть проложена
на опорах с помощью тефлоновых подвесов,
длина которых обеспечивает расстояние
линии от перекладины опоры не менее
.
Практическая ЛПВ может быть проложена
на опорах с помощью тефлоновых подвесов,
длина которых обеспечивает расстояние
линии от перекладины опоры не менее![]() ,
а длина перекладины соответствует
расстоянию линии от опоры
,
а длина перекладины соответствует
расстоянию линии от опоры![]() .
При возможности свободное пространство
вокруг ЛПВ должно иметь радиус
.
При возможности свободное пространство
вокруг ЛПВ должно иметь радиус![]()
![]() ,
соответствующий кругу, в котором
сконцентрировано более 99% передаваемой
мощности.
,
соответствующий кругу, в котором
сконцентрировано более 99% передаваемой
мощности.
Максимально допустимая мощность, передаваемая ЛПВ, определяется пробивной напряжённостью воздуха, окружающего слой диэлектрика, и равна
![]() (4.44)
(4.44)
что
при
![]()
![]() ,
,![]()
![]() ,
,![]() и
и![]()
![]() даёт
даёт![]()
![]() .
При передаче по ОЛП мегаваттных уровней
мощности следует учесть потери мощности
в ней и обеспечить её обдув окружающим
воздухом для охлаждения.
.
При передаче по ОЛП мегаваттных уровней
мощности следует учесть потери мощности
в ней и обеспечить её обдув окружающим
воздухом для охлаждения.
Открытая поверхностная
волна ЛПВ, заключённая внутри цилиндра
радиусом
![]() ,
может быть частично перехвачена приёмной
антенной и использована для технологических
и транспортных целей.
,
может быть частично перехвачена приёмной
антенной и использована для технологических
и транспортных целей.
Полосковые линии передачи электромагнитной энергии
Полосковая линия передачи энергии – это линия передачи, содержащая токопроводящие элементы в виде одной или нескольких металлических полосок, нанесенных на диэлектрике, лежащем на металлическом экране. На рис. 4.16 показаны виды полосковых линий: симметричная(рис. 4.16а) и несимметричная (рис. 4.16б).
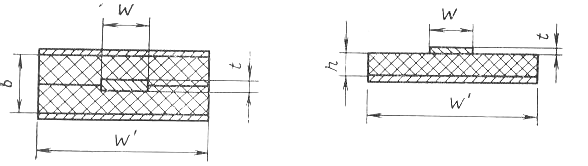
а) б)
Рис. 4.16
t – толщина проводника, W – ширина проводника, W/ – ширина основания, h – толщина диэлектрика, b – толщина диэлектрика в симметричной полосковой линии.
Чаще всего металлические полоски наносят на диэлектрик методом планарной технологии (фотолитография, напыление и др.).
Полосковые линии
применяются в диапазоне частот
![]() .
Предельная передаваемая мощность
зависит от режима работы: в непрерывном
режиме – несколько десятков ватт, в
импульсном – несколько кВт.
.
Предельная передаваемая мощность
зависит от режима работы: в непрерывном
режиме – несколько десятков ватт, в
импульсном – несколько кВт.
Полосковые линии широко применяются на практике. К достоинствам таких линий передачи энергии относятся следующие:
широкополосность;
малые габаритные размеры;
незначительная масса;
возможность применения потного монтажа;
легко осуществить автоматизацию процесса;
малая стоимость изготовления.
В общем случае, в полосковых линиях передачи можно возбудить большое количество волн различных типов. Возбуждение типа волны зависит от конструкции устройства возбуждения, наличие неоднородностей, потерь, конструкции самой линии.
Металлический
экран полосковой линии выполняют часто
в виде прямоугольника с размерами axb,
где a
– ширина, b
– высота. Причем, чтобы исключить
возбуждение низших типов волн, необходимо
соблюдать соотношения
![]() ,
,![]() ,
где
,
где![]() - длина волны в волноводе (линии).
- длина волны в волноводе (линии).
В структуре поля значительно преобладание ТЕМ-волны. Волновое сопротивление для ТЕМ-волны определяется
![]() ,
(4.45)
,
(4.45)
где
С – погонная емкость,
![]() - фазовая скорость,
- фазовая скорость,![]() - эффективная диэлектрическая
проницаемость.
- эффективная диэлектрическая
проницаемость.
Реально волновое
сопротивление принимает значения ![]() .
.
Эффективная диэлектрическая проницаемость определяется для ТЕМ-волны экспериментально и вычисляется по формуле
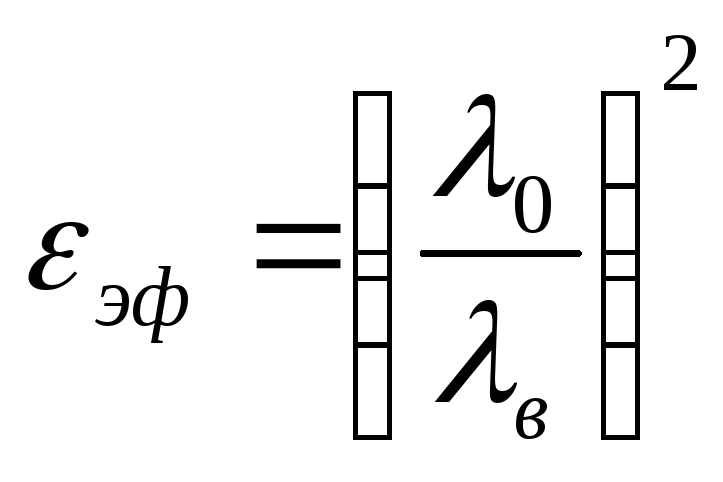 ,
(4.46)
,
(4.46)
где
![]() - длина волны в свободном пространстве,
- длина волны в свободном пространстве,![]() - длина волны в полосковой линии.
- длина волны в полосковой линии.
Потери в диэлектрике определяются коэффициентом
![]() (4.47)
(4.47)
Коэффициент затухания, учитывающий потери в диэлектрике, а также потери, связанные с излучением, определяют, как правило, экспериментально.
Объемные резонаторы.
Резонатор – это колебательная система, способная накапливать энергию колебаний или волн при воздействии внешней силы определенной частоты.
В СВЧ технике используют объемные резонаторы двух видов: полый металлический и диэлектрический. Резонаторы используют в фильтрах различного назначения, измерительных приборах, в качестве колебательных систем электронных приборов.
Если внутри резонатора возникло электромагнитное поле, то происходит непрерывный обмен энергией между электрическим и магнитным полем. Для каждой частоты в резонаторе возникает определенная структура поля. Таким образом, в резонаторе можно возбудить по отдельности спектр частот, каждому из которых соответствует своя структура поля.
Структура поля, соответствующая минимальной частоте, называется низшим типом колебаний. Возможны случаи, когда резонансные частоты двух или более видов колебаний с различными структурами совпадают, то такие колебания называются вырожденными.
Основные параметры резонаторов.
Свойства резонатора описываются следующими основными параметрами:
резонансная частота
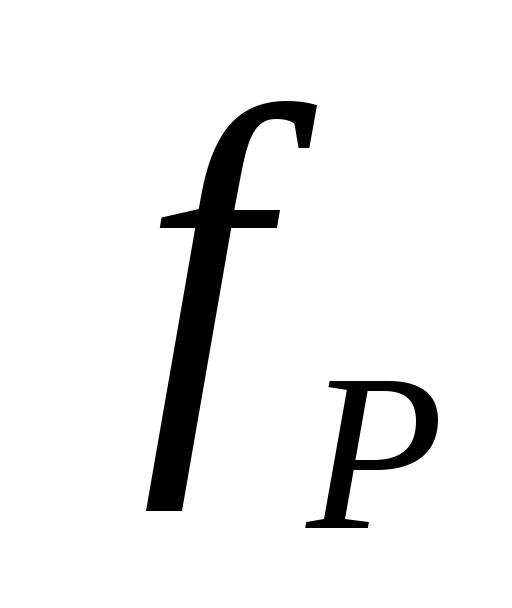 - это частота, на которой амплитуда
колебаний достигает наибольшего
значения при прочих равных условиях;
- это частота, на которой амплитуда
колебаний достигает наибольшего
значения при прочих равных условиях;добротность Q – это отношение резонансной частоты к ширине полосы частот
![]() (4.48)
(4.48)
где
![]() -ширина полосы
пропускания резонатора;
-ширина полосы
пропускания резонатора;
коэффициент связи
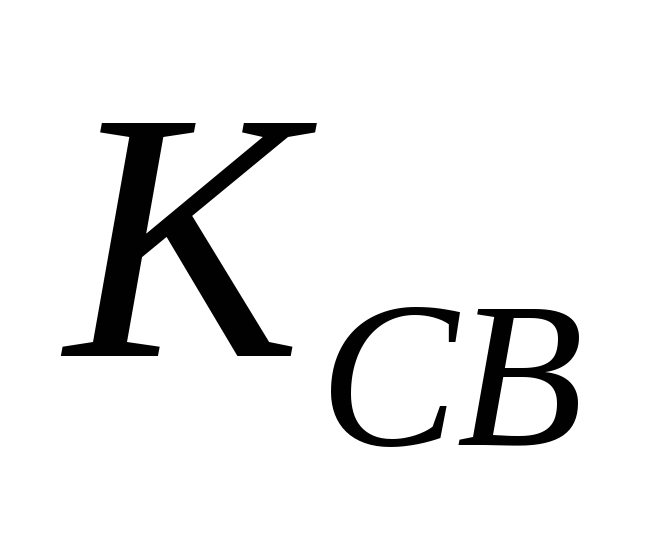 - это отношение мощности, передаваемой
резонатором во внешнюю цепь
- это отношение мощности, передаваемой
резонатором во внешнюю цепь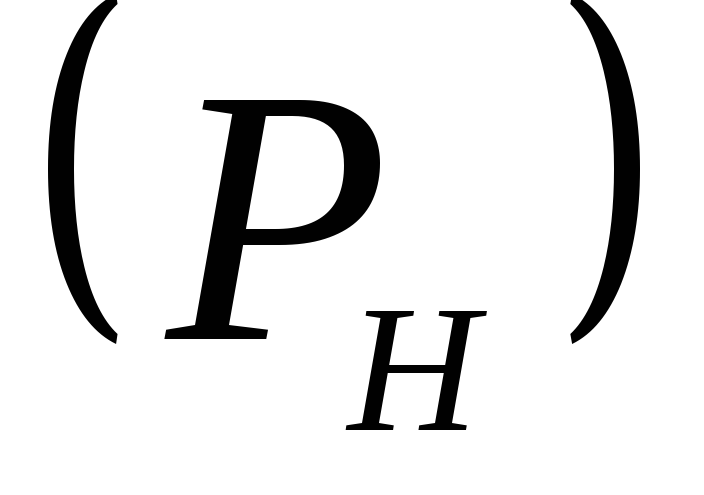 к мощности потерь на резонансной частоте
к мощности потерь на резонансной частоте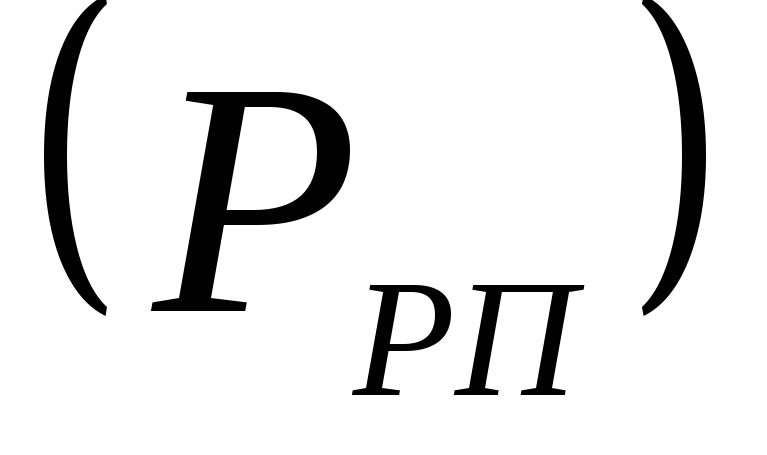
![]() (4.49)
(4.49)
Нахождение резонансных частот в объемном резонаторе.
Явление резонанса в объемном резонаторе наступает в случае, когда на данной частоте энергия электрического поля равна энергии магнитного поля. Математически равенство энергии полей выражается в виде:
![]() (4.50)
(4.50)
где
![]() -амплитудные
значения, соответственно, электрического
и магнитного полей, V
– объем, занимаемый полем в резонаторе,
-амплитудные
значения, соответственно, электрического
и магнитного полей, V
– объем, занимаемый полем в резонаторе,
![]() - абсолютная диэлектрическая и магнитная
проницаемость среды, заполняющей
резонатор.
- абсолютная диэлектрическая и магнитная
проницаемость среды, заполняющей
резонатор.
Первое уравнение Максвелла, как хорошо всем известно, имеет вид:
![]()
где
![]() -амплитуда
напряженности электрического и магнитного
полей, w
– циклическая частота,
-амплитуда
напряженности электрического и магнитного
полей, w
– циклическая частота, ![]() - абсолютная диэлектрическая проницаемость,
- абсолютная диэлектрическая проницаемость,
![]() -комплекснаяабсолютная
диэлектрическая проницаемость, σ
– удельная проводимость вещества.
-комплекснаяабсолютная
диэлектрическая проницаемость, σ
– удельная проводимость вещества.
Учитывая условие появления резонанса (4.50) и первое уравнение Максвелла, определим собственную частоту колебаний резонатора.
Из первого уравнения Максвелла выразим напряженность электрического поля:
![]() .
(4.51)
.
(4.51)
Далее подставим уравнение (4.51) в формулу (4.50) и получим:
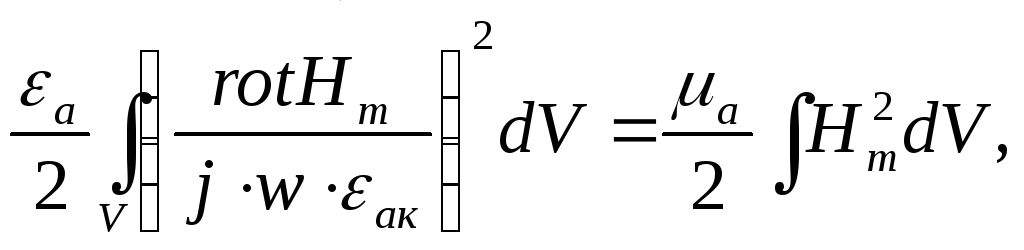
или запишем
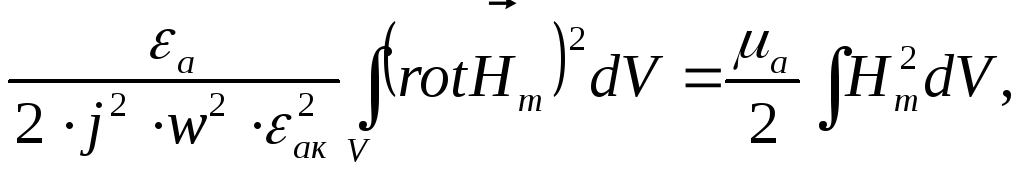
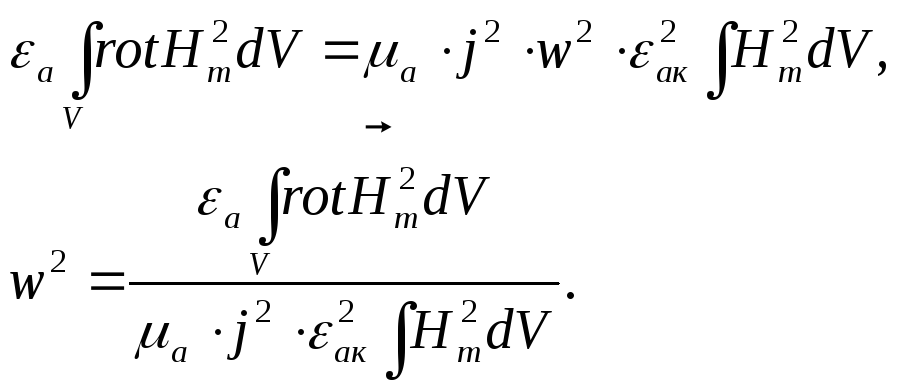
Е сли
среда, заполняющая резонатор, не обладает
проводящими свойствами, то
сли
среда, заполняющая резонатор, не обладает
проводящими свойствами, то![]() .
Кроме того, физически циклическая
частота может принимать положительные
значения, поэтому необходимо взять
модуль полученного отношения. Учитывая
сказанное выше, получим:
.
Кроме того, физически циклическая
частота может принимать положительные
значения, поэтому необходимо взять
модуль полученного отношения. Учитывая
сказанное выше, получим:
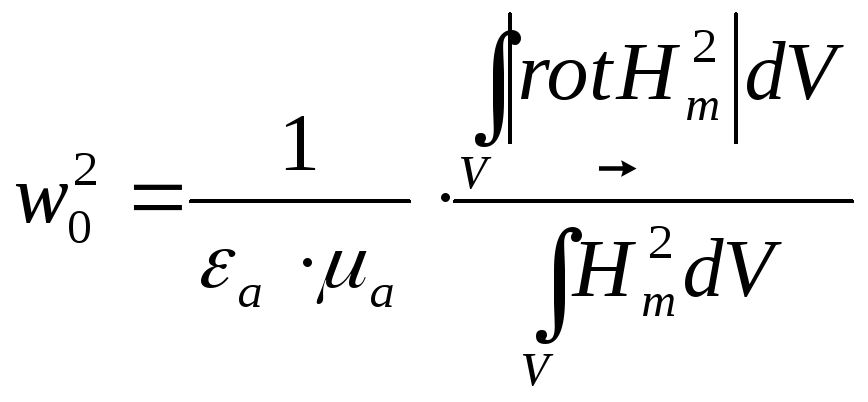 (4.52)
(4.52)
Формула (4.52) позволяет определить собственную резонансную частоту электромагнитных колебаний в объемном резонаторе. Из формулы (4.52) видно, что собственная резонансная частота зависит от размеров резонатора, свойств заполняющей резонатор среды и от структуры электромагнитного поля. Отсюда следует, что перестройку резонансной частоты можно выполнить с помощью изменения объема резонатора или заполняющей его среды. Изменить объем можно с помощью его укорочения или удлинения, т.е. за счет изменения длины. Также объем резонатора уменьшится, если внутри полости поместить металлическое тело. Иными словами, изменить объем резонатора можно двумя указанными выше способами. Это приводит к изменению резонансной частоты объемного резонатора.
Если в полость
резонатора поместить какой-либо
диэлектрик, имеющий определенное
значение ![]() ,
то резонансная частота также изменится.
,
то резонансная частота также изменится.
Собственную добротность резонатора можно определить, исходя из энергетического соотношения:
![]() (4.53)
(4.53)
где
![]() -энергия, запасенная
в резонаторе,
-энергия, запасенная
в резонаторе, ![]() - энергия, теряемая в резонаторе за один
период колебаний,
- энергия, теряемая в резонаторе за один
период колебаний,
![]() - собственная резонансная круговая
частота резонатора,
- собственная резонансная круговая
частота резонатора,![]() - мощность потерь в резонаторе.
- мощность потерь в резонаторе.
Получение высокой
добротности (т.е. большого значения)
является важным достоинством объемных
резонаторов. Так, резонаторы, изготовленные
из хорошо проводящего материала, имеют
добротность
![]() .
.
Резонаторы, выполненные на отрезках линий передачи электромагнитной энергии.
Объемные резонаторы СВЧ диапазона изготавливают на основе отрезков линий передачи электромагнитной энергии. Резонансные свойства будут проявляться на отрезке линии передачи, если потери энергии на концах этого отрезка достаточно малы и на длине отрезка происходит сложение многократно отраженных волн. На рис. 4.17. приведена схема резонатора на отрезке линии передачи.
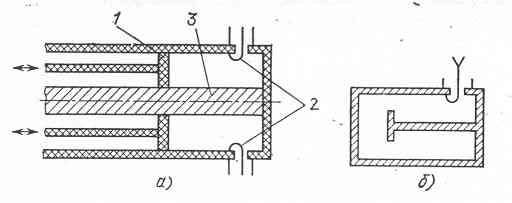
Рис. 4.17
Сложение многократно отраженных волн будет происходить в случае, если выполняется условие:
![]() (4.54)
(4.54)
где
![]() - число вариаций
поля вдоль отрезка линии, φ
– фаза коэффициента отражения от
нагруженного конца линии,
- число вариаций
поля вдоль отрезка линии, φ
– фаза коэффициента отражения от
нагруженного конца линии, ![]() - фазовая постоянная.
Формула (4.54) называется условием
резонанса.
- фазовая постоянная.
Формула (4.54) называется условием
резонанса.
Из формулы (4.54) выразим длину отрезка линии передачи, которая будет представлять собой длину резонатора:
![]() (4.55)
(4.55)
Рассмотрим основные типы резонаторов, выполненных на отрезках длинных линий. Заметим, что если число вариаций поля ρ>1 , то добротность резонатора уменьшается из-за потерь энергии, которые увеличиваются.
1 тип резонатора. Объемный резонатор представляет собой короткозамкнутый на обоих концах отрезок линии передачи. В этом случае φ=π. Тогда длина резонатора определяется формулой:
![]() (4.56)
(4.56)
где
![]() - число вариаций
поля,
- число вариаций
поля, ![]() -длина волны в
волноводе. Если
-длина волны в
волноводе. Если
![]() ,
то такой резонатор называетсяполуволновым.
,
то такой резонатор называетсяполуволновым.
2 тип резонатора. Объемный резонатор представляет собой отрезок линии передачи энергии, у которого один конец является короткозамкнутым, второй – разомкнутый. В этом случае у разомкнутого конца φ=0 и длина резонатора будет выражаться:
![]() (4.57)
(4.57)
Если
![]() ,то
,то![]() и резонатор называетсячетвертьволновым.
Четвертьволновые
резонаторы не изготавливаются из полых
волноводов, т.к. очень трудно выполнить
неизлучающий открытый конец.
и резонатор называетсячетвертьволновым.
Четвертьволновые
резонаторы не изготавливаются из полых
волноводов, т.к. очень трудно выполнить
неизлучающий открытый конец.
Резонаторы рассмотренных типов часто применяются в волномерах, предназначенных для измерения длины волны в трактах.
Мы рассмотрели условия создания резонаторов с помощью отрезков линий передачи электромагнитной энергии. Но линии передачи энергии бывают различных видов. Поэтому выберем отдельные конкретные виды линий передачи, на отрезках которых создаются резонаторы. Возьмем коаксиальную и волноводную линии передачи, и рассмотрим объемные резонаторы, созданные на их основе.
Коаксиальный резонатор.
На отрезке коаксиальной линии передачи выполнен соответственно коаксиальный объемный резонатор. Схемы конструкций различных типов коаксиальных резонаторов показаны на рис. 4.18.

Рис. 4.18
На рис. 4.18а показан полуволновый коаксиальный резонатор. На рис. 4.18б показан резонатор, который на разомкнутом конце имеет конструктивную емкость. Такая емкость позволяет уменьшать длину резонатора.
Поперечные размеры коаксиального резонатора выбираются также как и для самой коаксиальной линии, соблюдая соотношение:
![]() (4.58)
(4.58)
где
D
– диаметр наружного проводника, d
– диаметр внутреннего проводника
коаксиальной линии, ![]() -минимальная длина
волны.
-минимальная длина
волны.
От выбора значений
диаметров D
и d
зависят потери энергии в резонаторе.
Установлено, что наибольшая добротность
резонатора достигается при отношении
диаметров
![]() .
Если такое соотношение выполнено в
объемном резонаторе, то при резонансной
длине волны
.
Если такое соотношение выполнено в
объемном резонаторе, то при резонансной
длине волны![]() ненастроенный резонатор имеет добротность
ненастроенный резонатор имеет добротность![]() .
.
Резонаторы на основе прямоугольного и круглого волноводов.
Волноводные резонаторы представляют собой отрезки волноводных линий передачи энергии прямоугольного и круглого сечений, замкнутые с двух сторон поперечными металлическими стенками.
Для замкнутых объемных резонаторов выполняется общее условие резонанса:
![]() (4.59)
(4.59)
где
![]() -длина волны в
соответствующей линии передачи, которая,
как ранее было рассмотрено, определяется:
-длина волны в
соответствующей линии передачи, которая,
как ранее было рассмотрено, определяется:
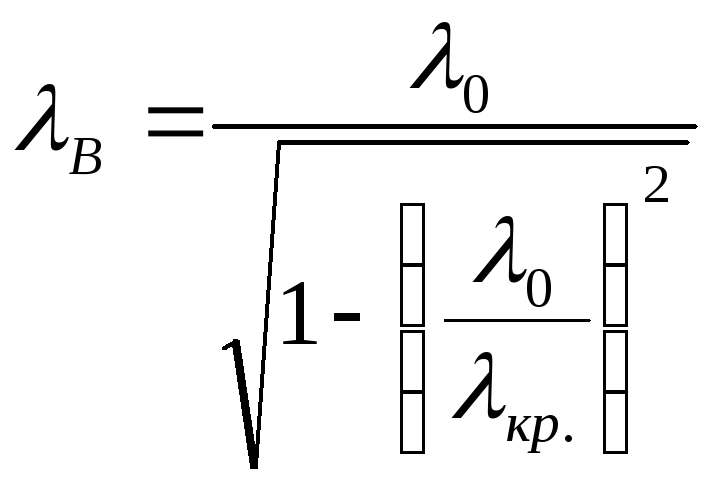 .
.
В случае, если длина резонатора l задана, то резонансные частоты такого резонатора определяются формулой:
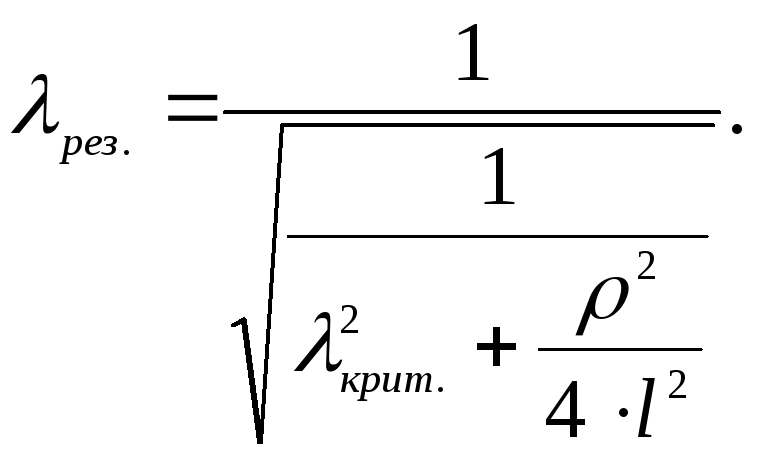 (4.60)
(4.60)
Если вариаций поля
вдоль оси нет, т.е.
ρ=0, то из
формулы (4.60) будем иметь
![]() .
.
На рис. 4.19 приведены схемы конструкций резонаторов, выполненных на волноводных линиях передачи круглого сечения.
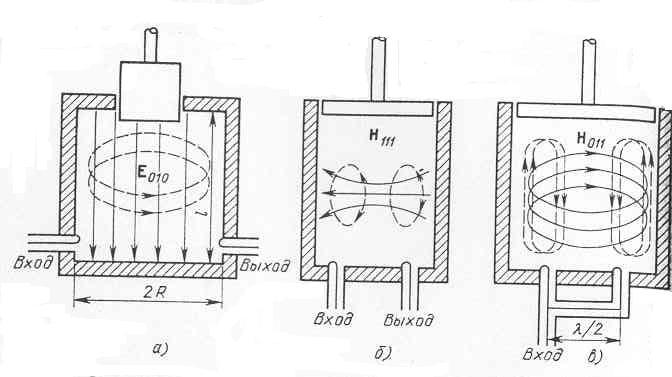
Рис. 4.19
На рис.4.19 приведены также структуры полей, возбужденных в резонаторах.
Помимо рассмотренных типов резонаторов, в СВЧ диапазоне также применяются диэлектрические и ферритовые резонаторы. Особый класс резонаторов составляют открытые резонаторы, применяемые в миллиметровом и субмиллиметровом диапазонах волн.
Элементы связи объемных резонаторов с внешними цепями.
Объемные резонаторы «связываются» с внешними цепями с помощью штыря, петли или отверстия. Элемент связи располагается в соответствии со структурой электромагнитного поля.
Штырь располагается вдоль силовых линий напряженности электрического поля.
Плоскость петли располагают перпендикулярно силовым линиям напряженности магнитного поля. Для размещения петли в корпусе резонатора прорезают щель, геометрические размеры которой должны быть существенно меньше длины волны.
Элемент связи в виде щели должен удовлетворять условиям: размеры щели не должны быть резонансными и на равной частоте щель должна иметь индуктивную проводимость. Резонатор должен располагаться так, чтобы структура поля в области щели и резонаторе совпадала, т.е. направления силовых линий напряженностей электромагнитного поля совпадали.
