Глава 1. Уравнения электромагнитного поля

1. Электромагнитное поле

Как известно, объективная реальность, в которой существует человек, называется материей. Материя существует в двух формах: в виде вещества и в виде поля. Предметом нашего изучения является электромагнитное поле.

Под электромагнитным полем понимают особую форму материи, с помощью которой осуществляется взаимодействие между заряженными частицами. Электромагнитное поле, как и вещество, имеет следующие свойства: обладает массой, импульсом, переносит энергию, испытывает воздействие гравитационных сил.

Электромагнитное поле представляет собой взаимосвязь двух полей: электрического и магнитного. Разделение единого электромагнитного поля на электрическую и магнитную составляющие имеет относительный характер. Источниками электромагнитного поля являются электрические заряды. Причем электрическое поле порождается электрическим зарядом, независимо от того находится он в покое или движется в выбранной системе координат. Магнитное поле порождается движущимся зарядом, т.е. электрическим током.

Относительный характер электромагнитного поля связан с выбором системы отсчета. Напомним, что система отсчета представляет собой совокупность тела отсчета, системы координат и часов, позволяющих отсчитывать время. Если в рассматриваемой системе отсчета прямолинейно движется электрический заряд с постоянной скоростью, то он порождает и электрическое и магнитное поле. Однако для наблюдателя, движущегося в направлении движения заряда с той же скоростью, заряд будет восприниматься неподвижным, и, следовательно, будет порождать только электрическое поле. Для наблюдателя это поле будет электростатическим, т.к. порождено неподвижным электрическим зарядом.

В природе, как известно, существуют положительные и отрицательные заряды. Элементарным положительным зарядом является заряд протона. Элементарным отрицательным – заряд электрона. Численные значения (модули) этих зарядов одинаковы, а знаки зарядов – разные. Численное значение элементарного заряда составляет q₀=1,610^-19 Кл.

Электрическое поле описывается вектором напряженности электрического поля и вектором индукции электрического поля. Магнитное поле описывается вектором напряженности магнитного поляи вектором индукции магнитного поля. Таким образом, в целом электромагнитное поле описывается четырьмя векторами,,,.

В международной системе измерений СИ единицами измерения указанных физических величин являются следующие: напряженность электрического поля (Е) – вольт на метр (); индукция электрического поля (Д) – кулон на квадратный метр (); напряженность магнитного поля (Н) – ампер на метр (); индукция магнитного поля (В) – тесла (Тл);

Электромагнитное поля распространяется в пространстве с течением времени с некоторой скоростью. В вакууме эта скорость соответствует скорости света с=310⁸ м/с. Поэтому векторы электромагнитного поля являются функциями пространственных координат и времени.

Источники электромагнитного поля (заряды) и векторные характеристики поля связаны между собой. Такая связь выражается с помощью соответствующих уравнений, которые представляют собой законы электродинамики. Приступим к более подробному рассмотрению этих законов. Отметим, что запись всех законов рассмотрим в международной системе измерений СИ.

2. Электрические заряды

Электродинамика изучает макроскопические заряженные тела. Минимальный заряд, существующий в природе в свободном состоянии, равен величине заряда электрона. Заряд реально заряженного тела кратен заряду электрона. Поэтому суммарный заряд тела определяется формулой

(1.1)

где q_i – элементарный заряд, входящий в состав тела.

Для описания заряда и его пространственного распределения введем соответствующие характеристики, к рассмотрению которых мы перейдем ниже.

Характеристики заряженного тела	Точечный заряд
	Объемная плотность заряда
	Поверхностная плотность заряда
	Линейная плотность заряда

Под точечным зарядом понимают заряд тела, размеры которого много меньше расстояния, на котором оно рассматривается.

Если заряд распределен по объему тела, то вводят понятие объемной плотности заряда. Объемная плотность заряда – это заряд, содержащийся в единице объема. Обозначается объемной плотностью заряда _е и определяется формулой

(1.2)

Объемную плотность заряда измеряют в кулонах на кубический метр ().

Очевидно, заряд элементарного объема определяется формулой

(1.3)

Полный заряд тела, имеющего объем V, равен сумме элементарных зарядов и определяется

, (1.4)

где q_T – полный заряд тела, _е - объемная плотность заряда, dV – элементарный объем.

В ряде случаев заряд расположен по поверхности тела, тогда удобно пользоваться поверхностной плотностью заряда . Поверхностная плотность заряда – это заряд, приходящийся на единичную площадь заряженного тела. Поверхностная плотность заряда определяется формулой

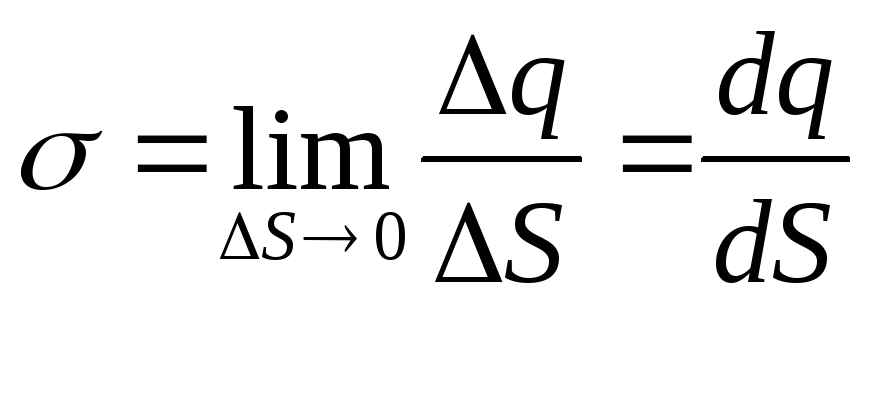
, (1.5)

где q – заряд, S – площадь поверхности. Единицей измерения поверхностной плотности заряда является кулон на квадратный метр ().

Очевидно, заряд элементарной поверхности находится из выражения

(1.6)

Полный заряд, находящийся на поверхности тела площадью S, определяется формулой

(1.7)

В случае расположения заряда вдоль нити вводят линейную плотность заряда. При таком идеализированном распределении заряда толщину нити принимают нулевой. Линейная плотность заряда – это заряд, приходящийся на единицу длины заряженной нити. Линейная плотность заряда определяется формулой

, (1.8)

где q – заряд, l – длина элемента нити. Единицей измерения линейной плотности заряда является кулон на метр ().

Исходя из определения, заряд элемента длины нити определяется

(1.9)

Полный заряд, приходящийся нить длинной L, определяется формулой

(1.10)

Отметим, в реальных условиях распределение заряда является объемным.

Точечные заряды взаимодействуют между собой по закону Кулона, который для вакуума имеет вид

, (1.11)

где - значения зарядов,r – расстояние между зарядами, - единичный радиус-вектор.

Понятие точечного заряда, поверхностной и линейной плотности заряда являются идеальными, использование которых существенно помогает упростить изучение содержания электродинамики.

3. Электрический ток

Проводящая среда характеризуется, как известно, наличием свободных заряженных частиц. Если в проводящей среде создано электрическое поле напряженностью, то заряды приходят в упорядоченное движение, т.к. электрическое поле действует силой на каждый заряд

(1.12)

Формула (1.12) показывает, что при положительном заряде q векторы иявляются сонаправленными. В случае отрицательного заряда векторыинаправлены в противоположные стороны.

Если на тело действует сила, то под ее действием тело приобретает ускорение, величина и направление которого определяется вторым законом Ньютона

, (1.13)

где - ускорение,- действующая сила,m – масса тела.

Таким образом, в проводящей среде свободные заряды под действием напряженности электрического поля приходят в упорядоченное движение, т.е. возникает электрический ток.

Электрический ток – это направленное движение зарядов. Для описания электрического тока вводят характеристики: сила тока и плотность тока.

Сила тока – это заряд, протекающий в единицу времени через поперечное сечение проводника. Обозначается сила тока I и определяется формулой

(1.14)

Сила тока I является скалярной величиной и измеряется в амперах

, (1.15)

т.е.

Для характеристики интенсивности движения зарядов и учета направления их движения ввели понятие объемной плотности электрического тока или часто говорят о плотности тока.

Плотность электрического тока - это векторная величина, направленная по напряженности электрического поля и численно равная отношению силы тока к размеру площади поверхности, через которую он протекает. Плотность электрического тока определяется формулой

, (1.16)

где - плотность тока,- единичный вектор,I – сила тока, S – площадь поверхности. Единицей измерения плотности тока является ампер на квадратный метр

(1.17)

В общем случае плотность тока неодинакова в разных точках пространства и является векторной функцией координат, т.е.

(1.18)

Характеристики электрического поля, т.е. сила тока и плотность тока, связаны между собой. Такая связь выражается формулой

, (1.19)

где I – сила тока, протекающая через поверхность S, - плотность тока,- направленная элементарная площадка площадьюdS.

Заметим, что ориентацию элементарной площадки dS учитывают с помощью единичного нормального вектора, проведенного к площадке (рис. 1.1).

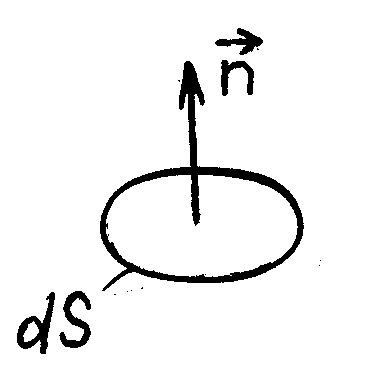
Рис. 1.1

Поэтому вектор определяется формулой

(1.20)

В формуле (1.19) произведение представляет собой поток вектора плотности тока, проходящего через указанную поверхность

(1.21)

Иными словами, электрический ток есть поток вектора плотности тока. Добавим, что электрический ток, обусловленный направленным движением реальных заряженных частиц, называется током проводимости.

По способности проводить электрический ток все среды можно классифицировать на проводники, диэлектрики и полупроводящие среды.

Проводники характеризуются способностью проводить электрический ток. Для характеристики проводящей среды ввели понятие удельной проводимости , которая зависит от физических свойств материала, температуры. Удельная проводимость измеряется в сименсах на метр ();

Диэлектрики не проводят электрический ток. Полупроводящая среда одновременно обладает свойствами и проводника, и диэлектрика.

Проводящей средой могут быть твердые тела, жидкости и газы. К проводникам в виде твердого тела относятся металлы, в которых свободными зарядами являются свободные электроны. К жидкостям, проводящим электрический ток, относятся кислоты, растворы солей, щелочи. В них свободными заряженными частицами являются ионы: положительные и отрицательные. В газах, при соответствующих условиях, проводят ток и ионы, и электроны.

Впроводящей среде для конкретной точки связь между векторами напряженности электрического поля и плотности тока выражается законом Ома в дифференциальной форме, в виде

, (1.22)

где - плотность тока, - удельная проводимость, - напряженность электрического поля.

Из формулы (1.22) видно, что вектор плотности электрического поля сонаправлен с вектором напряженности электрического поля, т.к. удельная проводимость вещества является положительной величиной.

4. Закон сохранения заряда

Многократно проведенными экспериментами установлено, что электрические заряды ни при каких условиях самопроизвольно не могут бесследно исчезать или зарождаться. Иными словами, экспериментально установлен закон сохранения заряда: в замкнутой системе полный заряд остается величиной постоянной, т.е.

(1.23)

Напомним, что система называется замкнутой, если тела, входящие в рассматриваемую систему, взаимодействуют только между собой, а с внешними телами не взаимодействуют.

Под полным зарядом подразумевают суммарный заряд всех заряженных тел, входящих в систему. На рисунке 1.2 показана замкнутая система, состоящая из четырех заряженных тел, обладающих соответственно зарядами q₁, q₂, q₃, q₄.

Рис. 1.2

Полный (суммарный) заряд системы равен

(1.24)

или такое сложение можно записать в виде

, (1.25)

где - суммарный заряд системы,q_i – заряд тела этой системы, i – индекс, указывающий номер тела, входящего в систему,  - знак суммы.

Закон сохранения заряда является фундаментальным физическим законом.

5. Закон Гаусса

Закон Гаусса устанавливает связь между электрическим зарядом и напряженностью электрического поля , которое он порождает.

Пусть внутри некоторого объема V, имеющего поверхность S, заключен суммарный электрический заряд q_ (рис. 1.3).

Рис. 1.3

Предварительно введем понятие потока вектора напряженности электрического поля в виде скалярного произведения двух векторов

(1.26)

Для пояснения содержания понятия потока вектора напряженности электрического поля , можно представить две параллельные плоскости, одна из которых заряжена положительно, т.е. имеет поверхностную плотность заряда +, вторая, соответственно, отрицательно -  (рис. 1.4).

Рис. 1.4

Пусть в пространстве между плоскостями расположена элементарная площадка , которая может занимать любую ориентацию. Очевидно, если вектор нормали, проведенный к площадке, сонаправлен (параллелен) вектору(), то площадкупересекает максимальное число линий напряженности электрического поля.

Если изменить ориентацию площадки, таким образом, что , т.е. угол между нормалью и направлением векторасоответствует 90, то при таком расположении силовые линии электрического поля не пересекают поверхности рассматриваемой площадки. В этом случае поток вектора напряженности электрического поля

, (1.27)

т.е. поток вектора равен нулю, силовые линии не пересекают поверхность.

Рис. 1.4 соответствует случаю максимального значения потока вектора напряженности электрического поля, т.к. векторы иявляются сонаправлеными.

Можно заключить, что понятие потока вектора показывает количество линий, пересекающих рассматриваемую поверхность.

Закон Гаусса математически записывается в виде

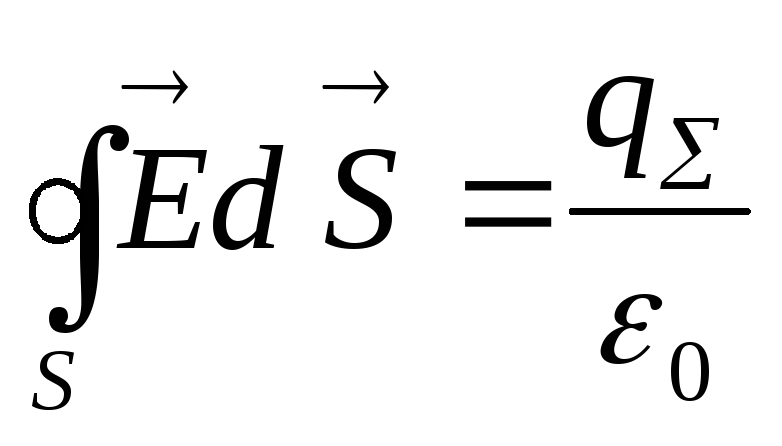, (1.28)

где - напряженность поля,- направленная площадка,- суммарный заряд, заключенный внутри поверхностиS, - диэлектрическая постоянная.

Скалярное произведение представляет собой поток вектора напряженности электрического поля, переносимый через площадку. Интегралозначает, что рассматриваем полный поток через всю замкнутую поверхность.

Закон Гаусса можно записать с помощью вектора индукции электрического поля. Для этого, уравнение (1.28) нужно несколько видоизменить, освободившись от знаменателя, т.е.

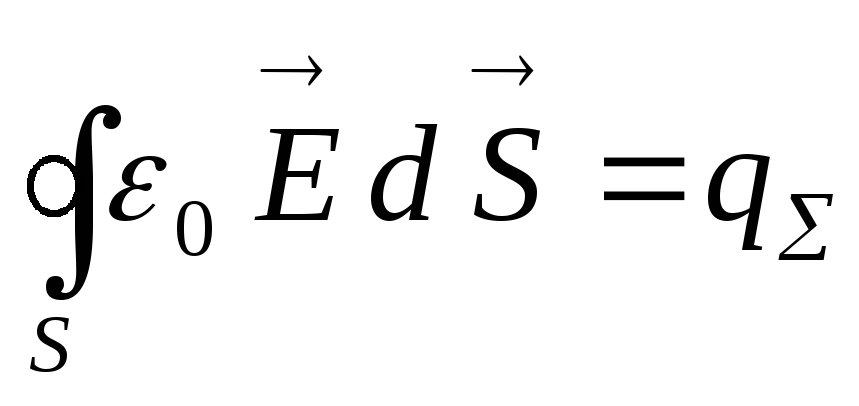, (1.29)

но произведение

, (1.30)

поэтому можно записать

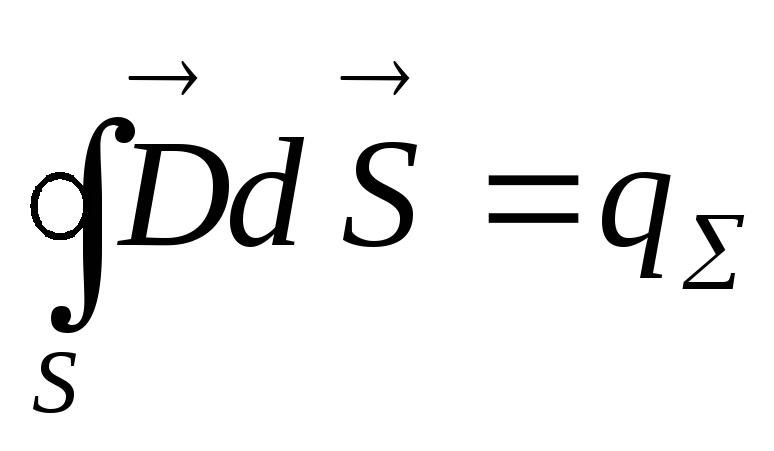(1.31)

Закон, записанный с помощью интеграла вдоль замкнутой поверхности, называется законом Гаусса в интегральной форме. Такая форма указывает на выполнение закона в целом, по всей поверхности рассматриваемого объема.

Заряды, как вы знаете, бывают положительные и отрицательные. Кроме того, нормаль к поверхности проводится внешняя (рис. 1.5). Для расчета потока вектора угол между вектороми нормальюв скалярном произведении отсчитывается от нормали к направлению вектора напряженности. Если суммарный заряд является положительным, то угол между внешней нормалью и напряженностью электрического поля будет меньше 90, > 0, значит> 0 (рис. 1.5а).

а) б) в)

Рис. 1.5

Если заряд отрицательный, то угол <0. В случае, если суммарный заряд заключенный в рассматриваемом объеме, равен нулю, то и поток векторасквозь замкнутую поверхность равен нулю (рис. 1.5в). В этом случае число силовых линий, входящих в объемV равно числу силовых линий , выходящих из этого объема.

Часто необходимо знать проявление закона в конкретных точках рассматриваемого пространства. Для этого заменим интеграл по поверхности через интеграл по объему на основе известного соотношения векторного анализа

_(1.32)

Таким образом, левую часть формулы (1.28) преобразовали, заменив интеграл по поверхности на интеграл по объему. Правую часть можно записать с помощью объемной плотности заряда_е. Суммарный заряд в формуле (1.31) выразим через объемную плотность заряда, т.е.

(1.33)

Тогда от интегральной формы записи закона можно перейти к дифференциальной

, (1.34)

Так как мы рассматриваем произвольный объем, то последнее равенство выполняется, если подынтегральные выражения равны между собой, т.е. можно записать

(1.35)

Формулу (1.35) можно также записать в виде

, (1.36)

т.е.

(1.37)

Формулы (1.35) и (1.37) называются законом Гаусса в дифференциальной форме.

Физически эти соотношения означают, что источниками электрического поля являются только электрические заряды. Иными словами, электрическое поле порождается электрическими зарядами.

Подчеркнем, что нормаль к элементу , выделенному по поверхности объема, проводится внешняя (рис. 1.6).

Рис. 1.6

Заряд в объеме может быть расположен произвольным образом. Кроме того, заряд внутри объема может изменяться с течением времени по произвольному закону.

Как известно, оператор дивергенции определяется как .

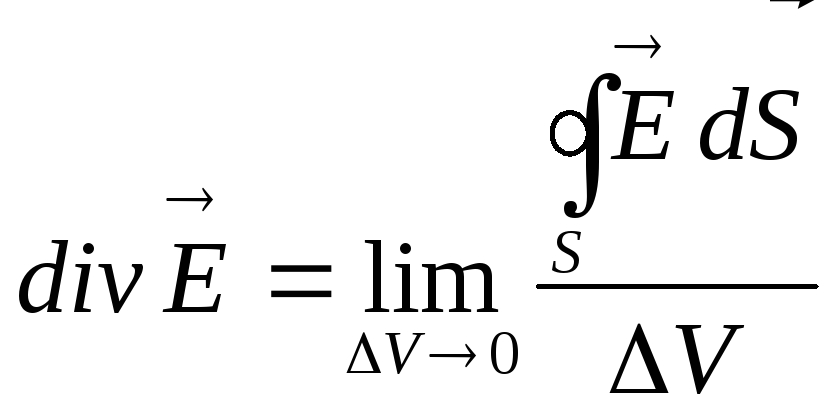Дивергенция является пределом отношения потока вектора через замкнутую поверхность S к величине объема V, ограниченной этой поверхностью. Дивергенция отлична от нуля, если в данной точке начинаются или заканчиваются силовые линии поля. Закон Гаусса указывает, что силовые линии поля могут начинаться или заканчиваться только в точках пространства, где существуют заряды. Если во всех точках рассматриваемой области заряд отсутствует, т.е. q = 0, то силовые линии поля пронизывают эту область насквозь, либо являются замкнутыми.

Таким образом, в точке пространства, в которой находится положительный заряд, т.е. q>0, то эта точка пространства с зарядом является «истоком» векторного электрического поля.

Если заряд отрицательный, т.е. q<0,(соответственно, _е<0), то и , такая точка пространства является «стоком» векторного электрического поля. На рис. 1.7 приведены соответствующие графические пояснения

Рис. 1.7

Закон Гаусса является фундаментальным, из него можно получить аналитическое выражение закона Кулона.

6. Закон неразрывности магнитных силовых линий

Магнитное поле, как установлено, порождается движущимся электрическим зарядом. Магнитное поле, описываемое векторами ,, можно представить в виде магнитных силовых линий. В свою очередь, магнитные силовые линии можно представить в виде воображаемых линий тока несжимаемой жидкости.

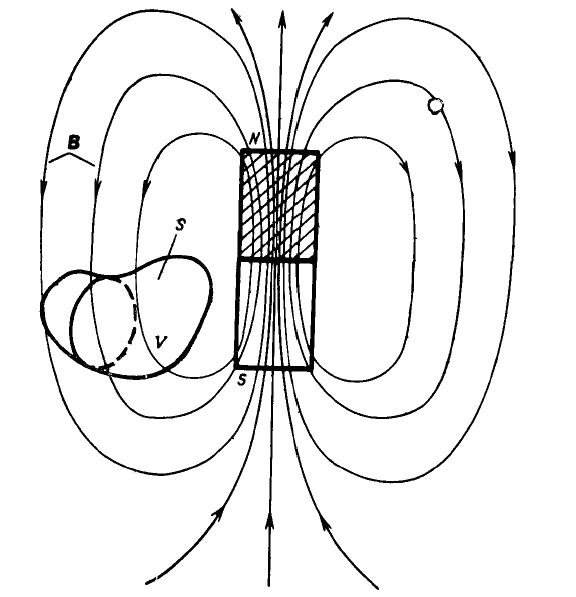
Для примера возьмем полосовой магнит, имеющий северный и южный магнитные полюсы. Картина силовых линий магнитного поля показана на рисунке 1.8.

Рис. 1.8. Полосовой магнит

Внутри области расположения силовых линий магнитной индукции расположим объем в виде цилиндра, хотя в общем случае можно взять объем произвольной формы. Т.к. силовые линии магнитного поля являются замкнутыми, то ясно, что поток втекающей жидкости равен потоку вытекающей жидкости из этого объема. Поэтому можно записать равенство нулю потока вектора магнитной индукции в виде:

(1.38)

Если выполнить операции, аналогичные приведенным в пункте 1.5, то можно получить закон неразрывности магнитных силовых линий в дифференциальной форме

(1.39)

Другими словами, векторное магнитное поле не имеет источников, т.е. в природе не существует реальных магнитных зарядов.

7. Закон полного тока

Как известно, если по проводнику протекает электрический ток, то в пространстве возникает магнитное поле. Существование магнитного поля вокруг всякого проводника с током доказал в начале XIX века Х.Эрстед. Закон полного тока выражает связь между электрическим током и порождаемым им магнитным полем.

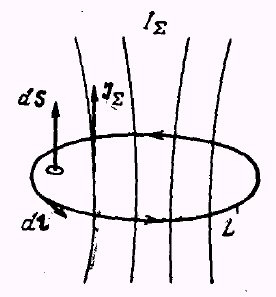
Допустим, что имеется несколько проводников, по каждому из которых протекает соответствующий электрический ток (рис. 1.9). Силой I₁, I₂, I₃,… I_N. Возьмем произвольный контур и охватим им проводники с током. Контур ограничивает поверхность S. Выберем направление обхода контура. Для этого предварительно на воображаемой площади S произвольно выберем элементарную площадку , к которой восстановим единичный нормальный вектор. Направление обхода контура выберем так, чтобы оно совпадало с вращательным движением правовинтового буравчика при условии, что поступательное движение буравчика совпадает с направлением вектора нормали, восстановленного к площадке(рис. 1.9).

Рис. 1.9

Добавим, что рассматриваемая совокупность токов имеет дискретный характер, т.к. состоит из отдельных проводников, по которым текут токи. Электрический ток может иметь также непрерывный характер и представлять собой, например, направленный поток электронов.

Закон полного тока выражает связь между силой протекающего суммарного тока через замкнутый контур длиной L и напряженностью магнитного поля, которое порождается этим током.

В интегральной форме закон полного тока выражается формулой

, (1.40)где - вектор напряженности магнитного поля,- направленный элементарный линейный участок, взятый вдоль контура,- суммарная сила тока. Интеграл по замкнутому контуру произведенияназывается циркуляцией вектора.

Отметим, если контур охватывает непрерывный пространственный поток движущихся заряженных частиц с плотностью электрического тока , то сила полного тока, пронизывающего контур, определяется выражением

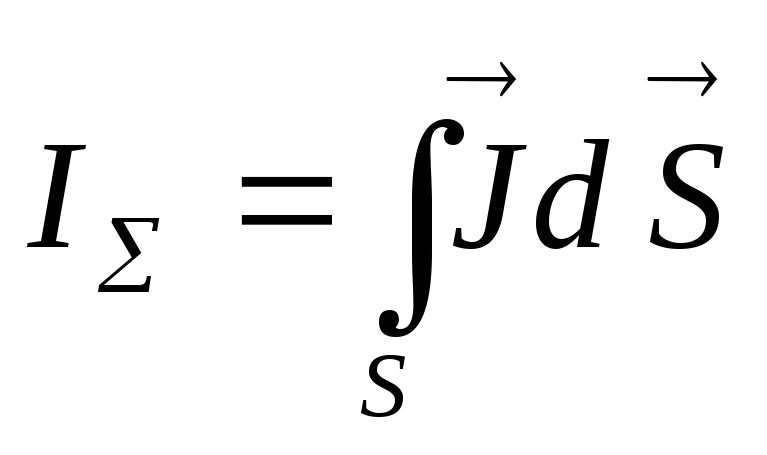(1.41)

Произведение представляет поток вектора плотности тока, пронизывающего поверхностьdS.

Часто на практике для решения задач следует применять дифференциальную форму закона полного тока. Для записи закона полного тока в дифференциальной форме необходимо интеграл по замкнутому контуру L (циркуляцию вектора ) выразить через интеграл по площадиS, которую охватывает замкнутый контур. Для этого воспользуемся теоремой Стокса, которая в векторном анализе выражается соотношением

(1.42)

Для нашего случая теорема Стокса запишется в виде

(1.43)

Тогда формулу (1.40) можно преобразовать на основе выражения (1.42) и (1.43), вследствие чего получим соотношение

(1.44)

Т.к. контур L взят произвольным образом, то интегралы в левой и правой части равенства будут равны, если равны подынтегральные выражения. В результате можно записать

(1.45)

Формула (1.45) выражает закон полного тока в дифференциальной форме.

Рассмотрим простой пример расчета напряженности магнитного поля, созданного протекающим по прямолинейному проводнику постоянным электрическим током. на рисунке 1.10 показан отрезок прямолинейного проводника, по которому протекает электрический ток силой I.

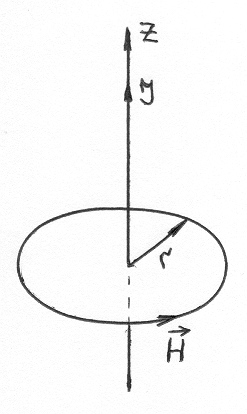
Рис. 1.10

Постоянный электрический ток силой I порождает постоянное магнитное поле, характеризующееся напряженностью . Силовые линии напряженности магнитного поляпредставляют замкнутые силовые линии. Направление силовых линийдля прямолинейного проводника с током определим с помощью правила буравчика. Для этого вращаем правовинтовой буравчик в правую сторону таким образом, чтобы его поступательное движение совпадало с направлением движения электрического тока, тогда направление вращательного движения укажет направление силовой линии.

Закон полного тока в интегральной форме имеет вид .Cиловая линия представляет собой окружность с центром, лежащем на оси проводника с током. Обозначим радиус окружности черезr. Учтем, что во всех точках окружности (контура) напряженность поля имеет одно и то же значение, т.к. все радиальные направления равноправны. Поэтому циркуляцию вектораможно записать в виде

(1.46)

На основании закона полного тока циркуляция вектора равна протекающему току, т.е. имеем, отсюда можно выразить напряженность магнитного поля

(1.47)

Таким образом, получили формулу для определения значения напряженности магнитного поля, созданного прямолинейным проводником, по которому протекает постоянный электрический ток силой I. Направление силовых линий определяется, как сказано выше, с помощью правила буравчика.

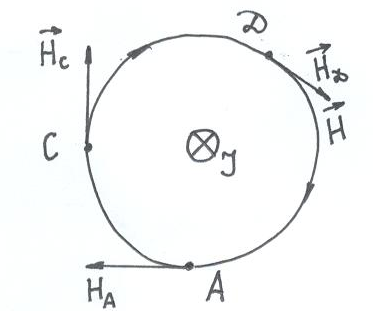
Направление вектора для любой точки пространства определяется с помощью касательной, проведенной в данной точке пространства к силовой линии. На рис. 1.11 показано сечение проводника с силой тока I, текущего от нас (направление тока показано крестиком) и силовая линия , представляющая собой окружность с радиусомr.

r

Рис. 1.11

В точках A, C, D показано направление вектора . Значение напряженности магнитного поля является одинаковым, поэтому длина всех векторов,,также одинакова, а их направления в конкретных рассматриваемых токах будут разными, т.к. направлены по касательным.

8. Ток смещения

Как известно, протекание электрического тока по проводнику, вызывает в пространстве появление магнитного поля. Но установлено, что не только ток проводимости порождает магнитное поле. Иными словами, не только ток проводимости является источником магнитного поля.

Магнитное поле порождается также током смещения, который в принципе имеет совершенно иную природу, чем ток проводимости. Напомним, что электрический ток проводимости обусловлен направленным движением реальных заряженных частиц, движущихся под воздействием электрического поля.

Для выяснения понятия «ток смещения» рассмотрим электрическую цепь, содержащую плоский конденсатор (рис. 1.12). Пусть одна обкладка конденсатора имеет в данный момент времени положительный заряд +q, вторая соответственно, - отрицательный. Внутри конденсатора между обкладками создается обкладок электрическое поле напряженностью .

Рис. 1.12

Применим к одной из обкладок закон Гаусса. Для этого мысленно окружим положительно заряженную обкладку замкнутой поверхностью S. Закон Гаусса имеет вид

Тогда величина заряда, находящегося внутри замкнутой поверхности (положительной обкладки), можно выразить

Так как через замкнутую цепь, содержащую конденсатор, течет переменный ток, то можно выразить величину этого тока:

Величина имеет размерность плотности тока, которая и была названа плотностью тока смещения. Итак, плотность тока смещения определяется формулой

, (1.48)

тогда сила тока смещения определяется выражением

(1.49)

Таким образом, как только в пространстве (среде) возникает изменяющееся с течением времени электрическое поле, то такое изменение называется плотностью тока смещения и оно порождает магнитное поле. Подчеркнем, что хотя природа тока проводимости, обусловленная направленным движением заряженных частиц, и тока смещения, обусловленная изменением вектора напряженности электрического поля, различна, эти токи играют роль эквивалентных источников магнитного поля. Иными словами, ток проводимости и ток смещения порождают в пространстве магнитное поле, другими словами, являются источниками магнитного поля.

Вышеизложенное указывает, что если в пространстве имеется изменяющееся электрическое поле, то возникает магнитное поле, которое обнаруживается экспериментально. Рассмотрим пример, показанный на рис. 1.12. Пусть в пространстве имеется электрическое поле, которое в одном случае возрастает (а), в другом – убывает с течением времени (б). Электрическое поле задано с помощью вектора электрического смещения , изменение электрического поля с течением времени соответствует наличию производной, которая, в свою очередь, определяет плотность тока смещения, так как. На рис. 1.12а графически показан случай усиления электрического поля с течением времени, на рис. 1.12б – ослабления поля.

Рис. 1.12

Плотность тока смещения порождает магнитное поле, которое изображается с помощью замкнутых силовых линий. Направление обхода замкнутой силовой линии определяется правовинтовым буравчиком, т. е. буравчик вращается в правую сторону, или почасовой стрелке. Поступательное движение буравчика совпадает с направлением вектора плотности тока смещения , а направление вращательного движения правовинтового буравчика укажет искомое направление обхода. В первом случае (рис. 1.12а) направления векторовисовпадают, во втором – направления векторовиявляются противоположными.

9. Закон электромагнитной индукции

В истории человечества открытие закона электромагнитной индукции сыграло важную роль, так как именно этот закон дал толчок развитию всей электротехники, позволил создать способы получения электромагнитной энергии, разработать различные типы двигателей и многочисленных устройств. В основе всей электротехники лежит открытие М. Фарадея, который в 1831 году обнаружил появление электрического тока в замкнутом контуре, находящемся в изменяющемся магнитном потоке.

В чем заключается сущность закона электромагнитной индукции? Предварительно напомним сущность понятия потока электромагнитной индукции. Поток вектора электромагнитной индукции в соответствии с определением потока (любого) вектора записывается в виде , (1.50)

где - поток вектора,- индукция магнитного поля,- направленная площадка, ограниченная контуром,- нормаль, проведенная к площадке,- угол между направлением вектора индукции магнитного поляи нормалью.

Магнитный поток измеряется в веберах .

Из формулы (1.50) видно, что поток вектора магнитной индукции можно изменить с течением времени тремя способами, связанными с изменением:

• модуля вектора магнитной индукции , то есть изменяя численное значение индукции поля;

• площади контура;

• угла между направлением вектора 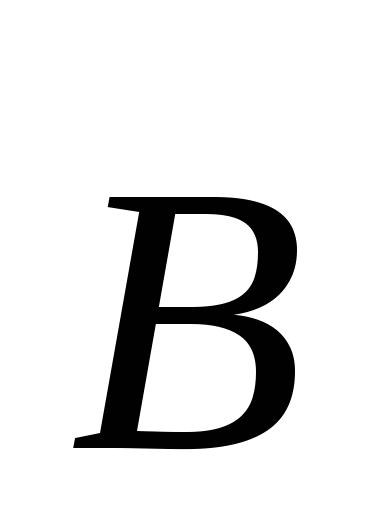и нормалью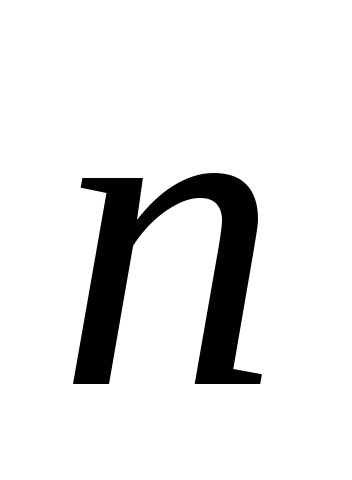, восстановленной к площадке, т. е. поворачивая произвольным образом контурв магнитном поле.

Все рассмотренные способы приводят к изменению магнитного потока .

Фундаментальный закон электромагнитной индукции устанавливает связь между изменяющимся магнитным потоком и возникающим электрическим полем. Пусть имеется изменяющееся магнитное поле, причем его изменение связано непосредственно с изменением вектора магнитной индукции . Соответственно, имеется изменяющийся магнитный поток. В таком поле рассмотрим произвольный замкнутый контур длиной(рис. 1.13).

Рис. 1.13

В курсе общей физики закон электромагнитной индукции записывается в виде:

, (1.51)

где - ЭДС индукции,- изменение потока магнитной индукции,- время, в течение которого произошло изменение магнитного потока. Знак минус выражает правило Ленца, указывающее на противодействующий характер магнитного поля, возникающего вследствие индукции по отношению к внешнему магнитному полю.

В интегральной форме закон электромагнитной индукции имеет вид

, (1.52)

где - напряженность электрического поля,- направленный элемент длины проводника,- магнитная индукция,- площадь, ограниченная контуром длиной.

Циркуляция вектора напряженности электрического поля, т. е. выражает собой электродвижущую силу (ЭДС), возникающую в контуре под действием которой появляется электрический ток. Отметим, что контур может быть как мысленно рассматриваемый, так и реально взятый в виде замкнутого проводника.

Для получения закона электромагнитной индукции в дифференциальной форме необходимо воспользоваться теоремой Стокса, в результате интеграл по длине контура преобразуется в интеграл по площади.

Итак, запишем

.

Закон электромагнитной индукции можно записать в виде

Так как взят произвольный контур, то интегралы будут равны, если подынтегральные выражения равны, т. е.

(1.53)

Формула (1.18) выражает дифференциальную форму закона электромагнитной индукции, которая указывает связь между электрическим и магнитным полем в каждой точке пространства.

Оператор содержит только пространственные производные, в правой части формулы (1.53) членвыражает производную по времени. Отсюда видно, что характер изменения напряженности магнитного поляс течением времени определяет характер изменения напряженности электрического поляв пространстве.

Таким образом, закон электромагнитной индукции показывает, что изменение магнитного поля в пространстве с течением времени приводит к возникновению электрического поля.

Рассмотрим несколько примеров.

Пример 1. Пусть электрическое поле отсутствует, т.е. напряженность электрического поля . Тогдаи. Равенство производной нулю означает, что магнитная индукцияможет быть только постоянной величиной, т. е.. Полученные выражения показывают, что в отсутствии электрического поля, магнитное поле может быть только постоянным.

Пример 2. Пусть имеется изменяющееся магнитное поле, это означает что и, т. е. существует производная по времени. Тогда согласно закону электромагнитной индукции, т.е.. Отсюда следует, что.

Таким образом, изменение во времени магнитного поля приводит к возникновению электрического поля.

Пример 3. Определим связь между направлениями силовых линий электрического и магнитного поля. Пусть имеется изменяющееся магнитное поле, в первом случае (рис. 1.14а) поле возрастает, во втором (рис. 1.14б) – убывает.

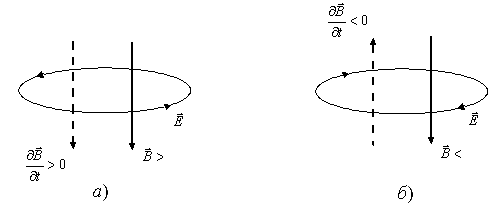
Рис. 1.14

Поместим замкнутый контур в такое изменяющееся магнитное поле. Так как магнитный поток, пересекающий контур, изменяется, то возникает электрическое поле напряженностью , в контуре будет наводиться ЭДС, и возникнет электрический ток. Причем ток будет иметь такое направление, что порождаемое им магнитное поле будет противодействовать первоначальному внешнему магнитному полю. В результате, в случае (рис. 1.14а) векторыисонаправлены, силовые линии напряженности электрического поля имеют направление против часовой стрелки; в случае рис. 1.14б векторыинаправлены в противоположные стороны, силовые линии напряженности электрического поля направлены по часовой стрелке

Подчеркнем, что наличие проводящего контура не является обязательным. Ток, индуцированный в проводящем контуре, возникает в результате силового воздействия напряженности электрического поля на свободные заряды, существующие в проводнике. Возникновение самого электрического поля не связано с наличием реального контура. Если отсутствует контур, то электрическое поле возникает в вакууме, а также в любой другой среде. Именно такое положение утверждает закон электромагнитной индукции.

Электрическое поле, порождаемое переменным магнитным полем, является вихревым. Силовые линии такого поля являются замкнутыми.

Уравнения Максвелла, выражающие закон электромагнитной индукции в интегральной и дифференциальной формах содержат характеристики магнитного и электрического полей. Иными словами, уравнения Максвелла никак не связаны с материальным контуром, они в чистом виде содержат поля и носят обобщенный характер. Можно сказать, что уравнения Максвелла являются полевыми уравнениями и связывают поле в данном месте пространства в конкретный момент времени. Переменное магнитное поле создает вокруг себя вихревое электрическое поле.

9. Материальные уравнения электромагнитного поля для вакуума

Рассмотренные выше четыре уравнения Максвелла образуют фундаментальную систему уравнений электродинамики. Такая система уравнений справедлива для любой среды, в которой происходит распространение полей. Однако, чтобы система уравнений была полной и однозначно определяла поле в любой точке среды, необходимо добавить уравнения, учитывающие свойства самой среды, которые проявляются в характере связи между характеристиками поля, то есть между и,и. Уравнения, устанавливающие связь между указанными характеристиками поля с учетом свойств среды, называются материальными уравнениями.

Среда, в которой происходят электрические и магнитные явления, характеризуется диэлектрической проницаемостью , магнитной проницаемостьюи удельной проводимостью.

В вакууме материальные уравнения имеют вид:

,

, (1.54) где - электрическая постоянная,- магнитная постоянная.

С точки зрения способности проводить электрический ток все среды делят на проводники, диэлектрики, и полупроводники.

Проводники – это вещества, способные проводить электрический ток, обладают удельной проводимостью (сименс на метр).

Диэлектрики – это вещества, не способные проводить электрический ток. Диэлектрики характеризуются удельной проводимостью .

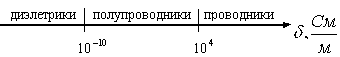
Рис. 1.15

Полупроводники – это вещества, которые обладают одновременно и свойствами проводника, и свойствами диэлектрика. Для полупроводников удельная проводимость изменяется в пределах .

На рис. 1.15 показано разделение веществ по значению удельной проводимости.

Во многих задачах электродинамики удобно реальные проводники и диэлектрики заменить идеальными проводниками и диэлектриками. В этом случае, для идеального проводника принимаем , идеального диэлектрика.

Поведение проводников в электрическом поле мы рассмотрели выше, где выяснили, что под действием внешнего электрического поля в проводнике наводится ток проводимости в соответствие с дифференциальным законом Ома, т.е. . Влияние магнитного поля мы пренебрегаем.

9. Поведение диэлектриков в электрическом поле

Представляет интерес поведение диэлектрика, помещенного во внешнее электрическое поле. Предварительно, напомним, что все вещества состоят из молекул. Молекулы состоят из атомов. Атом состоит из положительно заряженного ядра и электронной оболочки. Атом является нейтральной структурой, т.е. его заряд равен нулю, т.к. число электронов равно числу протонов ядра.

Также напомним, что с точки зрения строения молекул все диэлектрики можно разделить на два класса: полярные и неполярные.

Полярные диэлектрики – это диэлектрики, состоящие из полярных молекул, у которых центры тяжести положительных и отрицательных зарядов не совпадает между собой. У полярных диэлектриков можно выделить два полюса: положительный и отрицательный. Такая система эквивалентна диполю. Электрическим диполем – называется система двух одинаковых по величине, но разных по знаку зарядов и, расположенных на некотором расстоянии. Такой диполь схематично показан на рис. 1.15.

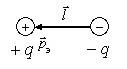
Рис. 1.16

Электрический диполь характеризуется дипольным моментом

, (1.55)

где - заряд,- расстояние между положительным и отрицательным зарядами. Дипольный момент направлен от отрицательного к положительному заряду. Измеряется дипольный момент в Кулонах на метр ().

Таким образом, дипольным моментом изначально обладают полярные диэлектрики. Отметим, что к полярным диэлектрикам относятся вода, спирт, некоторые твердые вещества (полихлорвинил).

Неполярные диэлектрики – это диэлектрики, состоящие из молекул, у которых центр тяжести положительного и отрицательного заряда совпадают. Неполярные диэлектрики не обладают собственным дипольным моментом. К неполярным диэлектрикам относятся большинство газов, многие твердые диэлектрики (кварц, стекло, полиэтилен). Принадлежность молекулы к тому или другому типу диэлектрика определяется ее внутренней структурой.

Рассмотрим поведение диэлектриков, помещенных в электрическое поле. Первоначально разберем сущность происходящего физического явления для полярных молекул. Если внешнее электрическое поле отсутствует, то молекулы в виде электрических диполей ориентированны хаотично в пространстве, как показано на рис. 1.17а.

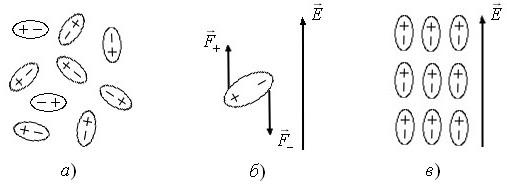
Рис. 1.17

Если поместить диэлектрик в электрическое поле напряженностью , то на каждый заряд диполя со стороны поля будет действовать кулоновская сила (рис. 1.17б). В результате действия сил диполь начинает разворачиваться так, чтобы собственный дипольный момент приобрел преимущественную ориентацию относительно поля(рис. 1.17в).

Пусть в единице объема содержится диполей (молекул), общий вектор поляризацииопределяется формулой

, (1.56)

где - концентрация дипольных молекул,- элементарный дипольный момент,- суммарный дипольный момент.

Остановимся на поведении неполярного диэлектрика в электрическом поле. В отсутствии электрического поля центры тяжести положительного и отрицательного зарядов совпадают, так как заряды имеют единый центр тяжести. Схематичное изображение неполярной молекулы показано на рис. 1.18а.

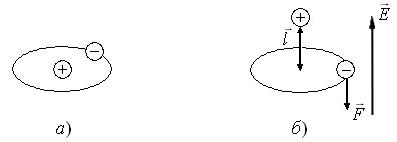
Рис. 1.18

При внесении неполярной молекулы в электрическое поле на каждый заряд со стороны электрического поля действует кулоновская сила. Но силой действия на положительный заряд (ядро) следует пренебречь, так как масса протона (положительного заряда) больше массы электрона почти в 2000 раз. Сила, действующая со стороны электрического поля на электрон, приложена к электрону и направлена в противоположную сторону относительно напряженности электрического поля (). В результате действия такой силы орбита электрона смещается в рассматриваемом случае (рис. 1.18б) вниз на расстояние. В результате смещения орбиты электрона центры тяжести положительного и отрицательного зарядов не будут совпадать. Центр тяжести отрицательного заряда сместится вниз под действием внешнего поля, в результате чего в молекуле индуцирован (навелся) дипольный момент. Как только электрическое поле исчезнет, то электрон вернется на свою прежнюю орбиту и наведенный дипольный момент исчезнет (, так как).

На основе рассмотренного выше материала дадим определение понятию “поляризация диэлектриков”. Поляризация диэлектриков – это процесс возникновения в диэлектриках состояния, характеризующегося наличием дипольного момента в любом элементе объема под действием внешнего электрического поля.

Количественно явление поляризации диэлектриков описывается вектором поляризации(суммарный дипольный момент) или просто поляризацией. Для большинства веществ между вектором поляризациии напряженностью внешнего электрического полясуществует прямо пропорциональная зависимость, которая записывается в виде:

, (1.57)

где - диэлектрическая восприимчивость вещества.

В электродинамике для описания явлений, происходящих в диэлектрике, вводят вектор электрической индукции или вектор электрического смещения

(1.58)

подставим формулу (1.57) в (1.58), получим

(1.59)

Выражение в скобках формулы (1.59) представляет абсолютную диэлектрическую проницаемость

(1.60)

Вектор индукции электрического поля можно записать в виде .

На практике часто используют относительную диэлектрическую проницаемость, которая определяется выражением

(1.61)

В большинстве случаев нет необходимости в детальном рассмотрении процесса поляризации диэлектриков. В таблице 1.1 приведены значения относительной диэлектрической проницаемости для некоторых диэлектриков.

Таблица 1.1 Значения относительной диэлектрической проницаемости

Материал	Относительная диэлектрическая проницаемость,
Фторопласт Полиэтилен Полистирол Плавленый кварц	2,08 2,25 2,56 3,8

Из-за поляризации внутри диэлектрика создается поле напряженностью, направление которого противоположно направлению внешнего электрического поля. Рассмотрим пример.

Пример 4. Электрическое поле напряженностью создано плоским конденсатором (рис. 1.19).

Рис. 1.19

В пространство между пластинами конденсатора помещен диэлектрик. В результате поляризации на боковых поверхностях диэлектрика индуцируется заряд, с одной стороны – отрицательный, с другой – положительный. За счет наведенного связанного заряда внутри диэлектрика создается поле напряженностью . Таким образом, внешнее поленаправлено слева направо, а индуцированное полеза счет поляризации направленно в противоположную сторону. Результирующее поле внутри диэлектрика будет меньше напряженности внешнего электрического поля и определяется формулой:

(1.62)

Существуют диэлектрики, которые в отсутствие внешнего электрического поля способны самопроизвольно образовывать поляризованные области (домены). Такие диэлектрики называются сегнетоэлектриками или ферроэлектриками. Сегнетоэлектрики имеют относительную диэлектрическую проницаемость , которая может составлять несколько тысяч единиц. К сегнетоэлектрикам относится титанат бария.

9. Поляризационные и сторонние токи

В процессе поляризации диэлектриков происходит направленное движение заряженных частиц под действием внешнего электрического поля напряженностью . Такое направленное движение зарядов в диэлектрике представляет собойполяризационный ток. Отметим, что принципиальной разницы между поляризационным током и током проводимости не существует.

Поляризационный ток характеризуется плотностью поляризационного тока, которая определяется формулой

(1.63)

Ранее мы выяснили физический смысл плотности токов проводимости и смещения. Поэтому теперь мы можем более подробно записать формулу закона полного тока , где- суммарная плотность тока и представляет собой сумму всех существующих типов плотности тока. Таким образом, можно записать

(1.64)

Следует также учесть плотность стороннего тока , который возникает вследствие действия сторонних электродвижущих сил. Рассмотрим действие сторонних электродвижущих сил более подробно.

Ток проводимости обусловлен действием внешнего электрического поля на свободные заряженные частицы с силой . Таким образом, сила, действующая со стороны поля на частицу, совершает работу по ее перемещению на расстояние, т.е. работа, совершаемая электрическим полем, определяется как. При этом происходит затрата энергии со стороны электрического поля. Для пополнения энергии поля необходимо наличие сил, которые не имеют никакого отношения к электромагнитному полю и перемещают заряды против сил поля. Такие силы называютсясторонними электродвижущими силами. Работа сторонних сил на участке отрицательна, т. е. сторонние силы увеличивают энергию электромагнитного поля. Роль сторонних сил могут играть любые силы неэлектрической природы. Ими могут быть механические силы, силы химического взаимодействия и другие.

Учитывая плотность тока сторонних электродвижущих сил, закон полного тока в дифференциальной форме, следует записать

Учитывая, что , таким образом, окончательно уравнение Максвелла запишется в виде

(1.65)

Это уравнение получило название первое уравнение Максвелла.

9. Поведение магнетиков в магнитном поле

Рассмотрим поведение веществ, помещенных во внешнее магнитное поле с индукцией . В этом случае мы рассматриваем не сам заряд, а именнодвижущийся заряд. Таким движущимся зарядом является движущийся по круговой орбите электрон. Как известно, направленное движение заряда представляет собой электрический ток. Поэтому движение электрона по орбите следует рассматривать как электрический ток силой . Введем понятиеэлементарного магнитного диполя – это движущийся по орбите электрон, обладающий орбитальным магнитным моментом. Элементарный электрический ток характеризуется магнитным моментом , который определяется формулой

, (1.66)

где - магнитный момент,- сила тока,- вектор элементарной площадки. На рис. 1.20 показано графическое изображение элементарного тока с вектором магнитного момента.

Рис. 1.20

Магнетиками называются вещества, способные намагничиваться. Если магнетик помещен в пространство, в котором отсутствует магнитное поле, то магнитные моменты имеют хаотичную ориентацию, как показано на рис. 1.21а. Если магнетик помещен в магнитное поле с индукцией , то под действием этого поля элементарные магнитные моментыориентируются в пространстве таким образом, чтобы вектор магнитного момента был сонаправлен с вектором магнитной индукции, т.е.. Упорядоченная ориентация молекулярных токов также показана на рис. 1.21б.

Рис. 1.21

Такой процесс называется намагничиванием. Иными словами, намагничивание – это процесс частичной ориентации молекул магнетика во внешнем магнитном поле.

Намагниченность вещества характеризуется вектором намагниченности , который определяется формулой

, (1.67)

где - вектор намагниченности вещества,- концентрация молекул,- элементарный магнитный момент.

Экспериментально установлено, что у большинства веществ при не слишком больших магнитных полях существует связь между вектором намагниченности и напряженностью внешнего действующего магнитного поля, которая выражается линейной зависимостью и определяется формулой

, (1.68)

где - намагниченность,- напряженность поля,- магнитная восприимчивость вещества.

Установлено, что магнитные свойства вещества можно описать, если вектор магнитной индукции представить в виде:

, (1.69)

где - индукция,- магнитная постоянная,- напряженность магнитного поля,- намагниченность вещества. Учитывая формулу (1.68), можно формулу (1.69) записать в виде

. (1.70)

Введем обозначение

, (1.71)

где величина называется абсолютной магнитной проницаемостью вещества.

Уравнение (1.70) с учетом формулы (1.71) принимает наиболее простой вид

, (1.72)

где - абсолютная магнитная проницаемость вещества.

Если среда является вакуумом, то намагниченностьи связь междуипринимает наиболее простой вид

(1.73)

Для практических расчетов часто используют относительную магнитную проницаемость, которая определяется отношением

(1.74)

Все магнетики (вещества) в зависимости от значения относительной магнитной проницаемости делят на 3 класса:

• диамагнетики, если ;

• парамагнетики, если ;

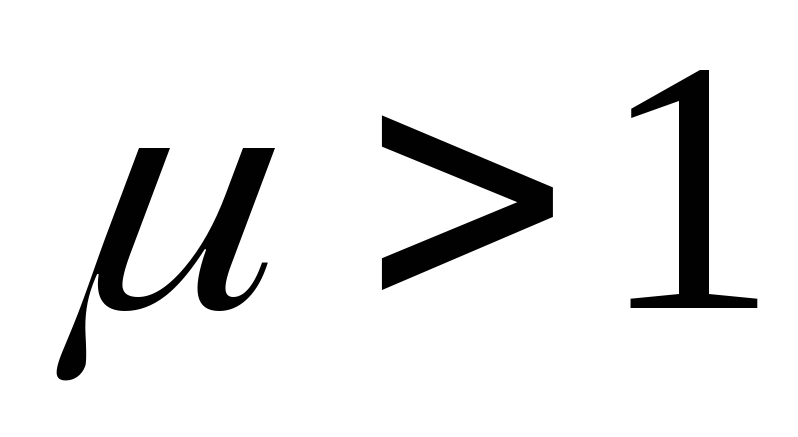• ферромагнетики, если .

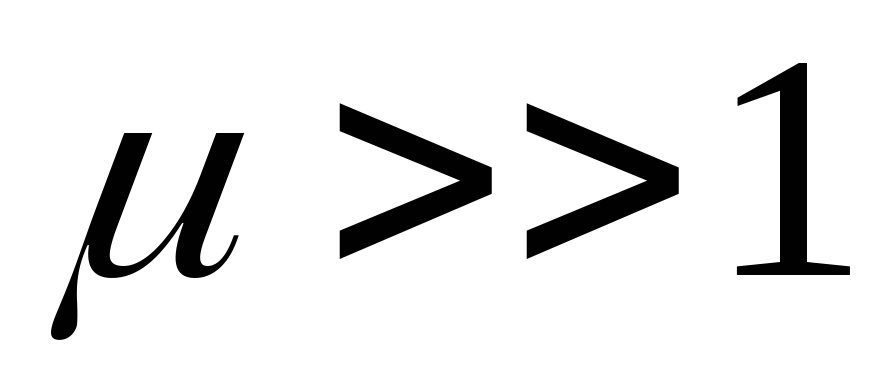Для большинства веществ относительная магнитная проницаемость близка к единице. В таблице 1.2 приведены значения относительной магнитной проницаемости для некоторых веществ.

Таблица 1.2 Относительная диэлектрическая проницаемость

Вещество	Относительная диэлектрическая проницаемость,
Вода Кислород Медь Серебро Алюминий	0,9999905 1,00000191 0,99999044 0,9999736 1,0000222

Формула связи между ив видеуказывает на линейный характер связи. Отметим, что для ферромагнетиков такая связь имеет нелинейный характер.

В ферромагнетиках существуют отдельные микроскопические области (домены), имеющие размеры порядка . Внутри домена все элементарные магнитные моменты параллельны между собой. Поэтому каждый домен ферромагнетика обладает собственным магнитным моментом, величина которого зависит от структуры вещества и не зависит от внешнего поля. Если внешнее магнитное поле отсутствует, то магнитные моменты доменов ориентированны хаотично, а суммарный магнитный момент равен нулю. Если ферромагнетик находится во внешнем магнитном поле, то происходит ориентация магнитных моментов по направлению внешнего магнитного поля.

Уравнения в виде ,называютсяматериальными уравнениями или уравнениями состояния среды. Материальные уравнения справедливы для широкого класса материальных сред, но применимость этих уравнений имеет ограничения, которые следует иметь в виду. Дело в том, что на высоких частотах векторы поляризации и намагничиванияне успевают мгновенно следовать за изменением действующего внешнего поля. В этом случае наблюдается явление запаздывания. В результате параметры среды становятся зависимыми от частоты действующего электромагнитного поля. Такое явление носит названиечастотной дисперсией среды.

Основная особенность материальных уравнений заключается в их линейном характере. При дальнейшем изучении будем полагать, что в рассматриваемых средах выполняется линейность материальных уравнений. Помимо линейных, существуют нелинейные среды. Например, нелинейность среды проявляется при больших значениях напряженности полей. Так, электрическая нелинейность характерна для электромагнитных полей, создаваемых мощными лазерами. Упомянутые выше ферромагнетики проявляют магнитную нелинейность, а сегнетодиэлектрики – электрическую нелинейность среды и при достаточно умеренных значениях напряженностей полей.

9. Классификация сред.

Все среды можно классифицировать в зависимости от выбранного признака, положенного в основание классификации. Различают следующие среды:

• однородные – неоднородные;

• линейные – нелинейные;

• изотропные – анизотропные.

Дадим каждой среде определение.

Однородная среда – это среда, параметры которой (,,) не зависят от координат.

Неоднородная среда – это среда, параметры которой (,,) являются функциями координат.

Линейная среда – это среда, параметры которой (,,) не зависят от внешнего воздействующего поля, а материальные уравнения носят линейный характер.

Нелинейная среда – это среда, параметры которой (,,) зависят от внешнего воздействующего поля.

Изотропная среда – это среда, свойства которой не зависят от направления векторов поля и параметры которой (,,) являются скалярными величинами.

Анизотропная среда – это среда, свойства которой зависят от направления векторов поля и параметры среды (,,) являются тензорными величинами.

9. Уравнения Максвелла в комплексной форме

Выше указывалось, что уравнения Максвелла в дифференциальной форме записи описывают электромагнитные процессы в пространстве и во времени. Иными словами, в описании процесса используют три пространственные координаты и четвертой переменной является время, т. е. необходимо наличие четырех переменных (). Мы учли, что используем декартовую систему координат.

Описать процесс при наличии четырех переменных достаточно сложно. Оказывается, что систему уравнений Максвелла можно записать в иной форме, позволяющей “избавиться” от временной переменной и рассматривать электромагнитный процесс, протекающий в пространстве, только из трех переменных – координат ().

Рассмотрим более подробно вывод новой формы записи уравнений Максвелла. Примем, что сторонние токи отсутствуют. Уравнения Максвелла в этом случае записываются в форме

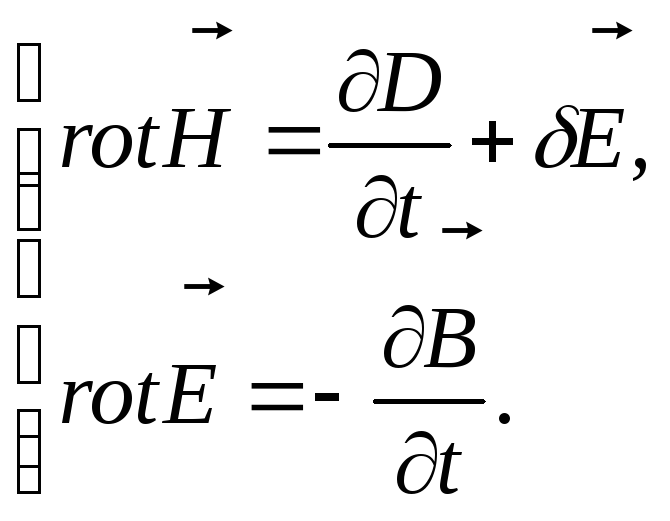
Такая система уравнений записана для мгновенных значений и. Для гармонически изменяющихся во времениизапишем

(1.75)

где - амплитудные значения,- угловая частота,- время,- начальные фазы.

Мгновенные значения напряженности полей (1.75) можно записать в виде

, (1.76)

где - это мнимая часть. Тогда для мгновенных значений напряженностей полей можно записать

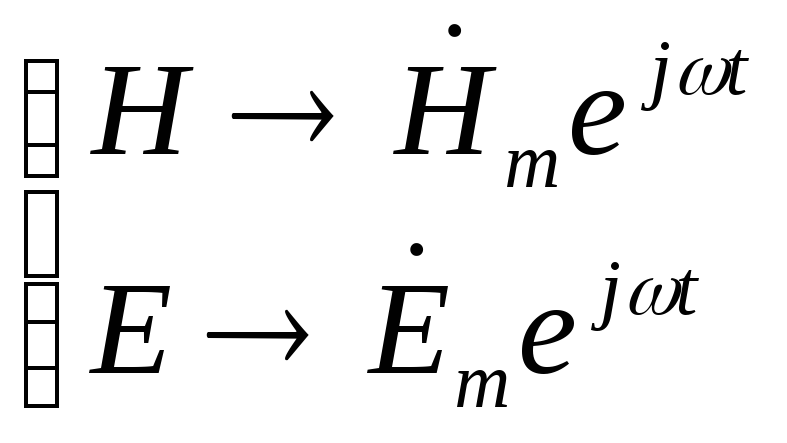
где ,.

Так как напряженности полей являются векторными величинами, то будем обозначать и. Стрелка означает, что речь идет о векторе в пространстве, точка – о том, что проекция вектора на любую координатную ось изменяется с течением времени по синусоидальному закону. Учитывая введенные обозначения, можно для плотности тока проводимости записать:

Плотность тока смещения представим в виде:

.

.

Тогда исходное уравнение Максвелла перепишем в виде

После сокращения получаем формулу

(1.77)

Таким образом, получено уравнение Максвелла в комплексной форме записи.

Сформулируем правило перехода дифференциальной формы уравнений Максвелла к комплексной форме: оператор дифференцирования по времени, действующий на мгновенное значение поля, заменяется на множитель .

Аналогично можно преобразовать остальные уравнения системы. В результате система уравнений Максвелла в комплексной форме записи имеет вид:

,

,

,

, (1.78)

,

.

Таким образом, система уравнений Максвелла имеет три формы записи: интегральную, дифференциальную, комплексную.

9. Сводка уравнений Максвелла

Приведем сводку уравнений Максвелла, являющихся обобщением экспериментальных законов электромагнетизма (таблица 1.3).

Таблица 1.3 Сводка уравнений Максвелла

№ п/п	Форма системы уравнений Максвелла
	Дифференциальная	Интегральная	Комплексная
1
2
3
4
5
6

При решении задач электродинамики часто используется дифференциальная форма уравнений Максвелла, которая представляет собой пространственно-временное описание электромагнитного процесса. Уравнения Максвелла в интегральной форме определяют основные законы электромагнитных процессов. Общую математическую формулировку основных законов электромагнитного поля Максвелл получил в 1873 году. Уравнения Максвелла применяются в случае, если выполняется условие

, (1.79)

где - длина электромагнитной волны,- расстояние между элементарными частицами вещества. Если неравенство (1.79) не выполняется, то уравнения Максвелла не применимы.