
- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
- •Глава 1. Уравнения электромагнитного поля
- •Глава 2. Граничные условия
- •Глава 3. Плоские электромагнитные волны и их свойства
- •Глава 4. Линии передачи электромагнитной энергии
- •Глава 5. Основы распространения радиоволн в свободном пространстве
Глава 2. Граничные условия
Постановка задачи
Распространяясь, электромагнитное поле всегда каким-либо образом испытывает ограничение в пространстве. Естественными границами могут быть, например, металлические стенки или границы раздела между средами с различными параметрами. Если параметры сред на границе раздела изменяются скачкообразно, то компоненты векторов электромагнитного поля также претерпевают разрыв в точках границы. Рассмотрим границу раздела двух сред (рис. 2.1).

1, 1
2, 2

Рис. 2.1. Граница раздела двух сред с различными параметрами
Среда 1 имеет параметры 1, 1; среда 2 имеет параметры 2, 2. На границе раздела выделим произвольную точку P. Пусть известно полное электромагнитное поле в бесконечно малой окрестности этой точки, относящееся к среде 1. Необходимо знать электромагнитное поле в такой же окрестности, принадлежащей среде 2. Именно к нахождению векторов электромагнитного поля во второй среде сводится задача. Стоит отметить, что параметры двух сред отличаются, но незначительно.
Любой вектор в пространстве расположенный отлично от нормали, проведенный к единичной площадке можно разложить на две составляющие: нормальную и тангенциальную.
Решение поставленной задачи поведения векторов электромагнитного поля будет рассмотрено в отдельности для тангенциальных и нормальных составляющих этих векторов на границе раздела двух сред.
Граничные условия для нормальных составляющих магнитного поля
Выделим в окрестностях точки Р достаточно малый цилиндрический объем с основаниями S и образующей h, , чтобы считать векторы магнитной индукции в двух средах постоянными (рис. 2.1).
Для выведения формул используем закон неразрывности силовых линий

Поток вектора
магнитной индукции через суммарную
поверхность запишется как произведение
магнитной индукции
![]() на площадь верхнего и нижнего основания
выделенного цилиндра и поток через
боковую поверхность
на площадь верхнего и нижнего основания
выделенного цилиндра и поток через
боковую поверхность
 поток
через боковую поверхность (2.1)
поток
через боковую поверхность (2.1)
Если устремить образующую h к нулю, приближенное равенство станет более точным и поток вектора магнитной индукции через боковую поверхность станет бесконечно малым, тогда
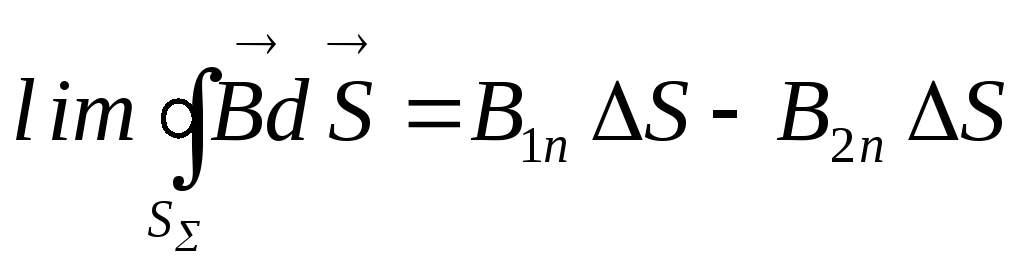 (2.2)
(2.2)
Так как во всех случаях справедлив закон неразрывности силовых линий, запишем
![]()
![]()
![]() (2.3)
(2.3)
Поскольку
![]() ,
,
то можно записать граничные условия для нормальной составляющей вектора напряженности магнитного поля
![]()
 (2.4)
(2.4)
Из выше сказанного, очевидно, что индукция магнитного поля на границе двух сред непрерывна, а напряженность магнитного поля испытывает скачок, который зависит от параметров сред.
Граничные условия для нормальных составляющих электрического поля
Аналогично методике, примененной в предыдущей главе, выведем граничные условия для нормальных составляющих электрического поля.
Поток вектора
индукции через суммарную поверхность
запишется как произведение индукции
электрического поля
![]() на площадь верхнего и нижнего оснований
выделенного цилиндра и поток через
боковую поверхность
на площадь верхнего и нижнего оснований
выделенного цилиндра и поток через
боковую поверхность
 поток
через боковую поверхность (2.5)
поток
через боковую поверхность (2.5)
Так как в случае электрического поля
![]()
В рассматриваемом случае возможны два варианта:
Плотность поверхностных электрических зарядов равна нулю, т.е. = 0.
В соответствии с теоремой Гаусса суммарный заряд, заключенный в рассматриваемой цилиндрической поверхности будет равен
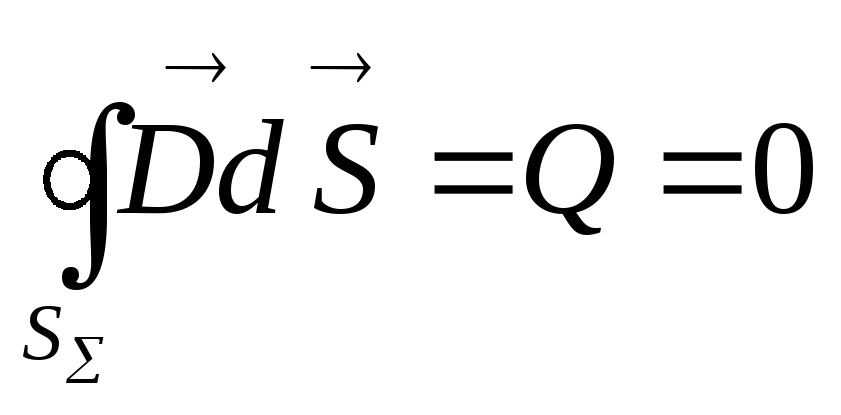
Отсюда
можно записать
![]() (2.6)
(2.6)
Поскольку
![]() можно записать граничные условия для
нормальной составляющей векторов
напряженности электрического поля
можно записать граничные условия для
нормальной составляющей векторов
напряженности электрического поля
![]() (2.7)
(2.7)
Таким образом, при отсутствии поверхностных электрических зарядов на границе раздела двух сред нормальные составляющие индукции электрического поля будут непрерывны, а нормальные составляющие векторов напряженности электрического поля будут испытывать скачок.
На границе раздела равномерно распределен поверхностный электрический заряд, который имеет плотность . Используя закон Гаусса и устремив образующую цилиндра к нулю можно записать
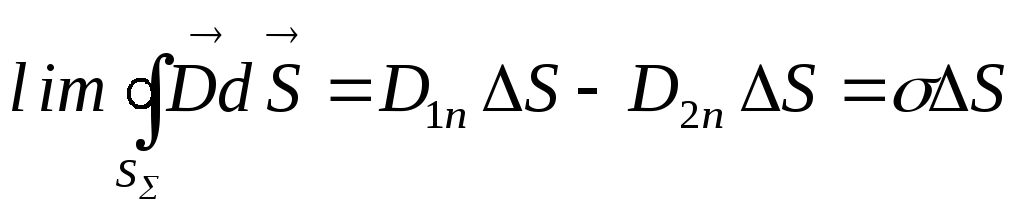 (2.8)
(2.8)
Отсюда получим формулу в виде
![]()

Это означает, что при наличии заряженной границы раздела двух сред нормальные составляющие индукции электрического поля испытывают скачок на величину плотности поверхностного заряда.
Граничные условия для тангенциальных составляющих магнитного поля
Решение задачи о тангенциальных составляющих магнитного поля на границе раздела двух сред решается при помощи закона полного тока для некоторого контура, проведенного в окрестностях точки Р (рис. 2.3).
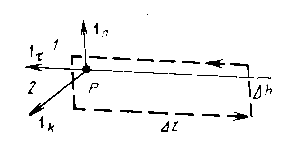
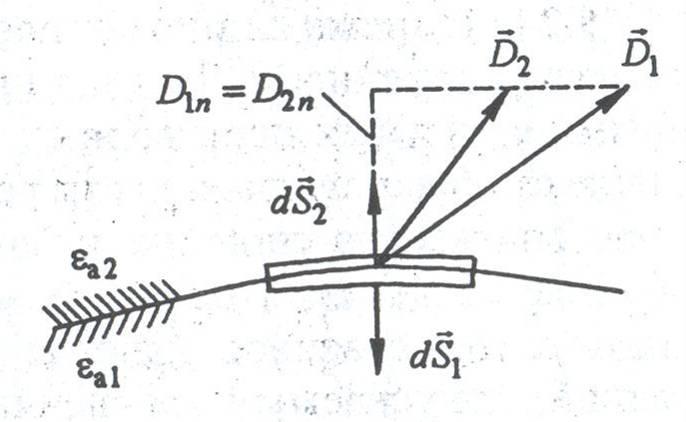
Рис. 2.3 Тангенциальные составляющие электромагнитного поля
Контур расположен перпендикулярно линии раздела двух сред. Направление обхода контура выберем против часовой стрелки.
Применим к рассматриваемому контуру закон полного тока и вычислим циркуляцию вектора напряженности магнитного поля по контуру
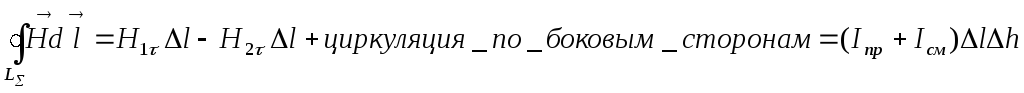 (2.9)
(2.9)
Необходимо рассмотреть два случая:
Параметры обеих сред являются конечными значениями.
При стремлении боковой стороны контура к нулю, циркуляция вектора напряженности магнитного поля по боковым сторонам будет также стремиться к нулю. Учитывая поставленные условия о конечности параметров, имеем
 (2.10)
(2.10)
Отсюда получаем соотношение
![]()

Поскольку
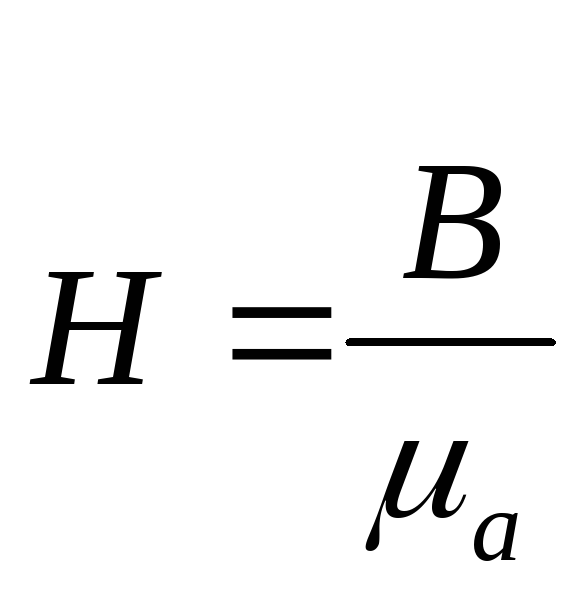
можно записать граничные условия для нормальной составляющей вектора напряженности электрического поля
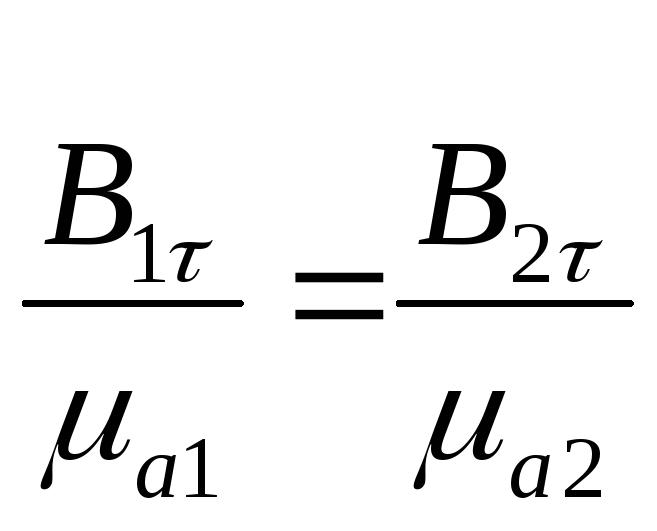
 (2.11)
(2.11)
Таким образом, при конечных значениях параметров двух сред на границе раздела этих сред тангенциальные составляющие напряженности магнитного поля будут непрерывны, а тангенциальные составляющие векторов магнитной индукции терпят разрыв.
Проводимость одной из граничных сред стремится к бесконечности.
При бесконечно большой проводимости, например, второй среды, глубина проникновения электромагнитных волн на любой частоте равна нулю. В результате токи проводимости протекают по поверхности.
Граничные условия для тангенциальных составляющих электрического поля
Решение задачи о тангенциальных составляющих электрического поля на границе раздела двух сред проводится с помощью закона электромагнитной индукции. В соответствии с этим законом для контура (рис. 2.3) можно записать
![]()
 (2.12)
(2.12)
Так как величина
![]() для граничных сред является конечной,
то при стремлении боковой стороны
контура к нулю
для граничных сред является конечной,
то при стремлении боковой стороны
контура к нулю
 (2.13)
(2.13)
Откуда получаем соотношение

![]()
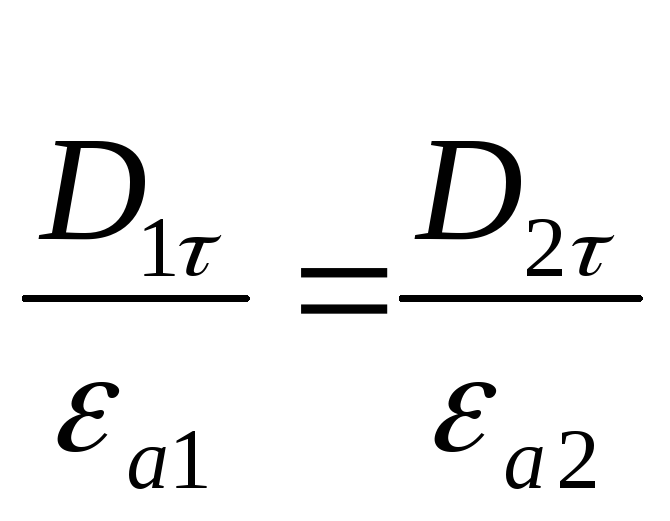
 (2.14)
(2.14)
Таким образом, на границе раздела двух тангенциальные составляющие векторов напряженности электрического поля сред непрерывны, однако тангенциальные составляющие индукции электрического поля претерпевают разрыв.
