Часть 2

Задание

По круглому цилиндрическому проводнику протекает синусоидальный ток i = 4.3sin t, [А]. Радиус проводникаR= 0.0018 [м], удельная проводимость материала= 2·10⁷[См/м], относительная магнитная проницаемость= 1.

1. Определить плотность тока и напряженность магнитного поля внутри проводника. Числовой ответ дать для точек, находящихся на расстоянии от оси провода r = 0; r = 0.25R; r = 0.5R; r = 0.75R; r = R при двух частотах: f = 100 [Гц] и f= 100∙f = 10000 [Гц].

2. Построить графики зависимостей модулей плотности тока и напряженности магнитного поля от r.

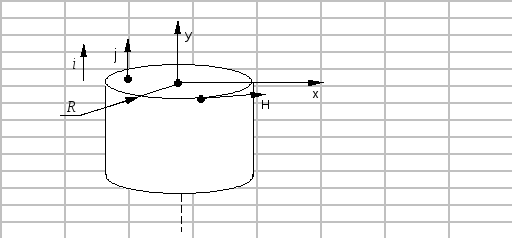
Рисунок 2.1. Проводник по которому течёт ток.

Решение

2.1. Определение плотности тока и напряженности магнитного поля внутри проводника

Электромагнитное поле для неподвижных тел и сред описывается системой уравнений Максвелла:

(1)

(2)

(5)

(3)

(4)

(7)

(6)

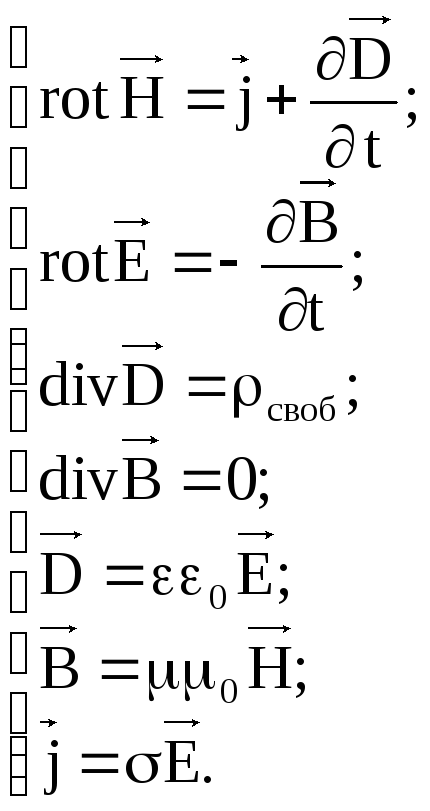
По условию, ток iво времени изменяется по гармоническому закону, значит, связанный сiравенством, изменяется гармонически. Исходя из (7), (5), (1) и (6) заключаем, что изменения,,итакже носят гармонический характер. Следовательно, можно воспользоваться символическим методом расчета.

Пусть – изображение,–,–,–. Операция дифференцирования по времени заменяется умножением на(i- мнимая единица). В нашем случае среда однородная и изотропная. Умножим (2) на σ, и в силу (7) и всего вышеизложенного (2) примет вид:

(8)

.

У

(9)

равнение (1) с учетом (5) и (7):

.

Отношение , значит с большой степенью точностью вторым слагаемым в правой части уравнения (9) можно пренебречь, тогда:

,

или

(10)

.

От обеих частей уравнения (8) возьмем операцию ротора, получим:

.

Д

(11)

алее, исходя из (10) и соотношения, имеем:

.

Возьмем операцию дивергенции от обеих частей (10):

.

Из теории поля известно, что , значит. Тогда (11) примет вид:

(12)

.

В цилиндрических координатах:

.

отиzне зависит и направлено вдоль оси цилиндра. Получаем:

.

Обозначим . Тогда

или

(13)

.

В математике известно, что решение уравнения (13) записывается в виде

,

где J₀(qr)- функция Бесселя нулевого порядка первого рода;

N₀(qr)- функция Бесселя нулевого порядка второго рода.

N₀(qr) приqr=0 обращается в бесконечность. Из физических соображенийвсюду конечен, поэтому принимаемВ = 0.

Из (8) определим , учитывая, что, в цилиндрических координатах:

,

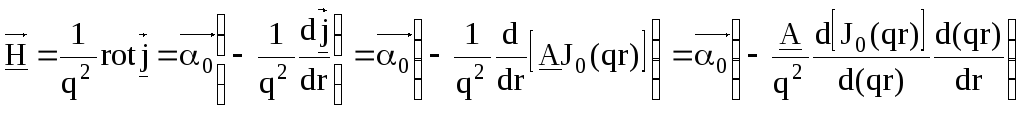где - единичный орт оси 0;

где - функция Бесселя первого порядка первого рода.

(14)

.

Из закона полного тока определимна поверхности провода (приr=R), приравняем его значению, полученному из соотношения (14) и определимA:

,

.

(15)

,

где - единичный орт оси 0z,

(16)

.

2.1.1. Плотность тока и напряженность магнитного поля при частоте f= = 100 Гц

ω = 2πf = 23.14100 = 628.32 рад/с

μ_а = μ₀μ = 4π10^-71 = 12.5610^-7 Гн/м

На поверхности проводника:

.

,

это значение будет во всех последующих расчётах для частоты f.

1.1. При r=0 (В центре проводника).

1.2. При r=0,25R.

1.3. При r=0,5R.

1.4. При r=0,75R.

1.5. При r=R.

Таблица 2.1. Результаты вычислений при частоте f= 100 Гц

r, [м]	qr	Jo(qr)	J1(qr)	jm0, [А/м2]	Hm0, [А/м]
0	0	1	0	425056.4827	0
0.00045	0.056534	1.00000032	0.0282843	425056.6187	95.695564
0.0009	0.113069	1.000005107	0.056569	425058.6534	191.392481
0.00135	0.1696032	1.00002586	0.0848528	425067.4746	287.086353
0.0018	0.22614	1.0000845	0.1124322	425092.3999	380.39632

2.1.2. Плотность тока и напряженность магнитного поля при частоте f= = 10000 Гц

ω = 2πf = 23,1410000 = 62832 рад/с

μ_а = μ₀μ = 4π10^-71 = 12,5610^-7 Гн/м

На поверхности проводника

1.206377,

это значение будет во всех последующих расчётах для частоты f.

2.1. При r=0 (В центре проводника).

2.2. При r=0,25R.

2.3. При r=0,5R.

2.4. При r=0,75R.

2.2. При r=R.

Таблица 2.2. Результаты вычислений при частоте f= 10000 Гц

r, [м]	qr	Jo[qr]	J1[qr]	jm0, [А/м2]	Hm0, [А/м]
0	0	1	0	396144.4097	0
0.00045	0.565344	1.0012	0.283069	396619.783	89.257675
0.009	1.130688	1.024908	0.567881	406011.5747	179.064954
0.00135	1.696032	1.123086	0.86634	444904.2406	273.1754234
0.0018	2.261376	1.358697	1.206377	538240.2211	380.39632