Министерство образования и науки Российской Федерации

Марийский Государственный Технический Университет

Кафедра РТиМБС

Расчетно-графическая работа

по дисциплине

«Основы теории цепей»

Методы формирования уравнений электрического баланса цепей

Выполнил: ст. гр. РТб-21

.

Проверил: к.т.н., доцент

Калачев Е.Н.

Йошкар-Ола

2010

Введение

Данная расчетно-графическая работа выполнена с целью изучения методов формирования уравнений электрического равновесия цепей, которым относятся: метод токов ветвей, метод напряжений ветвей, метод контурных токов и метод узловых напряжений. Метод токов ветвей основан на том, что ток и напряжение каждой ветви, за исключением ветвей, содержащих идеализированные источника тока, а также ветвей, составленных только из идеализированных источников напряжения, связаны между собой однозначной зависимостью, которая определяется компонентным уравнением данной ветви. При составлении системы уравнений электрического равновесия цепи с помощью метода напряжений ветвей в качестве независимых переменных используют неизвестные напряжения р-р_ин ветвей. Метод напряжений ветвей в общем случае нельзя использовать для формирования уравнений электрического равновесия цепей со связанными индуктивностями, так как токи таких индуктивностей могут быть выражены через соответствующие напряжения только при коэффициенте связи между идуктивностями, меньше единицы. Метод контурных токов основан на важной топологической особенности электрических цепей, заключающихся в том, что токи всех ветвей цепи связаны между собой q-1 уравнением баланса токов, и, следовательно, из p токов ветвей только p-q+1 ток может быть задан независимо. При анализе цепей с взаимной индуктивностью целесообразно либо заменять связанные индуктивности участка цепей, не содержащими связанных индуктивностей, либо формировать уравнения равновесия с помощью метода токов ветвей.

1. Метод токов ветвей

Составим основную систему уравнений электрического равновесия цепи для схемы, приведенной на рисунке 1.1. Характеристики элементов цепи предствлены в таблице 1.

I

II

III

Рис. 1.1

Таблица 1

№ Вар.	E1,В	E2,В	E3,В	E4,В	E5,В	E6,В	R1,Ом	R2,Ом	R3,Ом	R4,Ом	R5,Ом	R6,Ом
2	-10	0	10	0	10	0	10	100	10	100	10	100

Количество уравнений, составленных по первому закону Кирхгофа, будет определяется по формуле m = q – 1, где q – количество узлов.

Для данного случая: m = q – 1= 4-1=3;

Для узла (1) -i₁-i₂+i₃=0

Для узла (2) -i₃+i₅+i₆=0

Для узла (3) i₄-i₅-i₆=0

Количество уравнений по второму закону Кирхгофа определяется по формуле:

n = p – q + 1, где p – количество ветвей.

Для данного случая: n = 6 – 4 + 1 = 3;

Для контура I u₁-u₂=0

Для контура II u₂+u₃+u₄+u₅=0

Для контура III -u₅+u₆=0

Количество компонентных уравнений равно числу ветвей. Для данной схемы их число равно 6.

Для первой ветви u₁=i₁R₁-E₁;

Для второй ветви u₂=i₂R₂-E₂;

Для третьей ветви u₃=i₃R₃-E₃;

Для четвёртой ветви u₄=i₄R₄+E₄;

Для пятой ветви u₅=i₅R₅+E₅;

Для шестой ветви u₆=i₆R₆+E₆.

Система уравнений необходимая для расчета данной схемы состоит из 12 уравнений.

Используя метод токов ветвей, найдем напряжение ветвей для данной электрической цепи.

Подставляя компонентные уравнения в уравнения, составленные по второму закону Кирхгофа, получаем в сочетании с уравнениями по первому закону Кирхгофа сокращенную систему уравнений электрического равновесия цепи:

i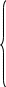 ₁R₁-E₁-(i₂R₂-E₂)=0;

i₂R₂-E₂+i₃R₃-E₃+i₄R₄+E₄+i₅R₅+E₅=0;

-(i₅R₅+E₅)+i₆R₆+E₆=0;

-i₁-i₂+i₃=0;

-i₃+i₅+i₆=0;

i₄-i₅-i₆=0;

1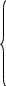 0i₁+10-100i₂=0;

100i₂+10i₃-10+100i₄+10i₅+10=0;

-10i₅-10+100i₆=0;

-i₁-i₂+i₃=0;

-i₃+i₅+i₆=0;

i₄-i₅-i₆=0;

Расчеты выполнены в MathCAD 14 Pro

i₁ =-0,149 А;

i₂ =0,085 А;

i₃ =-0,064 А;

i₄ =-0,064 А;

i₅ =-0,149 А;

i₆ =0,085 А.

Подставляя данные значения токов в компонентные уравнения, находим напряжения ветвей:

u₁ =8,511 В;

u₂ =8,511 В;

u₃ =-10,638 В;

u₄ =-6,383 В;

u₅ =8,511 В;

u₆ =8,511 В.