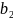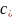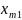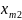Транспортная задача.
Цель транспортной задачи состоит в разработке наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
Общая постановка
транспортной задачи состоит в следующем:
в
пунктах производства
имеется однородный груз в количестве
соответственно
.
Этот груз необходимо доставить в
пунктов назначения
в количестве соответственно
.
Стоимость перевозки единицы груза
(тариф) из пункта
в пункт
равна
.
Требуется составить план перевозок,
позволяющий вывести все грузы и имеющий
минимальную стоимость.
Общее наличие груза
у поставщиков рано
,
общая потребность в грузе в пунктах
назначения равна
,
тогда, если
,
то задача называется закрытой. Если
,
то открытой. Обозначим через
количество груза перевозимого из
в пункт
.
Запишем условие задачи в виде таблицы.
|
|
|
… |
|
… |
|
|
|
|
… |
|
|
|
||
|
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
.. |
|
Транспортная задача как ЗЛП может быть решена симплексным методом, но для решения транспортной задачи разработан специальный метод, имеющий те же этапы, что и симплексный, а именно:
– нахождение исходного опорного решения;
– проверка этого решения на оптимальность;
– переход от одного опорного плана к другому.
Нахождение исходного опорного плана.
Условие задачи и ее
исходное опорное решение будем записывать
в распределительную табл. Существует
несколько способов нахождения исходного
опорного решения. Рассмотрим один из
них – метод минимального тарифа (
элемента). Согласно этому методу, грузы
распределяются в первую очередь в те
клетки, к которых находится минимальный
тариф перевозок
.
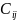Далее поставки распределяются в незанятые
клетки с наименьшими тарифами с учетом
оставшихся запасов у поставщиков и
удовлетворения спроса потребителей.
Процесс распределения продолжается до
тех пор, пока все грузы от поставщиков
не будут вывезены, а потребители не
будут удовлетворены. При распределении
грузов может оказаться, что кол-во
занятых клеток меньше, чем
. В этом случае недостающее их число
заполняется клетками с нулевыми
поставками.
Пример.
Решение.
Проверяем, является ли данная задача закрытой или открытой. Для этого находим
,
,
т.к.
,
то
данная задача закрытая. Найдем исходное
решение методом минимального тарифа.
-
140
300
160
90
2
90
5
2
400
4
1
300
5
100
110
3
50
6
8
60
Т.к. число заполненных клеток равно 5 и m+n-1=3+3-1=5, то план невырожденный. Полученное исходное опорное решение имеет вид:
.
Стоимость
перевозки при данном опорном плане
составит:
усл.ден.ед.
Проверка опорного плана на оптимальность.
Найденное
исходное опорное решение проверяем на
оптимальность. Для проверки оптимальности
плана воспользуемся методом потенциалов.
Для этого в таблице добавим строку
и столбец
.
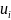Потенциалы будем находить и равенства
для заполненных клеток. Числа
и
называются потенциалами. Одному из
потенциалов припишем произвольное
значение, например
,
тогда остальные потенциалы определяются
однозначно. Если известен потенциал
то
,
если известен потенциал
то
.
После того, как все потенциалы найдены,
найдем
.
Эту оценку называют оценочной. Если для
всех незаполненных клеток
,
то полученный план является оптимальным,
если хотя бы одна оценка
,
то опорный план оптимальным не является
и его можно улучшить. Если хотя бы одна
оценка равна нулю то ТЗ имеет бесчисленное
множество решений.
-
140
300
160
90
2 –
90
5
2 +
2
400
4
1
300
5
100
0
110
3 +
50
6
8 –
60
3
0
1
5
Найдем превышения для незаполненных клеток:
;
;
;
.
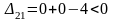Т.к.
,
следовательно, исходное опорное решение
оптимальным не является. Необходимо
перейти к другому опорному решению. Для
этого надо перераспределить грузы,
перемещая их из занятых клеток в
свободные. Для свободной клетки с
строим цикл (замкнутая ломаная линия),
все вершины которого кроме одной лежат
в занятых клетках, углы прямые, число
вершин четное. В свободной клетке цикла
ставим знак «+», затем поочередно
проставляем знаки «-» и «+». Из всех
вершин со знаком
«-»
выбираем наименьший груз. В клетки со
знаком «+» добавляем этот груз, а у клеток
со знаком «-» отнимают этот груз. В
результате перераспределения груза
получим новый опорный план. Полученное
решение проверяем на оптимальность и
т.д., пока не получим оптимальное решение.
В нашем примере имеем
.
|
|
|
|
|
|||
140 |
300 |
160 |
|||||
|
90 |
2 – 30 |
5 |
2 + 60 |
0 |
||
|
400 |
4 +
|
1 300 |
5 – 100 |
3 |
||
|
110 |
3 110 |
6 |
8
|
1 |
||
|
2 |
-2 |
2 |
|
|||
;
;
;
.
.
-
140
300
160
90
2
5
2
90
-3
400
4
30
1
300
5
70
0
110
3
110
6
8
-1
4
1
5
;
;
;
.
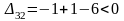Т.к. все оценки свободных клеток отрицательны, следовательно, полученное решения является оптимальным.
.
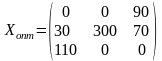При
этом стоимость транспортных расходов
равна
(
усл. ден.ед.). По сравнению с исходным
планом стоимость уменьшилась на
1610–1280=330 усл.ден.ед. Мы рассмотрели
задачу закрытого типа и имеющую
невырожденное решение. При решении
транспортных задач может оказаться,
что число занятых клеток меньше, чем
m+n-1
,
тогда задача имеет вырожденное решение.
Для ее решения необходимо в свободную
клетку с наименьшим тарифом ввести
нулевую поставку. При открытой ТЗ
,
необходимо ввести фиктивного потребителя,
если
или
фиктивного поставщика, если
.
Для
ТЗ также можно дать экономический
анализ. А также отметим, что алгоритм и
методы решения ТЗ могут быть использованы
при решении некоторых экономических
задач, не имеющих ничего общего с
транспортировкой груза. В этом случае
величины тарифов
имеют
различный смысл в зависимости от
конкретной экономической задачи.
Например: 1) оптимальное закрепление за
станками операций по обработке деталей;
2) увеличение производительности
автомобильного транспорта за счет
минимизации порожнего пробега и т.д.