Приведение общей злп к каноническому виду.
Общий вид ЗЛП следующий:
(
1 )
(
2 )
(
3 )
где соотношение ( 1 ) – целевая функция, ( 2 ) – система основных ограничений , ( 3 ) – система дополнительных ограничений.
Соотношения ( 2 ) и ( 3 ) образуют полную систему ограничений.
Приведение
системы основных ограничений к
каноническому виду осуществляется
введением в левые части неравенств
дополнительных неотрицательных
переменных с коэффициентами «+1», если
неравенства вида
и «-1», если неравенства вида
. В целевую функцию дополнительные
переменные входят с нулевыми коэффициентами.
Определение. ЗЛП называется заданной в каноническом виде, если ее система основных ограничений представлена уравнениями.
Определение. ЗЛП называется заданной в стандартной форме канонического вида, если выполняются следующие условия:
система основных ограничений представлена уравнениями и все они линейно независимы;
число уравнений меньше числа переменных;
решается задача минимизации целевой функции;
правые части системы основных ограничений неотрицательны;
все переменные также неотрицательны.
Формы записи злп. Основные определения.
Существуют несколько форм записи ЗЛП.
Развернутая форма записи:
Форма записи с помощью знаков суммирования имеет вид:
Матричная форма записи ЗЛП:
Обозначим
через
– матрицу системы основных ограничений;
– матрицу–столбец
неизвестных;
– матрицу–строку
коэффициентов при неизвестных в целевой
функции;
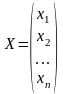– матрицу–столбец
свободных чисел.
Тогда ЗЛП можно записать в следующим образом:
Векторная форма записи ЗЛП:
;
;
;
;…….;
;
Тогда
Определение.
Планом
ЗЛП
называется набор значений переменных
,
удовлетворяющий полной системе
ограничений.
Определение. Решением ЗЛП или оптимальным планом, называется план, доставляющий целевой функции заданный вид экстремума.
Определение. План ЗЛП называется опорным, если его положительным компонентам соответствует система линейно независимых векторов.
Определение. Опорный план ЗЛП называется невырожденным, если векторы, соответствующие его положительным компонентам, образуют базис.
В противном случае опорный план называется вырожденным.
Методы решения задач линейного программирования
Графоаналитический метод решения злп.
Графоаналитический метод решения есть наиболее простым и наглядным метолом линейного программирования. Этот метод применяется, в основном, для решения ЗЛП с двумя переменными и только иногда для решения задач трехмерного пространства.
Можно выделить два способа графоаналитического решения ЗЛП: способ полного перебора и способ направленного перебора, или градиентный способ.
Алгоритм решения задач.
Способ полного перебора.
Находим область допустимых решений системы ограничений задачи, т.е. строим множество
и оцениваем его:
а)
если
(пустое мн–во), то решений нет;
б) если – выпуклая многогранная область, то метод не применим;
в) если – выпуклый многоугольник, то переходим к следующему этапу решения.
Определяем координаты угловых точек множества .
Вычисляем значение целевой функции в каждой точке множества и определяем точки экстремума:
если требуемый экстремум достигается в одной точке, то ЗЛП имеет единственное решение и координаты этой точки являются оптимальным планом;
если требуемый экстремум достигается в двух угловых точках, то ЗЛП имеет бесчисленное множество решений, которыми являются координаты любой точки отрезка, соединяющие данные угловые точки.
Способ направленного перебора.
Строим множество и оцениваем его:
а) если , то решений нет;
б) если – выпуклый многоугольник или выпуклая многогранная область, то переходим ко второму этапу решения.
Строим вектор–градиент
,
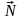.Проводим линию уровня
, которая перпендикулярна вектору
.Линию уровня перемещаем по направлению вектора , ели задача на максимум и в направлении противоположном , для задачи на минимум, до тех пор пока она не станет опорной для множества .
Определение. Прямая называется опорной для многоугольника, если:
Она имеет общие точки с этим многоугольником;
Все точки этого многоугольника лежат по одну сторону от этой прямой.
Находим координаты точки экстремума и вычисляем значение целевой функции в ней.