§ 3.11. Диспетчирование на основе динамических приоритетов

В дисциплинах обслуживания, рассмотренных ранее, приоритеты присваивались заявкам заранее и сохраняли постоянство в течение всего времени работы цифровых управляющих систем (ЦУС). Такого рода приоритеты принято называть статическими, чем подчерки­вается их постоянство во времени. Статические приоритеты не во всех случаях позволяют удовлетворить требованиям к временам ожидания заявок. Так, может оказаться, что доли заявок различ­ных типов в общем потоке заявок изменяются во времени, что сильно затрудняет возможность корректного назначения приоритетов. Иногда важность заявок, под­тверждаемая их приоритетами, может изменяться в зависимости от времени пребывания заявок в очередях: чем дольше заявка ждет, тем более важной она становится. В таких случаях жела­тельно вносить изменения в распреде­ление приоритетов, присваивая более высокие приоритеты заявкам, время ожидания которых приближается к предельно допустимому. При этом це­лесообразно использовать дисциплины обслуживания с изменяющимися во времени приоритетами, называемыми динамическими.

Дисциплины обслуживания с дина­мическими приоритетами — более слож­ные в реализации по сравнению с ди­сциплинами обслуживания со статиче­скими приоритетами, что влечет за собой увеличение непроизводительных затрат времени процессора.

Характеристики ЦУС с двумя потоками заявок. Аналитическое исследование дисциплин обслуживания с динамическими приорите­тами весьма сложно и приводит к громоздким математическим выкладкам. Поэтому ограничимся рассмотрением случая, когда в ЦУС поступает только два потока разнотипных заявок и приори­теты заявок изменяются в зависимости от длительности их ожида­ния в очереди. При этом будем полагать, что длительность обслу­живания заявок имеет произвольное распределение B_i() со сред­ним значением _i (i=1, 2) и выбор заявок на обслуживание осу­ществляется с учетом текущего значения функции приоритетности q_i(t), зависящей для каждой заявки от времени ожидания:

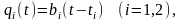
где b_i — коэффициент, определяющий скорость изменения приори­тетности заявки i-го типа в зависимости от времени ожидания; t_i — момент поступления заявки i-го типа в систему; t — рассматри­ваемый (текущий) момент времени (здесь t пробегает значения от t_i до момента окончания обслуживания этой заявки и =t-t_i— время пребывания заявки в системе, определенное на текущий момент времени t).

На рис. 3.28 показано взаимодействие между функциями при­оритетности для двух типов заявок при b_i>0. До момента вре­мени t* заявка второго типа с функцией приоритетности q₂(t) имеет более высокий приоритет по отношению к заявке первого типа с функцией приоритетности q₂(t). В момент времени t* приоритеты заявок обоих типов одинаковы. При t>t* заявка первого типа обладает более высоким приоритетом по сравнению с заявкой второго типа, несмотря на то, что она поступила в систему позже последней. Заявки с малым коэффициентом b_i, при достаточно длительном ожидании могут получить больший приоритет, чем за­явки других типов.

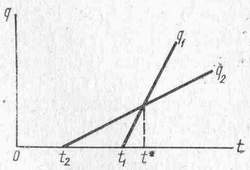
Рис. 3.28. Изменение функ­ций приоритетности во вре­мени

Рассмотрим дисциплину обслужива­ния, построенную на основе динамиче­ских приоритетов, не прерывающих начатого обслуживания, т. е. дисцип­лину с динамическими относительными приоритетами. Вывод выражений для среднего времени ожидания заявок различных типов будем про­водить в предположении, что коэффициенты b_i связаны соотноше­нием b1b20 (рис. 3.28).

Допустим, что в некоторый произвольный момент времени в систему поступила заявка первого типа. Ее время ожидания

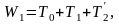(3.23)

где Т₀ — время, необходимое для завершения обслуживания ранее выбранной заявки; T₁ — время обслуживания всех заявок первого типа, поступивших в систему раньше рассматриваемой заявки; Т’₂ — время обслуживания заявок второго типа, которые начнут обслуживаться ранее рассматриваемой заявки.

По аналогии, рассматривая момент поступления заявки второго типа, для времени ожидания можно записать

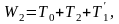(3.24)

где Т₂ — время обслуживания всех заявок второго типа, посту­пивших в систему раньше рассматриваемой заявки; Т’1 — время обслуживания заявок первого типа, которые будут обслуживаться ранее рассматриваемой заявки.

Переходя в (3.23) и (3.24) к математическим ожиданиям, полу­чим систему

(3.25)

Среднее время обслуживания заявок типа k = 1, 2, поступивших в систему раньше рассматриваемой заявки того же типа, Е[T_k]=_kl_k где l_k — среднее число заявок в очереди.

Поскольку l_k=_k_k, то

(3.26)

В свою очередь Е[T’₂]=₂l’₂, где l’₂—число заявок второго типа, которые будут обслужены ранее рассматриваемой заявки первого типа. Если t₁ — момент поступления рассматриваемой заявки первого типа (рис. 3.28), то ранее данной заявки будут обслужены все заявки второго типа, которые поступят в систему до момента t₂. Очевидно, что число этих заявок l’₂= l₂-l₂, где l₂ — число заявок второго типа, находящихся в очереди на момент времени t₁ и l₂ — число заявок второго типа, поступивших в систему за про­межуток времени =t₁-t₂. Тогда l₂=₂₂ и l₂=₂(t₁ - t₂).

Определим величину промежутка времени =t₁-t₂. Из рис. 3.28 следует, что

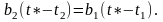
С учетом того, что

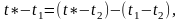
получим

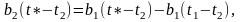
откуда

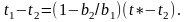
Поскольку момент времени t₂ соответствует моменту поступле­ния последней заявки второго типа, которая будет обслужена раньше заявки первого типа, поступившей в систему в момент t_l то t* - t₂=₂ т, е. разность t* - t₂ равна среднему времени ожи­дания заявки второго типа. Тогда

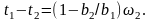(3.27)

Таким образом,

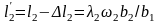
и

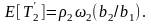(3.28)

По аналогии выведем выражение для Е[T’₁]=₁l’₁ где l’₁ — число заявок первого типа, которые будут обслужены ранее рас­сматриваемой заявки второго типа. Такими заявками являются все заявки l₁, поступившие на момент времени t₂, плюс заявки l_l, поступившие за промежуток времени =(t₁ - t₂), т. е. после поступ­ления рассматриваемой заявки:

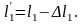
По определению, l₁=₁₁ и l₁=₁(t₁ - t₂). Используя (3.27), получим

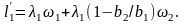
Тогда

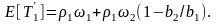(3.29)

Подставляя (3.26), (3.28) и (3.29) в (3.25), получим

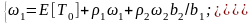
Решая эту систему уравнений относительно _l и ₂, получим

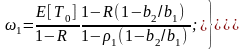(3.30)

Здесь Е[T₀]=(₁₁⁽²⁾+₂₂⁽²⁾)/2 и R=₁+₂— суммарная загрузка системы.

Согласно введенному предположению, (b₂/b₁)1 и, следовательно, ₁₂. Отношение ₂/₁=l/[l-R(1-b₂/b₁] показывает, во сколько раз время ожидания заявок второго типа больше времени ожидания заявок первого типа, и зависит от значений коэффици­ентов b₁, b₂ и суммарной загрузки R. Анализ зависимости ₂/₁ (рис. 3.29) показывает, что при больших значениях отношения =b₂/b₁ средние времена ожидания заявок первого и второго типов различаются незначительно, в то время как при малых значениях  это различие существенно, причем с ростом суммарной загрузки при постоянном  указанное различие увеличивается.

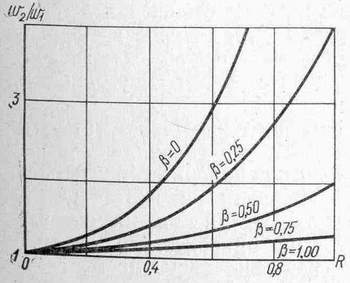
Рис. 3.29. Зависимость отношения времени ожидания заявок ₁/₂ от загрузки R

При b₁=b₂ из (3.30) имеем

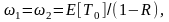
т. е. имеем выражение для бесприоритетной дисциплины обслужи­вания, когда времена ожидания заявок обоих типов одинаковы. Если b₂=0, т. е. функция приоритетности заявок второго типа на любой момент времени q₂(t)=0, из (3.30) получим выражения для среднего времени ожидания в случае дисциплины с фиксирован­ными относительными приоритетами:

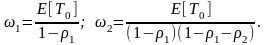
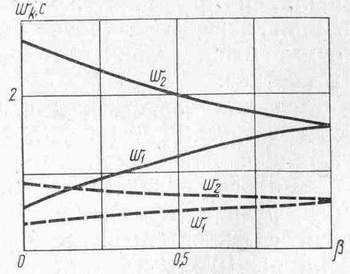
Рис. 3.30. Зависимость среднего времени ожидания _k от отношения коэффициентов =b₂/b₁

На рис 3.30 приведена зависимость среднего времени ожидания _k от отношения коэффициентов b₂/b₁ в случае двух одинаковых потоков заявок, каждый из которых создает загрузку , причем длительности обслуживания распределены по экспоненциальному закону с одинаковым средним =0,4 с. Сплошная линия соответ­ствует суммарной загрузке R=2=0,8, штриховая — R=0,6. Рису­нок наглядно иллюстрирует уменьшение разброса времени ожида­ния заявок различных типов с увеличением отношения b₂/b₁. При одних и тех же значениях отношения b₂/b₁ разброс времени ожи­дания заявок различных типов существенным образом зависит от суммарной загрузки системы R, причем с ростом R. увеличивается и разброс.

Рис. 3.31. Зависимость среднего времени ожидания _k от суммар­ной загрузки R

Анализ зависимости среднего времени ожидания _k от суммар­ной загрузки R (рис. 3.31) показывает, что дисциплина обслужи­вания с динамическими относительными приоритетами (сплошная линия) не обладает свойством устойчивости к кратковременным перегрузкам (R1), присущим, в частности, дисциплине обслужива­ния с фиксированными относительными приоритетами (штриховая линия). Здесь же для сравнения показана зависимость среднего времени ожидания заявок от загрузки системы при использовании бесприоритетной дисциплины обслуживания (штрихпунктирная линия).

Пример 3.7. Рассмотрим ЦУС, реа­лизующую две обслуживающие програм­мы со средней трудоемкостью ₁ = 10000 операций и ₂ = 5000 операций. Програм­мы инициируются с интенсивностями ₁=1 с^-1 и 2 = 7 с^-1.

Пусть используется дисциплина об­служивания с динамическими относитель­ными приоритетами. Рассмотрим два случая назначения коэффициентов b_i: 1) b₁>b₂, причем b₂/b₁=0,5; 2) b₁<b₂, причем b₂/b₁ = 2. Примем, что время вы­полнения программ распределено по экс­поненциальному закону со средними _i=_i/B, где В — быстродействие про­цессора ЦУС. Для экспоненциального закона второй начальный момент _i⁽²⁾=2_i².

Рис. 3.32. Зависимость среднего времени ожидания  от быстро­действия В процессора

(_i^0,5 и _i² — время ожидания заявок типа i=1, 2, соответствующих b₂/b₁=0,5 и b₂/b₁=2)

Определим время ожидания и время пребывания заявок для различных зна­чений быстродействия процессора: 50 тыс., 60 тыс., . . . , 100 тыс. операций/с. На рис. 3.32 показана зависимость среднего времени ожидания заявок от быстро­действия процессора для двух указанных случаев. Из рисунка видно, что для второго случая назначения коэффициентов b_i(b₁<b₂) время ожидания заявок вто­рого типа уменьшилось по сравнению с первым случаем назначения коэффициен­тов b_i(b₁>b₂) за счет увеличения времени ожидания заявок первого типа.

Рис. 3.33. Зависимость отношения среднего времени ожидания ₂/_l от быстродействия В процессора

Рис. 3.33 иллюстрирует характер изменения отношения времени ожидания заявок обоих типов при втором случае назначения коэффициентов b_i ко времени ожидания заявок тех же типов при первом случае в зависимости от быстродей­ствия процессора. Рассматриваемое отношение _i²/_i¹ характеризует степень раз­личия в качестве обслуживания заявок для двух случаев назначения коэффициен­тов b_i. Это различие уменьшается с увеличением быстродействия В процессора. Данный факт легко объясним, если вспомнить, что увеличение быстродействия процессора при неизменных остальных параметрах эквивалентно уменьшению суммарной загрузки системы и, следовательно, больший процент заявок обоих типов будет принят к обслуживанию либо немедленно, если в системе нет заявок, либо с незначительной задержкой.

Характеристики ЦУС с несколькими потоками заявок. В случае нескольких потоков заявок (М>2) среднее время ожидания в оче­реди заявок k-го типа может быть определено по рекуррентной формуле

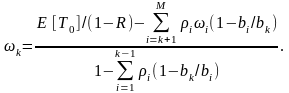(3.31)

При этом предполагается, что . Доказательство выражения проводится аналогично изложенной методике и характеризуется лишь более сложными математическими выкладками.

Кроме рассмотренной дисциплины обслуживания заявок с динамическими относительными приоритетами в ЦУС могут использоваться дисциплины обслуживания с динамическими абсолютными и смешанными приоритетами. В дисциплинах с динамическими абсолютными приоритетами происходит прерывание обслуживаемой заявки, если функция приоритетности какой-либо заявки, находящей­ся в очереди, превысит функцию приоритетности обслуживаемой за­явки.

Используя вышеизложенную методику, можно доказать, что сред­нее время ожидания в очереди заявок k-го типа определяется сле­дующей рекуррентной формулой:

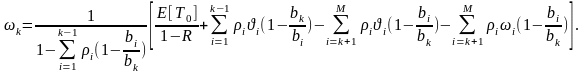
Рассмотрим дисциплину обслуживания заявок, представляющую собой комбинацию дисциплин со статической и с динамической фиксацией приоритетов. Для этого запишем функцию приоритетности, в следующем виде:

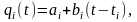
где a_i и b_i — некоторые коэффициенты; t — текущий момент времени, изменяющийся от момента поступления заявки i-го типа t_i до мо­мента окончания обслуживания этой заявки (t=l, ..., М).

Дисциплина обслуживания с такой функцией приоритетности об­ладает многими интересными свойствами и является более общей по отношению к рассмотренным дисциплинам: если коэффициент b_i ра­вен нулю, то данная дисциплина вырождается в дисциплину со ста­тической фиксацией приоритетов, и если коэффициент а_i равен нулю, то имеет место дисциплина с динамической фиксацией при­оритета; варьированием коэффициентов a_i и b_i могут быть получены некоторые выше рассмотренные дисциплины.

Дисциплины обслуживания с динамическими приоритетами более сложны в реализации, чем дисциплины со статической фиксацией приоритетов. Это выражается в дополнительных аппаратурных и программных затратах, что приводит, в свою очередь, к значитель­ным непроизводительным издержкам времени процессора на диспетчирование. Поэтому использование дисциплин обслуживания с дина­мическими приоритетами в ЦУС оправдано лишь в тех случаях, когда параметры входных потоков заявок довольно резко меняются во времени, в связи с чем не могут быть использованы дисциплины с фиксированными приоритетами.