§ 3.9. Обслуживание заявок в групповом режиме

Если управляющая программа включается в работу каждый раз, когда закончено обслуживание очередной заявки, то говорят, что обслуживание выполняется в одиночном режиме. В этом режиме на обслуживание выбирается всегда только одна заявка; управляющая программа исполняется процессором многократно, что приводит к большим затратам процессорного времени на диспетчирование. Непроизводительные затраты процессорного времени можно уменьшить, если назначать на обслуживание сразу группу заявок, стоящих в очереди и имеющих максимальный в данной ситуации приоритет. Такой режим обслуживания заявок называется групповым.

Циклическое обслуживание. При групповом режиме может исполь­зоваться бесприоритетное обслуживание заявок, называемое цикли­ческим. При циклическом обслуживании для заявок типа 1, ..., М выделяются очереди O₁, ..., О_M (рис. 3.25). Сначала обслуживаются все заявки из очереди O₁ затем из очереди O₂ и т. д. После обслу­живания очереди О_M процесс обслуживания вновь возвращается к заявкам из очереди О₁. Такой порядок обслуживания характери­зуется минимальными затратами на диспетчирование.

Рис. 3.25. Циклическое обслу­живание заявок

Аналитическое исследование циклического обслуживания заявок в групповом режиме при произвольном количестве входных потоков весьма сложно и приводит к громоздким результатам. Однако при М=2 известны выражения для средних значений времени ожидания в очереди заявок каждого потока при условии, что время обслужи­вания заявок имеет произвольное распределение:

Анализируя выражения (3.20), можно сделать вывод, что выра­жения для времени ожидания симметричны относительно индексов входящих потоков. Среднее время ожидания в очереди любой заявки из суммарного потока одинаково и рав­но

где =₁+₂.

Дисциплина обслуживания с че­редующимися приоритетами. При групповом обслуживании очередям заявок могут присваиваться относи­тельные приоритеты. Тогда по окон­чании обслуживания всех заявок из очереди O_i управляющая програм­ма последовательно проверяет со­стояние очередей O₁, ..., О_M. Если первой непустой является очередь О_j, то система начинает обслу­живать эту очередь, пока она не будет исчерпана. Дисциплина обслуживания в групповом режиме с относительными приоритета­ми заявок называется дисциплиной с чередующимися приоритетами.

Дисциплина обслуживания по расписанию. В цифровых управ­ляющих системах (ЦУС) для групповой обработки заявок широко используется обслуживание по расписанию, которое организуется следующим образом. Расписание задается в виде (i₁, i₂, ..., i_G), где i_g(g=1, ..., G) — номер очереди, равный 1, ..., H, и G — длина цикла. Например, если число очередей H=4, то расписание может иметь следующий вид: (1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3). Здесь длина цикла G=12. Расписание задает порядок обращения к очередям заявок. Так из приведенного расписания следует, что цикл обслужи­вания начинается с очереди 1, затем обслуживается очередь 2, затем вновь очередь 1 и т. д. Цикл заканчивается обслуживанием очереди 3, после чего ЦУС повторяет цикл обслуживания. За один цикл обслуживания производится шесть обращений к очереди 1, три обращения к очереди 2, два обращения к очереди 3 и одно — к очереди 4. Таким образом, очередь 1 обслуживается наиболее интен­сивно и среднее время ожидания заявок типа 1 уменьшается по сравнению с заявками других типов.

Обслуживание по расписанию отличается гибкостью, позво­ляющей широко варьировать приоритетами заявок. Расписание строится следующим образом. Заявки, поступающие в систему, разделяются на классы. В один класс объединяются разнотипные заявки, для хранения которых выделяется одна очередь. За счет этого уменьшается количество очередей и сокращаются непроизводи­тельные затраты времени на диспетчирование. Число очередей (классов) заявок ЗНМ, где М — число типов заявок, обслужи­ваемых системой. Число классов Н не может быть меньше трех, поскольку при Н=1 расписание вырождается в бесприоритетную дисциплину обслуживания, при Н=2 имеет место диспиплина цик­лического обслуживания.

Обозначим через g_h — число обращений к h-и очереди в одном цикле. Тогда величину

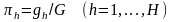
можно трактовать как вероятность обращения к h-й очереди. Очевидно, что

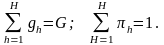
Определим понятие подцикла, которое в дальнейшем понадобится для построения расписания. Пусть h* — номер очереди, для которой число обращений в цикле максимально, т. е. g_h*=max (g₁, ...,g_H). Подциклом называют обращения к очередям, заключенные между двумя последовательными обращениями к очереди h*, включая также одно обращение к этой очереди. Значение g_h* определяет количество подциклов в расписании.

Например, для расписания

(1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, 5, 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2) (3.21)

число обращений g_h к очередям h=1, ..., 5 равно соответственно 15, 8, 4, 2, 1 и длина цикла G=g₁+...+g₅=30. В таком случае вероят­ности обращения к очередям ₁=15/30; ...; ₅=1/30. Отсюда следует, что h*=1 и количество подциклов для данного расписания будет 15.

Поскольку нумерация очередей производится таким образом, что g₁>g₂>...>g_H;, то max (g_l ..., g_H)=g₁ и, следовательно, h* = 1.

К расписанию предъявляют следующие требования: 1) в цикле два последовательных обращения к одной очереди не должны быть расположены рядом, так как в противном случае второе обращение всегда будет осуществляться к пустой очереди; 2) обращения к одной и той же очереди должны быть равномерно распределены по всему циклу, чтобы при каждом обращении к одной и той же очереди число заявок в ней было приблизительно постоянным.

Каноническое расписание. Каноническое расписание — расписание, для которого число обращений к очередям определяется следующим образом:

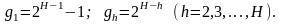(3.22)

Тогда количество обращений к каждой последующей очереди в два раза меньше, чем к предыдущей, и к последней очереди с номером Н производится одно обращение за цикл. Длина цикла канонического расписания

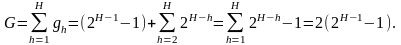
Для расписаний с параметрами (3.22) указанные требования всегда могут быть выполнены. Расписание (3.21) — пример канониче­ского расписания.

Расписание целесообразно представлять в виде матрицы S=[s_ij]. Число строк в матрице равно количеству подциклов в расписании, а число столбцов — количеству классов заявок. Элементы матрицы 0 или 1. Если в подцикле i=l, ..., g_h* должно производиться обра­щение к классу (очереди) h=1, ..., Н, то элемент s_ih=l, в противном случае элемент s_ih=0. Расписанию (3.21) соответствует следующая матрица:

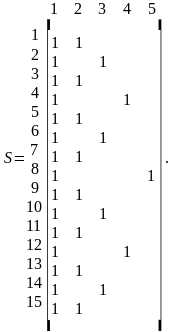
Здесь количество единиц в каждом столбце матрицы соответ­ствует количеству обращений g_h к классу заявок h за один цикл работы системы.

Получение точных аналитических зависимостей, связывающих время ожидания заявок с числом обращений, — сложная задача, которая не может быть решена классическими методами теории мас­сового обслуживания. Однако, если и удалось бы получить точные аналитические зависимости, то по аналогии с циклическим обслужи­ванием вычисления по этим формулам были бы весьма громоздкими и трудоемкими и были бы' связаны с использованием ЭВМ. При этом практически полностью терялись бы основные преимущества аналитического исследования по сравнению со статистическим моде­лированием. Поэтому более целесообразно проводить исследование таких систем в два этапа. Первый этап связан с получением при­ближенных аналитических зависимостей, на основе которых могут быть оценены основные характеристики обслуживания и выбрано конкретное расписание. На втором этапе проводится исследование системы на статистической модели при различных предположениях о характере потоков и обслуживания заявок. В отношении времени ожидания можно предположить, что его значение для каждого класса заявок h будет обратно пропорционально вероятности обра­щения к очереди данного класса: _h~1/_h, т. е. с уменьшением вероятности _h время ожидания заявок класса h увеличивается. Однако это совсем не означает, что заявки класса с меньшей вероятностью обращения всегда будут иметь большее время ожида­ния. Исследования показали, что время ожидания заявок различ­ных классов в большей степени зависит от соотношений между параметрами потоков и механизма обслуживания разнотипных заявок, т. е. заявки, принадлежащие классу с большей вероят­ностью обращения, в некоторых случаях могут иметь среднее время ожидания, превышающее время ожидания заявок класса с меньшей вероятностью обращения.

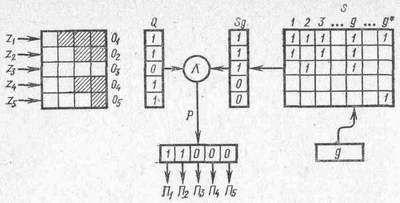
Рис. 3.26. Организация обслуживания заявок на основе расписания

Реализация обслуживания по расписанию. Обслуживание заявок на основе расписания организуется по схеме, показанной на рис. 3.26. Заявки z₁, ..., z₅, относящиеся к классам 1, ..., 5, ожидают обслуживания в очередях О₁, ..., О₅. С целью сокращения непроизводительных затрат на просмотр пустых очередей используется слово состояния очередей Q. Разряды q_l, ..., q₅ слова Q принимают значения q_i=0, если очередь Oi пуста; qi=1, если очередь O_i не пуста. Расписание представляется булевой матрицей S. В данном слу­чае строки матрицы соответствуют классам h=l,...,5 заявок, а столбцы — подциклам расписания. Подцикл, управляющий обслужи­ванием заявок, выделяется счетчиком g. В начальном состоянии g=l и затем значение g изменяется в циклическом порядке: g=l,2,..., g*, 1, 2, ..., g*, 1, 2, ... .

Управляющая программа функционирует следующим образом.

1. Из матрицы расписания S выбирается столбец S_g, выделя­емый текущим значением счетчика g. Столбец Sg представляется двоичным словом.

2. Слова Q и S_g умножаются поразрядно. В результате фор­мируется слово P=Q^S_g, разряды которого определяют не пустые очереди, обрабатываемые в подцикле g.

3. Управляющая программа последовательно просматривает раз­ряды i=l, 2, ..., 5 слова Р. Если i-й разряд слова равен 1, то инициируется программа П_i, которая начинает обрабатывать все заявки из очереди O_i, после чего управление вновь передается управляющей программе и просматривается очередной разряд слова Р.

4. После просмотра всех разрядов слова Р значение счетчика циклически увеличивается на единицу и выполняется переход к пункту 1.

Управление по расписанию целесообразно применять в системах с большой интенсивностью потока заявок — порядка 1·10² с^-1 и более — и широким диапазоном ограничений на времена ожидания заявок. В этом случае затраты процессорного времени на диспетчирование вполне измеримы и многочисленность вариантов распреде­ления единиц в матрице расписания позволяет подобрать такое управление порядком обслуживания, при котором фактические вре­мена ожидания хорошо приближаются к требуемым.