Модели вычислительных систем как систем массового обслуживания

1 Общие понятия и определения

Анализ и синтез систем, функционирование которых описывается в рамках терминов "состояние — переход из состояния в состояние", возможен методами теории массового обслуживания В теории массового обслужи-вания основным предметом исследования является система массового обслуживания.

Система массового обслуживания (СМО) — это динамический объект (система), в котором выполняется последовательность операций по обслуживанию потока заявок. Система может осуществлять конечное число операций различного типа. Элементы системы, в которых реализуются операции, называются обслуживающими приборами (каналом) или просто прибором.

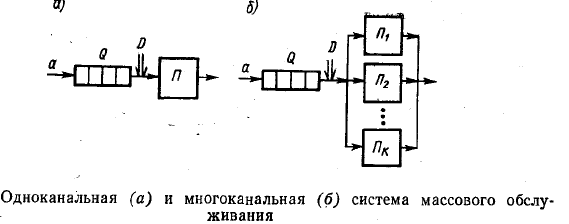
В теории массового обслуживания физическая и алгоритмическая сущность операций игнорируется.

Обобщенная структурная схема СМО приведена на рис. 1.

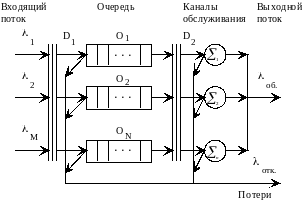
Рисунок 1 - Обобщенная структура системы массового обслуживания

• СМО обозначаются как X/Y/k

X,Y-законы распределения длительности интервала между заявками и интервала обслуживания,

M-экспоненциальный , G-произвольный

k-число обслуживающих устройств

Например m/m/1

Всякая СМО предназначена для обслуживания какого-то потока заявок, поступающих в какие-то случайные моменты времени. Заявки могут быть внешними и внутренними. Внешние заявки поступают извне системы, как правило, однородные (т.е. требующие однородного обслуживания). В зависимости от порождающей их причины делятся на типы, интенсивность потока заявок типа i 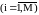обозначается как 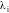. Совокупность входных заявок всех типов называется рабочей нагрузкой системы. Внутренние заявки могут возникать в момент окончания операции.

Обслуживание заявок выполняется совокупностью n в общем случае разнотипных каналов (приборов) K и продолжается случайное время 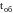. Функция распределения времени обслуживания как и интервала времени между заявками считается известной.

Случайный характер потока заявок и времен обслужи-вания приводит к тому, что в какие-то периоды времени на входе СМО накапливается излишне большое число заявок. Они либо становятся в очередь 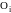с числом мест 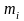либо покидают СМО необслуженными образуя поток отказов интенсивностью 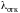. В другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Состояние СМО меняется скачком в моменты появления каких-то событий (или прихода новой заявки, или окончания обслуживания заявки, или в момент, когда заявка, которая не может больше ждать, покидает очередь).

Основная задача теории массового обслуживания — построение математических моделей, связывающих заданные параметры СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас показателями эффективности СМО, описывающими с той или другой точки зрения ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от цели исследования) могут применяться разные параметры, например, среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение и т.д.

Математический анализ работы СМО значительно облегчается, если процессы, протекающие в ней будут марковскими. Мы уже знаем , что для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние (потоки заявок, потоки "обслуживаний") были простейшими. Если это свойство нарушается, то математическое описание процесса становится гораздо сложнее и довести его до явных аналитических формул удается лишь в редких случаях. Однако аппарат простейшей марковской теории массового обслуживания может пригодиться для приближенного описания работы СМО даже в тех случаях, когда потоки событий — не простейшие [20]. Во многих случаях для принятия разумного решения по организации работы СМО вовсе и не требуется точного знания всех ее характеристик — зачастую достаточно и приближенного, ориентировочного.

Системы массового обслуживания делятся на типы (или классы) по ряду признаков. Первое деление: СМО с отказами и СМО с очередью.

В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе не участвует.

В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, становится в очередь и ожидает возможности быть обслуженной. На практике чаще встречаются СМО с очередью; недаром теория массового обслуживания имеет второе название "теория очередей".

СМО с очередью подразделяется на разные виды, в зависимости от того, как организована очередь — ограничена она или нет. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые "СМО с нетерпеливыми заявками").

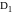Процесс продвижения заявки от входа к выходу СМО происходит с некоторым законом управления процессами в СМО, который задается дисциплинами ожидания ( ) и обслуживания ( ).

Дисциплина ожидания определяет порядок приема заявок в систему и размещения их в очереди.

Дисциплина обслуживания определяет порядок выбора заявок из очереди для назначения их на обслуживание.

Если по каким-либо причинам заявки некоторых типов должны обслуживаться быстрее, то они получают преимущество перед заявками других типов, называемое приоритетом. Приоритеты заявок характеризуются положительными числами 1, 2, 3, ..., причем более высокому приоритету соответствует меньшее число. Различают относительный и абсолютный приоритеты.

Относительный приоритет учитывается только в момент назначения заявки на обслуживание. При освобождении канала обслуживания сравниваются приоритеты заявок, находящихся в очереди в состоянии ожидания, и обслуживание предоставляется заявке с наибольшим приоритетом.

Абсолютные приоритеты предполагают прерывание обслуживания низкоприоритетной заявки в момент поступления в СМО заявки с более высоким приоритетом, прерванная заявка ставится в начало либо общей очереди, либо очереди заявок соответствующего приоритета.

Кроме этих признаков, СМО можно разделить на: "открытые" и "замкнутые". В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии находится сама СМО (сколько каналов занято). В замкнутой СМО — зависят: очередная заявка поступает в СМО только после завершения полного обслуживания одной из предыдущих заявок. Поэтому в замкнутой СМО количество заявок постоянно и равно тому числу, которое может одновременно обслуживать СМО. Классификация СМО далеко не ограничивается приведенными их разновидностями, но мы ограничимся ими.

Оптимизация работы СМО может производиться под разными углами зрения: с точки зрения администраторов (или владельцев) СМО или с точки зрения обслуживаемых клиентов. С первой точки зрения желательно "выжать все, что можно" из СМО и добиться того, чтобы все ее каналы были предельно загружены. С точки зрения клиентов желательно всемерное уменьшение очереди. При решении задач оптимизации в теории массового обслуживания существенно необходим системный подход, полное и комплексное рассмотрение всех последствий каждого решения. Например, с точки зрения клиентов СМО желательно увеличение числа каналов обслуживания; но ведь работу каждого канала надо оплатить, что удорожит обслуживание. Построение математической модели позволяет решить оптимизационную задачу о разумном числе каналов с учетом всех "за" и "против". Поэтому не выделяется в задачах массового обслуживания какой-либо один показатель эффективности, а сразу ставятся эти задачи как многокритериальные.

Совокупность взаимодействующих СМО, в среде которых циркулируют заявки, — это сети массового обслуживания или стохастические сети.

Если в сети существуют внешние источники заявок, то такая сеть называется открытой. В противном случае сеть будет замкнутой. В замкнутой сети общее число заявок фиксировано и постоянно. Два простых примера открытой и замкнутой сети представлены на рис. 4.2.

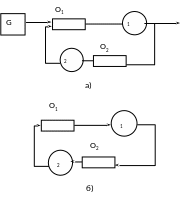
Рисунок .2 - Сети массового обслуживания: а) открытая; б) замкнутая