1. Анализ надежности кс со сложной структурой

 

Расчет надежностных характеристик УВКС. Расчеты проведены, исхо­дя из требований по надежности, предъявленных к комплексу, для нескольких неизбыточных и избыточных конфигураций УВКС по следу­ющим стандартным формулам для последовательных и параллельных

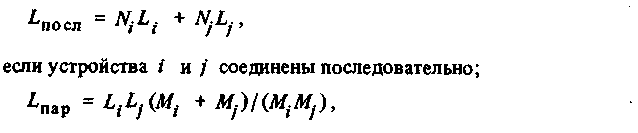
если устройства i и j соединены параллельно.

В формулах приняты следующие обозначения: N_i, N_j,- ~ число уст­ройств типов i и j соответственно; L _i l_j - интенсивности отказов устройств соответствующих типов; M_i M_j - интенсивности восстанов­ления после отказа устройств соответствующих типов; L_посл и L_пар -интенсивность отказов блока, состоящего из последовательно или парал­лельно соединенных устройств соответственно.

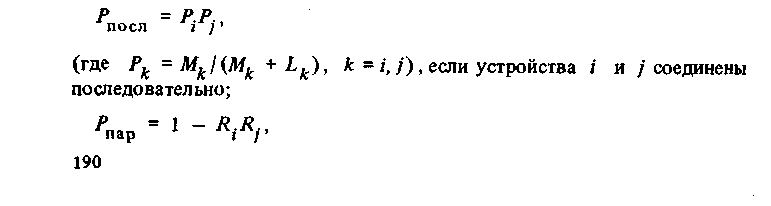Интенсивность отказов L всего комплекса равна сумме всех L_посл и L_пар блоков устройств, входящих в рассматриваемую конфигурацию комплекса. Среднее время наработки на отказ всего комплекса опреде­ляется по формуле

Интенсивность отказов L всего комплекса равна сумме всех L_посл и L_nap блоков устройств, входящих в рассматриваемую конфигурацию комплекса. Среднее время наработки на отказ всего комплекса опреде­ляется по формуле

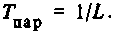
Графо-аналитический метод расчета надежности КС

Определить надежность системы, если надежности узлов, обозначенные на рисунке, даны: Р₁ = 0,9; Р₂ = 0,8.

P₁ = 0,9

P₂ = 0,8

P_CD = P₁ ; P_KL = 1 - (1 - P₁)(1-P₂) ;

P_AB = P₁ P₂ ; P_MN = 1 - (1 - P_CD) (1 - P_AB);

P_ML = P_MN ∙P_KL = (1 - (1 - P_CD) ∙ (1 - P_AB)) ∙ (1 - (1 - P₂) (1-P₂) )=

(1 - (1 - P₁) ∙ (1 - P₁∙P₂)) ∙ (1 - (1 - P₂) (1-P₂)) =

(1 - 0,1 ∙ 0,28) ∙ (1 - 0,2²) = (1 - 0,028) ∙ (1 - 0,04) = 0,972 ∙ 0,96 = = 0,993

2.Расчет надежности кс

Пусть задана система следующей конфигурации:

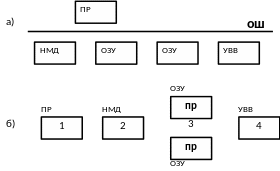
λ_i, λ_j - интенсивности отказов;

µ_i, µ_j - интенсивности восстановления.

а) структура

б) схема расчета надежности

λ_посл = n_i λ_i + n_i λ_i (устройства соединены последовательно)

λ_пар = λ_i λ_j (µ_i + µ_j) / µ_i µ_j (устройства соединены параллельно)

где: n_i, n_j - число устройств i и j

λ_i, λ_j - интенсивности отказов

µ_i, µ_i - интенсивности восстановления

Интенсивность отказов всего комплекса:

λ = ∑ λ_посл + ∑ λ_пар

Среднее время наработки на отказ:

Т = 1 / λ

Коэффициент готовности:

К = Р_i ∙ Р_j , где Р_k = µ_k / (µ_k + λ_k); k = i, j

Модели оценки трудоемкости алгоритма.

Трудоемкость алгоритма – количество вычислительной работы, требуемой для реализации алгоритма.

В задачах оценки трудоемкости операторы алгоритма разделяют на функциональные, перехода и ввода-вывода.

Функциональный оператор задает преобразование на множестве данных, т.е. задает некоторую совокупность вычислительных операций.

Оператор перехода задает порядок вычисления функциональных операторов и правило выбора одного из возможных путей развития вычислительного процесса, соответствующего текущим значениям данных.

Оператор ввода-вывода задает обращение к определенному файлу с целью передачи некоторого количества информации.

Функциональные операторы и операторы перехода называют основными операторами.

Совокупность операторов и связей между ними наиболее наглядно представляется графом алгоритма, где вершины соответствуют основным операторам алгоритма, а дуги отображают связи между операторами.

Вершины графа бывают трех типов: начальная, конечная и операторная.

Начальная вершина определяет начало алгоритма. Эта вершина не имеет ни одного входа и имеет только один выход. Конечная вершина определяет конец алгоритма и имеет не менее одного входа и ни одного выхода.

Операторная вершина соответствует основному оператору или оператору ввода-вывода. Если она представляет функциональный оператор или ввода-вывода, то может иметь не меньше одного входа и только один выход. Если она представляет оператор перехода, то может иметь не меньше одного входа и не меньше двух выходов.

Граф алгоритма является корректным, если выполняются условия:

- имеется только одна начальная и только одна конечная вершина;

- для каждой вершины кроме начальной существует по крайней мере один путь, ведущий в эту вершину из начальной;

- из каждой вершины кроме конечной существует по крайней мере один путь, ведущий из этой вершины в конечную;

- выход из любой вершины должен вести только к одной вершине графа;

- при любых значениях логических условий существует путь из начальной вершины в конечную, причем любому фиксированному набору значений условий соответствует только один такой путь.

Пример графа алгоритма приведен на рисунке 1.

Рисунок 1 — Пример представления графа алгоритма

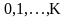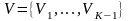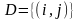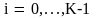Вершины графа обозначены номерами ; (0 - начальная вершина, K - конечная; 1,...,K-1 идентифицируют операторы алгоритма). Граф выявляет структуру алгоритма, определяя множество операторов и дуг , и 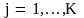, связывающих операторы.

Порядок расчета трудоемкости алгоритмов.

Для расчета алгоритма, не содержащего циклы, необходимо:

1. пронумеровать вершины графа в порядке их следования следующим образом: начальной вершине присваивается номер 0; очередно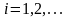й номер присваивается вершине, в которую входят дуги от уже пронумерованных вершин с номерами, меньшими . Конечная вершина графа будет иметь максимальный номер .
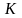