Напряженность электрического поля и распределение потенциалов в резком p-n переходе5

Резкий p-n переход – такой переход, у которого на границе раздела pи nобластей 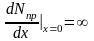. Так как концентрация примеси в p-n переходе меняется лишь по одному направлению, то внутреннее электрическое поле внутри p-n перехода также меняется лишь по одной координате и отсутствует в других направлениях, то есть при анализе можно ограничиться одномерным случаем. (см. рис.)

Так как объёмные заряды в p-n переходе образуются за счёт диффузионного разделения зарядов ранее скомпенсированных, то в целом p-n переход как изолированная система остаётся электронейтральным. Поэтому заряд отрицательных ионов, нескомпенсированных в p-области, равен заряду положительных ионов нескомпенсированных доноров в n-области, то есть 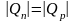. Для резкого p-nперехода заряд ,

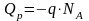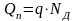
Величина электрического поля, создаваемого этими зарядами определяется из уравнения Пуассона:

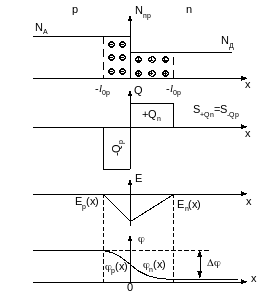
Рис. Напряженность электрического поля и распределение потенциалов в резком p-nпереходе

.

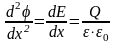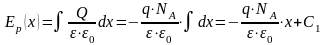
При 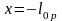- нескомпенсированных зарядов нет, тогд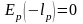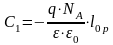а , . Отсюда 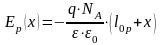при .

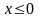Аналогично можно получить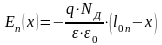 при 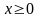. «-» показывает, что при выбранном направлении координаты «x» вектор напряжённости 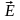направлен навстречу «x».

E – максимально на границе раздела p-n областей.

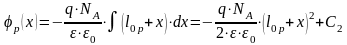
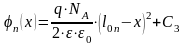
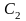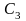Постоянные интегрирования и определяются следующими условиями. Для того, чтобы электрон перешёл из n-области в p-область, ему надо преодолеть силы электрического поля. Поэтому если потенциал рассчитывается для отрицательных частиц (электронов), то потенциал p- области будет выше потенциала n-области на величину . Потенциал изменяется только там, где имеются силы электрического поля. Следовательно, изменение потенциала наблюдается только в области объёмного заряда, а в глубине p-и n-областей потенциал постоянен. В полупроводниковой технике потенциал n-области обычно считается нулевым.

При : , .

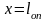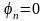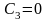При : , .

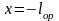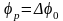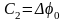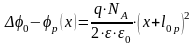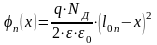при .

при .

То есть в пределах p-nперехода потенциал меняется по квадратичному закону с точкой перегиба 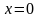. В глубине p- и n- областей потенциал постоянен.

Ширина области объёмного заряда резкого p-nперехода6

Из непрерывности электрического поля на границе p-n перехода получаем: 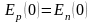, , 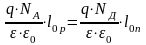тогда 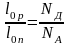. Полную ширину области объёмного заряда обозначим через . .

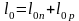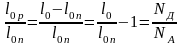, отсюда .

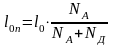Аналогично .

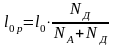Из условия непрерывности потенциала на границе p-n областей:

. .

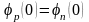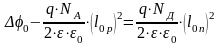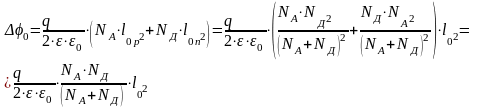
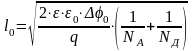
То есть ширина области объёмного заряда (часто её называют шириной обеднённой области p-nперехода, шириной запорного слоя p-n перехода, или просто шириной p-n перехода) определяется степенью легирования p-n областей.

Причём, чем больше степень легирования, тем уже область объёмного заряда. С уменьшением степени легирования, область объёмного заряда увеличивается. Связано это с тем, что область объёмного заряда создаётся неподвижныминескомпенсированными ионами примеси. Поэтому, чем больше степень легирования, тем меньше расстояние между ионами примеси, а большая плотность ионов определяет меньший объём, занимаемый зарядом Q, а, следовательно, и меньшее .

Обеднённая зона – мало подвижных носителей. Запорный слой – поле против движения основных носителей.

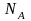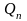Так как объёмные заряды в p- и n- областях равны, то в случае несимметричного p-n перехода, то есть с резким отличием концентраций носителей, а значит и , равные заряды и 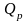будут занимать разные объёмы.

Например, , тогда .

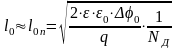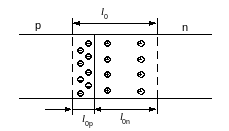
Рис. Ширина несимметричного p-nперехода

То есть в несимметричном p-n переходе ширина области объёмного заряда в основном определяется шириной высокоомной области. в зависимости от степени легирования может быть от сотых долей до десятков мкм. В современных полупроводниковых приборах и схемах обычно сравнима с толщиной p- и n- областей.