Лекция № 4-5

Содержание по учебному плану:Контактные явления в полупроводниках. Электронно-дырочный переход. Равновесное состояние p-n перехода. Контактная разность потенциалов. Ширина области объемного заряда. Прямое и обратное смещение р-n перехода.Граничные концентрации носителей в р-n переходе. Инжекция и экстракция носителей. Распределение концентраций неравновесных носителей в р- и n- областях перехода.

Электронно-дырочный переход

Электронно-дырочным переходом или просто р—n-переходом называют контакт двух полупроводников с различным типом проводимости, осуществленный в едином монокристалле полупроводникового материала. Р—n-переходы являются основой большого класса полупроводниковых приборов, применяемых для преобразования и усиления электрических сигналов.

При анализе работы полупроводниковых приборов удобнее измерять энергию не в электронвольтах, а в единицах потенциала — вольтах. Численно эти величины одинаковы. Чтобы перейти от одной размерности к другой, достаточно разделить энергию Еи kTна элементарный заряд q¹:

,

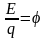где 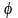— потенциал, характеризующий энергию. Величину

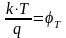
называют температурным потенциалом. При Т=300 К 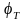=0,025 В. При замене Е на все приведенные ранее уравнения не изменяют своего смысла.

Равновесное состояние p—n-перехода2

Предположим, что концентрация равновесных носителей в изолированных р- и n-областях, из которых формируется р—n-переход, соответствует рис. 2.1,а. Зонные диаграммы этих областей показаны на рис. 2.1,б. Положение уровня Ферми в каждой изолированной области определяется кон­центрацией равновесных основных носителей уравнениями (1.12) и (1.13).

Если осуществить контакт этих областей в едином моно­кристалле полупроводникового материала, т. е. сформиро­вать р—n-переход (рис. 2.2,а), то вследствие градиента кон­центрации однотипных носителей в пограничном слое начнет­ся их диффузионное движение из одной области в другую. Так как концентрация дырок в области р значительно боль­ше, чем в области п, то дырки диффундируют из р-области в область п. По той же причине электроны стремятся перей­ти из n-области в область р.

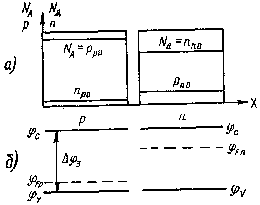
Рис. 2.1. Концентрация носителей в изолиро­ванных р- и n-областях (a)и зонные диаграм­мы изолированных областей (б)

Рис. 2.2. Структура (а) и зонные диаграммы (б) р—n -перехода в равновесном состоянии

Диффузия основных носителей нарушает в пограничных слоях равновесную компенсацию зарядов неподвижных ионов примеси зарядами подвижных носителей, и на границе р- и n-областей образуется двойная область объемного заряда, обусловленная отрицательными ионами акцепторов в обла­сти р и положительными ионами донорной примеси в области n (рис. 2.2,а). Объемный заряд приводит к появлению в приконтактной области электрического поля Е, которое пре­пятствует дальнейшей диффузии основных носителей и одно­временно вызывает встречный дрейфовый поток неосновных носителей. При равновесном состоянии р—n-перехода, в от­сутствие внешнего напряжения, дрейфовый поток в точности компенсирует диффузионный поток носителей, и суммарный ток через переход равен нулю (рис. 2.2).

Под действием сил электрического поля в области объем­ного заряда р—n -перехода происходит искривление энергети­ческих зон (рис. 2.2,б), что способствует установлению об­щего уровня Ферми для всего перехода в целом. Положение уровня Ферми в любой системе, находящейся в равновесном состоянии, должно быть одина­ковым. В результате искривления электрическим полем энер­гетических зон на границе раздела р- и n -областей появля­ется потенциальный барьер, высота которого характеризу­ется контактной разностью потенциалов (рис. 2.2,б).

Из сравнения рис. 2.1,б и 2.2,б следует, что величина контактной разности потенциалов равна разности положе­ний уровней Ферми в исходных полупроводниках n- и р – типа:

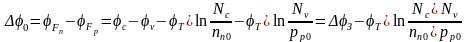(2.1)

Из закона действующих масс для области п следует:

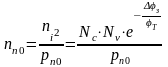
Подставляя это значение п_п0в уравнение (2.1), получаем³

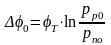
Если применить закон действующих масс для области р, то получим аналогичное уравнение:

. (2.2)

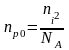То есть высота потенциального барьера р—n-перехода в равно­весном состоянии определяется соотношением концентрации однотипных носителей на границе перехода. Следовательно, зависит от степени легирования р- иn-областей. Напри­мер, повышение степени легирования приводит к увеличению концентрации основных носителей (например, в области п) и к уменьшению концентрации неосновных носителей( в области р), вследствие чего возрастает.

Предельную величину можно определить из (2.1), учитывая, что при не очень низких температурах 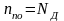, 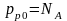.Тогда

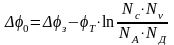(2.3)

При 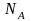,  см^-3 , т.е. стремится к ширине запрещенной зоны. Это является следствием того, что с повышением степени легирования уровни Ферми в р- и n-областях приближаются к краям соответствующих зон. Следовательно, для Ge В, для Si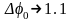 В и т. д. В реальных переходах с более низкой степенью легирования имеет меньшую величину⁴. Однако при прочих равных условиях больше в том переходе, который изготовлениз материала с большей шириной запрещенной зоны .Этотвывод непосредственно следует из (2.3).

Из (2.3) также следует, что с ростом температуры уменьшается примерно по линейному закону. Это объясняет­ся тем, что с увеличением температуры концентрация основных носителей меняется слабо, а концентрация неосновных носителей растет по экспоненциальному закону. При высо­ких температурах, близких к критической температуре полу­проводника, примесные полупроводники превращаются в собственные, уровни Ферми в р- и n- областях сравниваются, 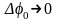, переход исчезает.

В равновесном состоянии кристалл р—nперехода в целом электрически нейтрален. Поэтому суммарный заряд нескомпенсированных отрицательных ионов акцепторов в области объемного заряда равен суммарному заряду нескомпенсированных положительных ионов доноров. Ширина области объ­емного заряда (Часто ее называют просто шириной р—n-пе­рехода) определяется степенью легирования р- и n-областей. Причем, чем больше степень легирования, тем уже область объемного заряда. Это связано с тем, что эта область созда­ется неподвижными ионами примеси. Поэтому, чем больше концентрация примеси, тем меньше расстояние между ато­мами, а следовательно, и между ионами примеси. Большая плотность ионов определяет меньший объем, занимаемый зарядом. В равновесном состоянии ширина перехода обозна­чается через .

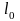Для переходов со ступенчатым изменением концентрации примеси на границе раздела р- и n-областей (такие перехо­ды называют резкими р—n-переходами) ширина области объемного заряда в равновесном состоянии определяется уравнением

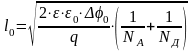(2.4.а)

Если переход характеризуется плавным распределением примеси, например линейным,

,

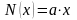то ширина области объемного заряда определяется урав­нением

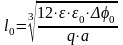. (2.4,б)

В несимметричных переходах с резко различной концен­трацией примеси равные заряды нескомпенсированных ионов примеси в р- и n- областях будут занимать соответственно различные объемы. Если например, 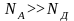, то

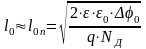
т. е. в несимметричном переходе ширина р—n- перехода опре­деляется в основном протяженностью той области, степень легирования которой меньше.