5.8. Принцип работы лазеров

► Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна. Рассмотрим атом, находящийся в поле равновесного из­лучения. Если атом находится в состоянии с энергией , то под воздей­ствием излучения он может перейти в состояние с большей энергией , поглотив при этом световой квант с частотой (рис.95). Такой процесс называют вынужденным (индуцированным) поглощени­ем. Вероятность такого перехода в единицу времени пропорциональна плотности энергии излучения на частоте ω:

Обратный переход, из состояния с большей энергией в состояние с мень­шей энергией, связан с рождением и излучением кванта частоты ω. Он может происходить двумя способами. Первый тип переходов называ­ется спонтанным излучением, он происходит и в отсутствие внешнего излучения (при и_ω = 0), и его вероятность от и_ω не зависит

Второй тип переходов называется вынужденным излучением, он про­исходит под воздействием кванта частоты ω. Вероятность перехода в единицу времени, как и для вынужденного поглощения, пропорци­ональна и_ω:

Введенные таким образом коэффициенты , , называются коэффициентами Эйнштейна, они не зависят от температуры излуче­ния.

► Равновесие между атомами и излучением. Пусть в объеме, заполненном равновесным излучением при температуре Т, находятся одинаковые атомы. Будем считать, что установилось тепловое равно­весие между атомами и излучением, при этом среднее число атомов в состоянии I равно N_i а в состоянии j равно N_j. Эти числа при температуре Т связаны между собой соотношением Больцмана:

.

В состоянии равновесия число переходов из i в j должно быть равно числу обратных переходов:

(39)

Из соотношения Больцмана следует, что при . Учитывая, что при этом , получаем, что . Выразим из (39) и_ω:

(40)

(мы учли, что . Видно, что мы фактически выве­ли формулу Планка для равновесного излучения. Отношение может быть получено из условия, что при высоких температурах дол­жна быть верна классическая формула Рэлея – Джинса:

.

Посмотрим на это соотношение с иной точки зрения. Учитывая (38) для числа квантов с определенной частотой, запишем (40) в виде

Следовательно, отношение вероятности вынужденного излучения к ве­роятности спонтанного излучения равно числу квантов частоты ω. Можно сказать иначе: вероятность вынужденного излучения в расчете на один квант равна вероятности спонтанного излучения. Видно, что спонтанное и вынужденное излучение должны быть одной природы.

Объяснение (качественное) состоит в том, что даже в отсутствие в си­стеме световых квантов в полости существуют так называемые нулевые колебания электромагнитного поля данной частоты (энергия осцилля­тора в квантовой механике равна ). Именно эти колебания и являются причиной спонтанных переходов.

► Инверсная заселенность уровней. В каждом акте вынужден­ного излучения происходит образование нового кванта, причем рож­денный квант имеет такую же фазу, как квант, вызвавший это излу­чение. Иначе говоря, вместо одного кванта в системе появляются два когерентных кванта. Каждый из этих квантов может в свою очередь вызвать появление нового когерентного кванта и т.д. Таким образом может происходить усиление когерентного излучения. Однако вновь рожденные кванты поглощаются атомами, находящимися в более низ­ком из двух энергетических состояний. В равновесном состоянии число атомов в нижнем состоянии (населенность нижнего уровня) выше, чем в верхнем. Следовательно, поглощение будет превалировать над вынужденным излучением, и усиление оказывается невозможным.

Для того чтобы усиление когерентного луча стало возможным, на­до создать метастабильное состояние, обладающее инверсной населен­ностью уровней. Тогда усиление потока квантов будет происходить по формуле

(41)

где , – концентрации атомов, – сечение вынужденного поглощения или излучения, – коэффициент квантового усиления среды.

Д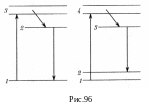 ля создания инверсной населенности используются различные методы накачки. Самыми распространенными являются трехуров­невые и четырехуров­невые схемы (рис.96). В трехуровневой схеме (рубиновый лазер) происходит интенсивная накачка с нижнего уровня 1 на широкий короткоживущий уровень 3, с которого происходит заполнение долгоживущего (метастабильного) уровня 2. Необходимо добиться, чтобы населенность верхнего рабочего уровня 2 превысила населенность нижнего рабочего уровня 1. Трудность состоит в том, что изначально населенность уровня 2 много меньше населенности

1 Законы фотоэффекта были открыты Столетовым.