5.6. Тепловое излучение

► Равновесное тепловое излучение. Излучение электромагнит­ной (лучистой) энергии телом за счет энергии хаотического (теп­лового) движения его молекул называется тепловым излучением. Свойства теплового излучения определяются материалом тела и его температурой. Если из любого материала сделать замкнутую по­лость и поддерживать температуру ее стенок постоянной, то система (стенка + излучение) придет в состояние термодинамического равнове­сия, и в объеме полости установится равновесное тепловое излучение. Важнейшая особенность равновесного излучения состоит в том, что его свойства полностью определяются температурой стенок и не зависят от их материала. Это утверждение является следствием второго начала термодинамики. Кроме того, равновесное излучение однородно и изо­тропно.

Основные характеристики как излучения с поверхности тела, так и излучения в объеме были введены в разд. 5.1. Излучение с по­верхности характеризуется энергетической яркостью В и энергетиче­ской светимостью R, равной количеству лучистой энергии, излученной с единицы поверхности за единицу времени по всем направлениям (т. е. в телесный угол 2π). Вводятся также спектральные разложения энер­гетической светимости например величины r называются излучательными способностями тела. Излучение в объ­еме характеризуется интенсивностью лучистого потока I и объемной плотностью лучистой энергии и, а также их спектральными разложе­ниями. В случае изотропного излучения они связаны соотношением и = 4πI / c. Освещенность Е определяется как полный лучистый поток через единичную площадку со всех направлений (из телесного угла 2π); в случае изотропного излучения выполняются соотношения

Спектральные плотности освещенности Е обозначим . Пе­ресчет от одной спектральной характеристики к другой обсуждается в разд. 5.1.

► Поглощательная способность. Закон Кирхгофа. Поглощательной способностью тела называется доля падающей лучистой энер­гии, поглощенная телом (для узкого интервала длин волн или частот):

Тело, для которого во всем спектральном интервале, называет­ся абсолютно черным телом. Моделью черного тела может служить замкнутая полость с небольшим отверстием; почти все лучи, попадаю­щие в полость через отверстие, в результате многократных отражений от внутренних стенок оказываются поглощенными. Тело, у которого , называют серым.

Так как равновесное излучение находится в равновесии с поверхно­стью, то для любого спектрального интервала количество поглощенной лучистой энергии, равное , должно быть равно количеству излученной энергии, равному . Поскольку характеристики равно­весного объемного излучения не зависят от свойств конкретного тела, то отношение излучательной способности любого тела к его поглощательной способности оказывается универсальной функцией длины волны и температуры (закон Кирхгофа):

(21)

Поскольку для абсолютно черного тела поглощательная способность равна единице, то стоящая справа функция есть не что иное, как излучательная способность абсолютно черного тела, которую обозна­чим :

.

Видно, что излучательная способность абсолютно черного тела и его энергетическая светимость не зависят от способа его изготовления; они связаны с объемной плотностью энергии соотношениями

(22)

При одной и той же температуре абсолютно черное тело обладает самой большой излучательной способностью и энергетической светимостью. Например, для серого тела Отметим, что поскольку рав­новесное излучение изотропно, черное тело является ламбертовским источником (см. разд. 5.1).

► Законы Стефана — Больцмана и Вина. Излучательная спо­собность абсолютно черного тела при данной температуре стремится к пулю при малых и больших λ и достигает максимального значе­ния при некоторой длине волны λ_m, которая зависит от температу­ры. Площадь под кривой равна энергетической светимости R*(T). Применение к равновесному излучению в полости общих соотношений термодинамики позволило получить для него ряд общих соотноше­ний. (Температура равновесного теплового излучения считается равной температуре стенок.) Закон Стефана — Больцмана утверждает, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени температуры:

(23)

где — постоянная Стефана — Больцмана.

Для вывода (23) надо воспользоваться выражением для давле­ния изотропного излучения (см. разд. 2.5) и формулой , которая является следствием второго начала термодинамики (разд. 2.3). Подставляя , придем к уравнению , откуда получим . Кроме того, из формулы для давления и из первого начала термодинамики ( ) можно для равновесного излучения вывести уравнение адиабатического процесса: . Отсюда с учетом получим .

Если рассмотреть медленное адиабатическое изменение объема из­лучения, заключенного в сосуд с зеркальными стенками, и применить к отражению света от движущегося зеркала формулу эффекта Доплера (см. разд. 4.4, 4.5), то удается доказать формулу Вина:

или

(24)

где f_i(x) неизвестные функции, вид которых не может быть установ­лен в рамках термодинамики. Аналогичные выражения для имеют вид

или .

(25)

Из формулы Вина (24) (или (25)) можно вывести закон Стефана — Больцмана (2.3). Кроме того, из этих формул следует закон смещения Вина, выражающий зависимость положения максимума функции (или ) от температуры:

или ,

(26)

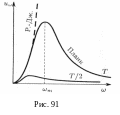
где - постоянная Вина. Например, при уменьшении температуры в два раза положение максимума функции (или ) становится в два раза ближе к началу координат, а сам максимум становится в восемь раз ниже (рис. 91); площадь под графиком уменьшается при этом в 16 раз.

► Формула Рэлея — Джинса. Рэлей и Джине предприняли по­пытку получить вид функции в рамках классической статисти­ческой физики. Они рассмотре­ли излучение в полости как ан­самбль стоячих электромагнитных волн, случайным образом обменивающихся энергией со стенками и между собой. С точки зрения ста­тистики, каждая независимая стоячая волна, имеющая некоторую частоту колебаний, эквивалентна осциллятору с такой же частотой. Вычисление энергии сводится к двум независимым вопросам:

1) Какое число dg осцилляторов (стоячих волн) приходится на интервал частот dω? Ответ должен выражаться в виде функции G(ω), которую называют плотностью состояний: , где V — объем сосуда.

Для вычисления G(ω) можно рассмотреть сосуд в форме прямоугольного параллелепипеда со сторонами L_x, L_y, L_z. Граничные условия (например, требование, чтобы на границах находились узлы стоячих волн) приводят к условиям . Следовательно, в пространстве волновых векторов допустимые состояния соответствуют узлам решетки со сторонами π / L_ξ и объемом ячейки . Объем k-пространства, соответствующий изменению величины волнового вектора от k до k + dk, равен (объем сферического слоя, отсекаемый первым квадрантом). Разделив на объем ячейки, получим число пространственно различных колебаний в интервале . Необходимо также учесть дополнительные степени свободы (в случае электромагнит­ных волн — два возможных состояния поляризации), которые для общности учтем дополнительным множителем γ.

Найдем число состояний на единицу объема:

(27)

Эта формула получена из граничных условий и имеет очень общий характер и многочисленные применения. Для перехода к ω надо учесть соотношение k = ω / c. Окончательно получим

(28)

2) Чему равна средняя энергия одного осциллятора?

Классическая физика дает следующий ответ (см. разд. 2.2): ка­ждому осциллятору, независимо от его частоты, надо приписать две степени свободы, и в соответствии с теоремой о равнораспределении энергии, средняя энергия каждого осциллятора должна быть равна kT, где k — постоянная Больцмана.

В результате таких рассуждений классическая физика приводит к формуле Рэлея – Джинса:

(29)

Опыт показывает, что формула Рэлея – Джинса хорошо выполняется на малых частотах (при ω << ω_m), но абсолютно неверна на больших (рис. 91). Действительно, хотя (29) удовлетворяет требованиям, нала­гаемым на любую возможную функцию и_ω формулой Вина (25), но сразу видно, что полученная функция не имеет максимума; она моно­тонно возрастает, и интеграл т.е. полная энергия излучения, равен бесконечности! Эта ситуация стала одним из признаков глубокого кризиса классической физики и была названа современниками ультра­фиолетовой катастрофой.

►Формула Планка. Теорема о равнораспределении энергии являет­ся следствием того, что классическая энергия осциллятора, пропорцио­нальная квадрату его амплитуды, может принимать любые, в том числе очень маленькие значения. Согласно квантовой гипотезе Планка энер­гия осциллятора (отсчитываемая от минимального значения) может принимать только дискретные значения, кратные некоторой величине, зависящей от частоты осциллятора:

(30)

Для вычисления средней энергии можно использовать формулу Макс­велла Больцмана (см. разд. 2.5), согласно которой вероятность состо­яния с энергией ε пропорциональна exp[-ε / (kT)]. Получаем

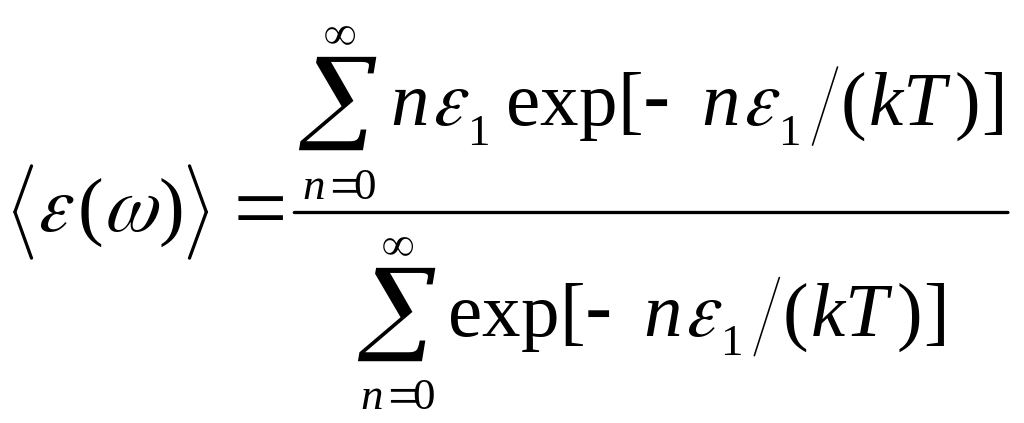
Ряд в знаменателе есть просто сумма геометрической прогрессии, а чис­литель получается из знаменателя дифференцированием по 1/(kT) Проведя вычисления, имеем

,

(31)

Сравнение с формулой Вина (25) показывает, что должна быть пропорциональна ω:

(32)

где — универсальная постоянная. Постоянную называют постоянной Планка, также называют посто­янной Планка или иногда просто «аш с чертой»; первую удобно исполь­зовать с частотой, а вторую с циклической частотой: . Так как энергия кванта пропорциональна частоте осциллятора, то при данной температуре колебания высоких частот возбуждаются с очень малой вероятностью и их вклад в энергию излучения оказывается ничтожно малым. Это разрешает проблему ультрафиолетовой ката­строфы.

После подстановки (32) в формулу для средней энергии получим формулу Планка для спектральной плотности энергии:

(33)

График этой функции приведен на рис. 91. Запишем формулу Планка также в переменных ν и λ:

,

(34)

При hω << kT формула Планка переходит в формулу Рэлея – Джин­са (29). Из формулы Планка можно получить выражения для постоян­ных Стефана – Больцмана и Вина через универсальные постоянные:

,

Формула Планка очень хорошо согласуется с экспериментом во всем диапазоне частот.