2.2. Понятия бесконечно малой и бесконечно большой функций. Ограниченная функция.

Определение. Функция называется бесконечно малой при , если .

Совершенно аналогично определяется бесконечно малая при , , , .

Пример 2.5.

а)  бесконечно малая при , поскольку .

б)  бесконечно малая при , т.к. .

Пусть определена в некоторой окрестности точки , кроме, возможно, самой точки .

Определение. Функция называется бесконечно большой при , если для любого, сколь угодно большого, числа найдётся такое, зависящее от , число , что для всех , удовлетворяющих условиям , выполняется неравенство (что означает либо , либо ).

Такой факт записывается в форме

(2.9)

Если при всех указанных выше условиях принимает только положительные значения, то пишут

(2.10)

если же только отрицательные, то

(2.11)

Подчеркнём, что равенства (2.9)  (2.11), хотя и содержат символ « », означают, что при предела не имеет, но является бесконечно большой.

Пример 2.6.

а)  бесконечно большая при х  1, т.е. .

б)  бесконечно большая при х  2, причём .

На рисунке 2.5. представлены графические интерпретации понятия бесконечно большой функции.

Бесконечно большая функция при , , , определяется аналогично. Используя математические обозначения, можно к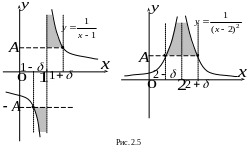 ратко записать :

, ,

, ,

(2.12)

Читателю предлагается самому дать графическую интерпретацию для каждого из этих вариантов.

Пример 2.7.

а) , , .

б) , , .

Определение. Функция называется ограниченной в заданной области изменения аргумента , если существует число , такое, что

при всех (2.13)

Определение. Функция называется ограниченной при , если существует окрестность, содержащая точку , в которой данная функция ограничена. Точно так же называется ограниченной при , , , , если существует правая полуокрестность точки (соответственно, левая полуокрестность , интервал , интервал ,  некоторое число), где данная функция ограничена.

Пример 2.8.

а)  ограничена во всей области определения , поскольку для .

б)  ограничена на всей числовой прямой.

в)  ограничена на любом интервале , где .

В дальнейшем будем использовать общее обозначение , подразумевая при этом один из вариантов: , , , , , . Под окрестностью точки будем понимать, соответственно, окрестность , правую или левую полуокрестность , интервал , , или же объединение интервалов .

Свойство бесконечно малых и бесконечно больших функций.

1. Если функция представляется в виде суммы числа и функции , бесконечно малой при , т.е. , то тогда .

И обратно, если , то можно представить в виде суммы: , где  бесконечно малая при .

2. Если является бесконечно малой функцией при и не обращается в ноль в некоторой окрестности точки , то тогда функция  бесконечно большая при .

И наоборот, если  бесконечно большая при , то  бесконечно малая при .

Например, при , при .

3. Пусть при  бесконечно малая, а  ограниченная функция. Тогда их произведение есть бесконечно малая функция при .

Пример 2.9. Вычислить предел .

Решение:  бесконечно малая при ,

 ограничена на , а значит и при .

Следовательно,  тоже бесконечно малая при , т.е. искомый предел равен нулю.