2. Классическое определение вероятности

Возможность появления некоторых случайных событий может быть измерена, т.к. каждое испытание (опыт) имеет какое-то количество результатов, т.е. – событий. Во многих случаях количество всех событий можно перечислить.

Мы уже говорили, что события, образующие полную группу попарно несовместимых и равновозможных событий называются элементарными событиями.

Определение (классическое определение вероятности): вероятностью P(A) события A называется отношение числа m элементарных событий, благоприятствующих событию A, к числу всех элементарных событий: .

Вероятность события имеет следующие свойства:

1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой U. Для достоверного события m=n, поэтому .

2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой V. Для невозможного события m=0, поэтому .

3. Вероятность случайного события выражается положительным числом, меньшим единицы ; т.к. .

4. Вероятность любого события B удовлетворяет неравенству: .

3. Геометрические вероятности

Классическое определение вероятности предполагает, что число всевозможных исходов – конечно. На практике часто приходится проводить испытания, в которых может происходить бесконечное количество исходов. В таких опытах для вычисления вероятности появления конкретного события классическое определение вероятности неприменимо и вводят геометрические вероятности – вероятности попадания точки в область.

Пусть на плоскости задана с помощью геометрического образа (отрезка, тела, фигуры) конкретная область, имеющая свою меру. Обозначим эту область буквой . В области содержится область . В области наудачу бросается точка. Будем считать, что брошенная точка может попасть в некоторую часть области с вероятностью, пропорциональной ее величине и независимой от ее формы и расположения. Пусть – попадание брошенной точки в область , тогда геометрическая вероятность этого события определяется формулой: , где – мера области ( – первые три буквы французского слова , что значит мера). Мера области может быть длинной ( ), площадью ( ), объемом ( ), где ( ) – длина, ( ) – площадь, ( ) – объем.

4. Алгебра событий

Определение 1: пространством элементарных событий называют произвольное множество , а его элементы – элементарными событиями.

Пусть – некоторая система случайных событий. Система случайных событий называется алгеброй событий, если выполняются условия:

1. ;

2. если и , то , , .

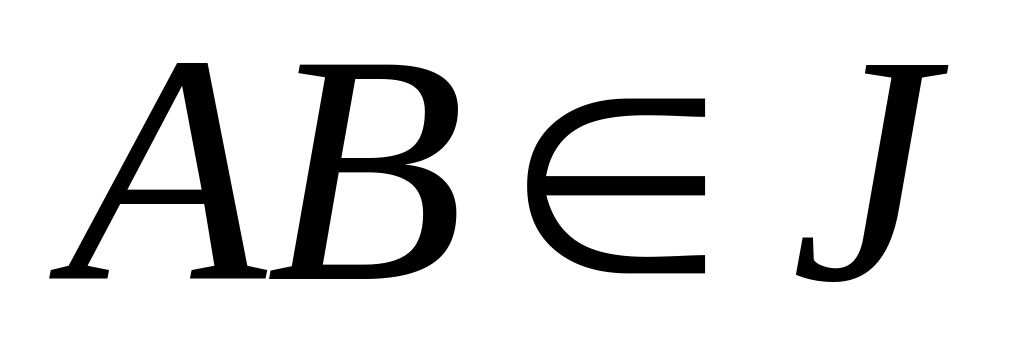Другими словам, система является алгеброй событий, если вместе с любыми двумя событиями она содержит их произведение, сумма и разность, а также множество . Из этих условий следует, что пустое множество также принадлежит .

Определение 2: Суммой или объединением событий А и В называется событие С=А+В, состоящее в наступлении хотя бы одного из событий А или В.

Пример: стреляют два стрелка и делают по одному выстрелу. Событие А – попадание в мишень первым стрелком; В – попадание в мишень вторым стрелком. Суммой С будет попадание в мишень хотя бы одним стрелком.

Заметим что, если есть событий то их суммой является хотя бы одно из событий .

Для событий справедливо , но , а не 2A.

Определение 3: произведением событий А и В называется такое событие , которое состоит в том, что в результате испытания произошло и событие А, и событие В.

В предыдущем примере о стрелках, произведением является попадание в мишень обоих стрелков.

Аналогично, что произведением конечного числа событий называется событие , состоящее в том, что в результате испытания произошли все указанные события. Из определения следует, что (а не ).

Определение 4: разностью событий А и В называется событие С, которое означает, что наступает событие А и не происходит событие В. Разность событий А и В обозначается или .

Числовая функция , определенная на алгебре событий , называется вероятностью, если выполняются следующие аксиомы:

1. Каждому событию ставится в соответствие неотрицательное число – его вероятность, т.е. для любого ( – свойство имеет место для каждого ).

2. Вероятность достоверного события равна единице.

3. Вероятность сумы двух несовместимых событий равна сумме вероятности этих событий.

4. Для любой убывающей последовательности событий из при .