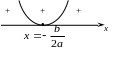- •Кафедра высшей и прикладной математики
- •Губкин 2009
- •Под редакцией в. В. Крутских
- •Справочный материал
- •1. Алгебра
- •1.1.Теория множеств
- •1.2. Действительные числа
- •1.3. Действия с дробями
- •1.4. Пропорция
- •1.5. Проценты
- •1.5. Погрешность вычислений
- •1.11. Определение логарифма
- •1.13. Свойства логарифмов
- •1.14. Логарифмирование и потенцирование
- •1.15. Теория многочленов
- •1.16. Выделение целой части из дроби
- •2. Алгебраические уравнения
- •2.1. Линейные уравнения
- •2.2. Квадратные уравнения
- •2.3. Выделение полного квадрата из квадратного трехчлена
- •2.4. Разложение квадратного трёхчлена на линейные множители
- •2.6. График квадратной функции
- •2.7. Рациональные уравнения
- •2.8. Уравнения с модулем
- •2.9. Кубические уравнения
- •2.9. Показательные уравнения
- •2.10. Логарифмические уравнения
- •3. Алгебраические неравенства
- •3.1. Линейные неравенства
- •3.2. Квадратные неравенства
- •Рациональные неравенства
- •3.5. Показательные неравенства
- •3.6. Логарифмические неравенства
- •3.7. Правила нахождения области определения и множества значений функции
- •4. Тригонометрия
- •5. Планиметрия
- •Треугольники
- •5.1. Косоугольный треугольник
- •5.3 Равнобедренный треугольник
- •Многоугольники
- •Четырехугольники
- •5.4. Параллелограмм
- •5.5. Прямоугольник
- •5.7. Квадрат
- •5.8. Трапеция
- •5.9. Окружность и круг
- •6. Стереометрия
- •Пирамида
- •Цилиндр
- •Сфера и шар
3.2. Квадратные неравенства
Квадратное
неравенство имеет вид
![]() (
(![]() ),
где
.
Решаем квадратное уравнение
),
где
.
Решаем квадратное уравнение
![]() и схематично изображаем график функции
относительно оси
.
Возможны случаи:
и схематично изображаем график функции
относительно оси
.
Возможны случаи:
1 |
2 случай. Уравнение имеет один корень |
3 случай. Уравнение не имеет корней |
|
|
|
Рисунок 3
При решении
неравенства
![]() штрихуем знак «+», а при решении неравенства
штрихуем знак «–».
штрихуем знак «+», а при решении неравенства
штрихуем знак «–».
Пример. Решить
неравенство: а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
► а)
Решим уравнение
![]()
![]()
![]()
![]()

Рисунок 4
![]() .
.
б)
решим
уравнение
![]()
![]() или
или
![]()

Рисунок 5
![]()
в)
![]()
![]()
![]()
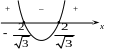

Рисунок 6
![]()
г)
Решим
квадратное уравнение
![]()
![]() ,
значит, квадратное уравнение корней не
имеет.
,
значит, квадратное уравнение корней не
имеет.
Рисунок 7
Неравенство верно
при любом![]() ◄
◄
Рациональные неравенства
Для решения рациональных и дробно-рациональных неравенств применяется метод интервалов.
Дробно-рациональное
неравенство имеет вид:
![]() (Если
знаменатель дроби содержит
,
то от знаменателя освобождаться нельзя!)
Числитель и знаменатель дроби нужно
разложить на множители вида
.
Обозначим
(Если
знаменатель дроби содержит
,
то от знаменателя освобождаться нельзя!)
Числитель и знаменатель дроби нужно
разложить на множители вида
.
Обозначим
![]() .
Находим:
.
Находим:
Нули
из условия:
![]()
Область определения
функции:
![]()
Полученные точки отмечаем на числовой прямой, расставим знаки левой части исходного неравенства на образовавшихся промежутках и запишем ответ.
Замечание.
Если левая часть неравенства содержит
четную степень скобки
![]() ,
то в точке
,
то в точке
![]() смены знака не происходит.
смены знака не происходит.
Пример. Решить
неравенство: а)
![]() б)
б)
![]()
►а) Отметим на числовой прямой точки, в которых левая часть неравенства обращается в нуль. Так как перед в каждой скобке стоит знак «+», то правый знак «+» и знаки чередуем, но переходя через точку знак не меняется.

Рисунок 8
![]()
б) Перенесем 2 в
левую часть и приведем выражение к
общему знаменателю.
![]()
![]()
![]()
![]()
Пусть
![]()
Нули
находим из условия:
![]()
![]()
Область определения
функции:
![]()
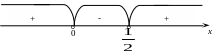
Рисунок 9
![]() ◄
◄
3.4. Иррациональные неравенства
I вид:
решений
нет, если
|
II вид:
|
III вид:
|
III вид:
|
Пример. Решить
неравенство: а)
![]() б)
б)
![]()
► а)
![]()
б)
![]()
![]() .
.
3.5. Показательные неравенства
I вид:
|
(16)
|
II вид:
|
(17)
|
III вид: введение новой переменной.
Пример. Решить
неравенства: а)
![]() б)
б)
![]() в)
в)
![]()
►а)![]() б)
б)
![]()
в)
![]() ◄
◄
3.6. Логарифмические неравенства
При решении логарифмических неравенств рекомендуется начинать с определения ОДЗ неравенства в системе, затем тщательно следить за равносильностью всех совершаемых преобразований.
I вид: |
|
(18) |
II вид: |
|
(19) |
II
вид: Преобразование неравенства к виду
![]() (Метод потенцирования).
(Метод потенцирования).
III вид: Введение новой переменной.
Замечание. При решении методом введения новой переменной для введенной переменной решение записываем в виде неравенств, и в эти неравенства выполняем обратную подстановку.
Пример. Решить
неравенства: а)
![]() б)
б)
![]()
в)
![]()
►а)![]()
![]()
![]()
![]()
![]()
в)
ОДЗ:
![]()
![]()
![]() По
свойству логарифмов 8, заменим
По
свойству логарифмов 8, заменим
![]() ,
получим:
,
получим:
![]() Решаем
методом подстановки
Решаем
методом подстановки
![]()
Получим неравенство
![]() Решаем дробно-линейное неравенство
методом интервалов.
Решаем дробно-линейное неравенство
методом интервалов.
![]()
![]()
![]()

Рисунок 10
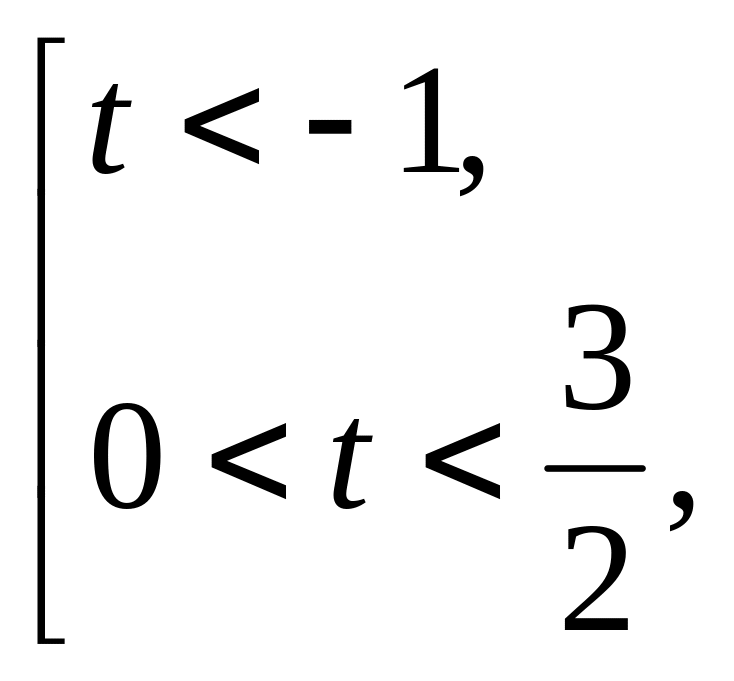
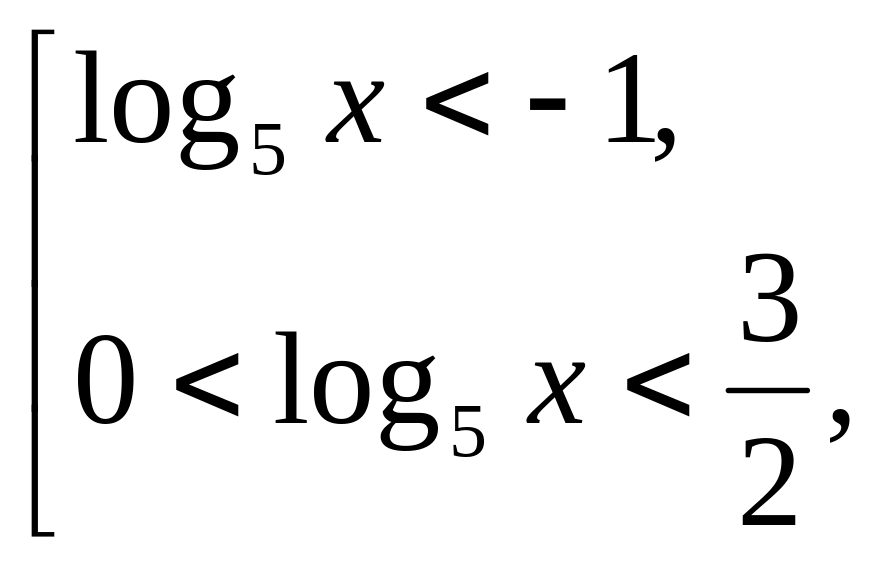
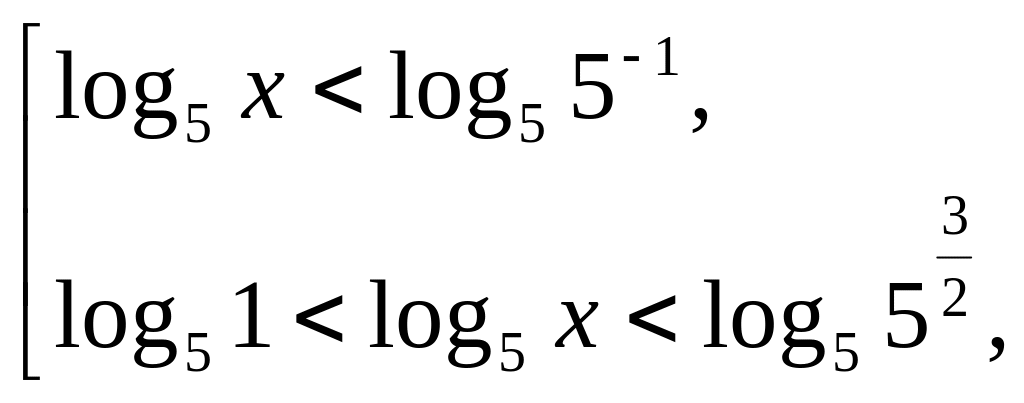
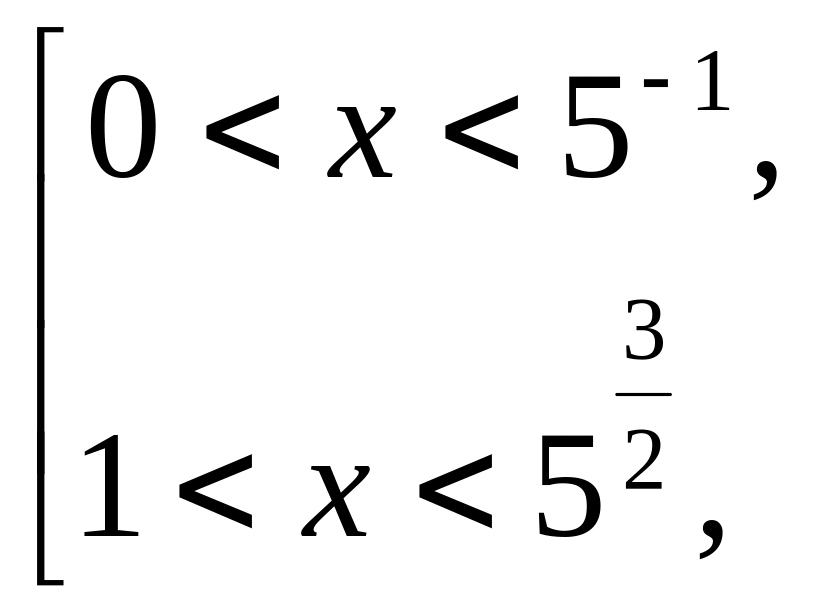
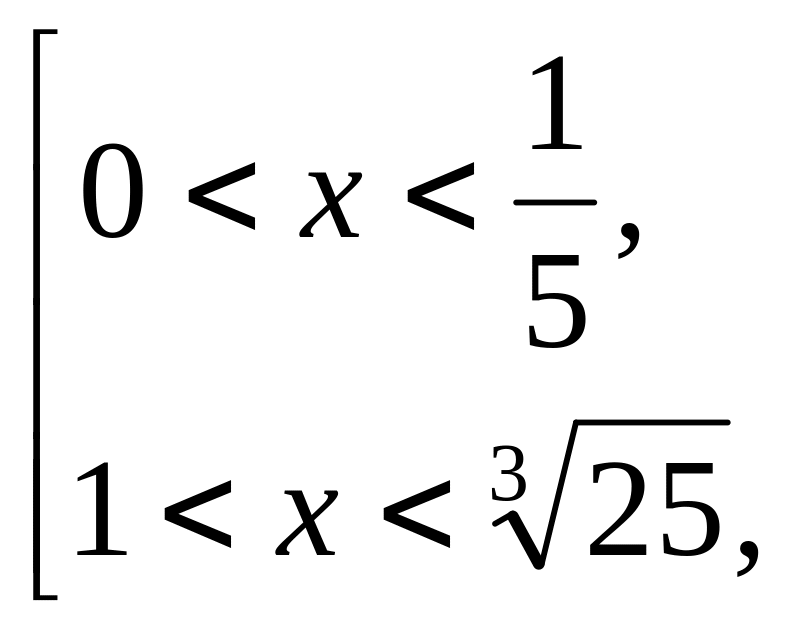
![]() ◄
◄

 случай. Уравнение имеет два корня
случай. Уравнение имеет два корня