2.1. Линейные уравнения

Линейное уравнение с одним неизвестным имеет вид:

(4)

1) если ,то

2) если , то есть то ;

3) если , то есть , то _.

Пример. Решить уравнение:

►ОДЗ .

Освободимся от знаменателя, умножив все слагаемые уравнения на 4

Перенесем члены уравнения, содержащие неизвестное, в левую часть уравнения, свободные члены - в правую:

.◄

2.2. Квадратные уравнения

Квадратным уравнением называется уравнение вида:

(5)

где заданные действительные числа, причём

Коэффициент при принято называть первым коэффициентом, коэффициент при — вторым коэффициентом, — свободным членом квадратного уравнения.

Если , то квадратное уравнение называется приведенным.

Выражение называется дискриминантом квадратного уравнения. В зависимости от знака дискриминанта возможны три случая:

а) при квадратное уравнение имеет два различных действительных корня:

б) при квадратное уравнение имеет два действительных равных корня:

в) при квадратное уравнение не имеет действительных корней.

Пример. Решить уравнение: а) б) в)

г) д) , е) .

►а)

,

б) это неполное квадратное уравнение, вынесем за скобки:

или

в) Неполное квадратное уравнение, выразим :

г) .

, .

д) ,

е) . действительных корней нет. ◄

2.3. Выделение полного квадрата из квадратного трехчлена

Квадратным трёхчленом называется функция вида

Выделим в этом трёхчлене полный квадрат. Прежде всего, вынесем за скобки коэффициент при :

Затем выражение представим в виде (удвоенное произведение числа на число ): , получим

Итак,

(6)

Пример. Выделить полный квадрат в трёхчленах: а) ;

б) .

►а)

◄

2.4. Разложение квадратного трёхчлена на линейные множители

Если и действительные корни квадратного трёхчлена, то его можно разложить на линейные множители с действительными коэффициентами:

(7)

Пример. Разложить на множители трёхчлен:

а) ; б)

► а) Находим корни уравнения

или Получим ,

Пользуясь формулой (7), запишем:

.

б) Находим корни уравнения ,

Пользуясь формулой (7), запишем:

.

2.5. Теорема Виета: если , то

Если то

2.6. График квадратной функции

График функции есть парабола; осью симметрии графика является прямая . При ветви параболы направлены вверх, а при -- вниз.

При построении графика квадратного трёхчлена полезно придерживаться следующего плана:

1. Определить координаты вершины параболы

и .

2. Определить точку пересечения параболы с осью абсцисс, т.е. корни уравнения .

3. Определить точку пересечения с осью ординат, при , .

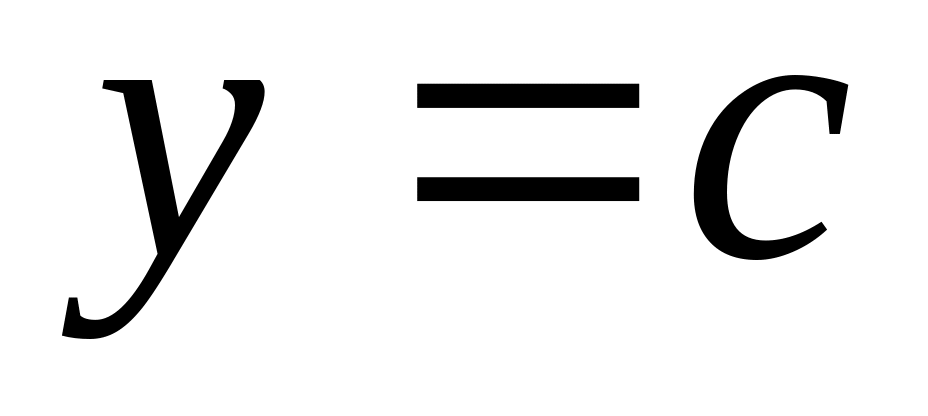Пример. Построить график функции .

►1) Вершина параболы имеет координаты ,

2) Точки пересечения с осью :

3. Точка пересечения с осью ординат, при , .

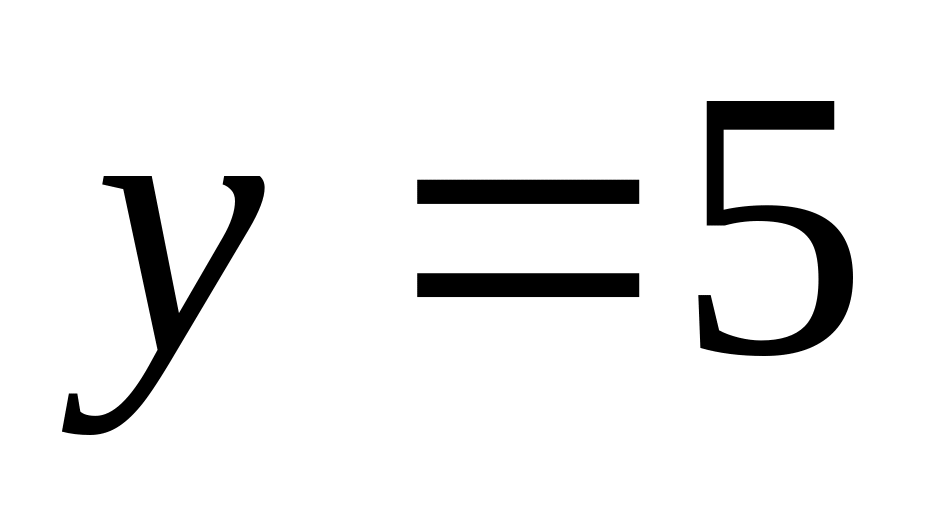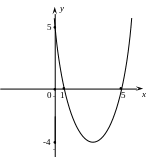
Рисунок 1