- •Лабораторная работа 1 Начало работы с текстовым процессором Word 2007
- •Создание и сохранение документа Word
- •Использование справочной системы Word
- •Настройка панели быстрого доступа
- •Задание параметров страницы
- •Изучение пункта меню Главная
- •Дополнительные возможности работы со шрифтами
- •Лабораторная работа 2 Оформление документов в Word 2007
- •Создание многоуровневых списков
- •Задание Границ и заливки для оформления документов
- •Редактирование документа Word
- •Оформление газетного стиля
- •Задание абзацных отступов
- •Лабораторная работа 3 Оформление многостраничных документов
- •Копирование и редактирование в Word
- •Работа со стилями
- •Вставка и изменение колонтитулов
- •Вставка и редактирование символов и формул
- •Лабораторная работа 4 Элементы оформления документов в Word 2007
- •Вставка таблиц в документ Word
- •Форматирование таблиц
- •Вставка рисованных объектов
- •Вставка рисунков, созданных на основе библиотеки Фигуры
- •Лабораторная работа 5 Элементы сложного оформления документов в Word 2007
- •Формирование оглавления в документах Word
- •Вставка сносок и перекрестных ссылок
- •Вставка названий и формирование списка иллюстраций
- •Элементы рецензирования документов
- •Управление видом документа вкладка Вид
- •Печать документов
- •Обтекание рисунка текстом
- •Расположение рисунка под текстом
- •Газетный стиль текста
- •Шрифты Word
- •Приложение 3 многоуровневый список
- •Многоуровневый список
- •Приложение 4 Формулы в word
- •Приложение 5 Фрагменты текста
- •Аппроксимация первой и второй производных через конечные разности
- •Численное вычисление значений определенного интеграла
- •Постановка задачи
- •Метод прямоугольников
- •Метод трапеций
- •Учебное издание Мокрова Наталия Владиславовна текстовый процессор microsoft office word 2007
Выделение текста всего документа выполняется с помощью команды
Главная \ Редактирование \ Выделить \ Выделить все.
Приложение 4 Формулы в word
Вар. 1.
|
Вар. 2.
|
Вар. 3.
|
Вар. 4.
|
Вар 5.
|
Приложение 5 Фрагменты текста
Вариант 1
Аппроксимация первой и второй производных через конечные разности
Вспомним определение первой производной. Если f (x) – функция одной переменной и x0 [a, b], то функцию f (x) можно записать
![]() ,
(1)
,
(1)
где x0 – фиксированная точка.
Геометрическая интерпретация показана на рис. 1. Пусть на графике функции f заданы фиксированная точка P0 [x0, f (x0)] и подвижная точка P [x, f(x)], и секущая, проведенная через эти точки, образует угол с положительным направлением оси x.
![]() .
(2)
.
(2)
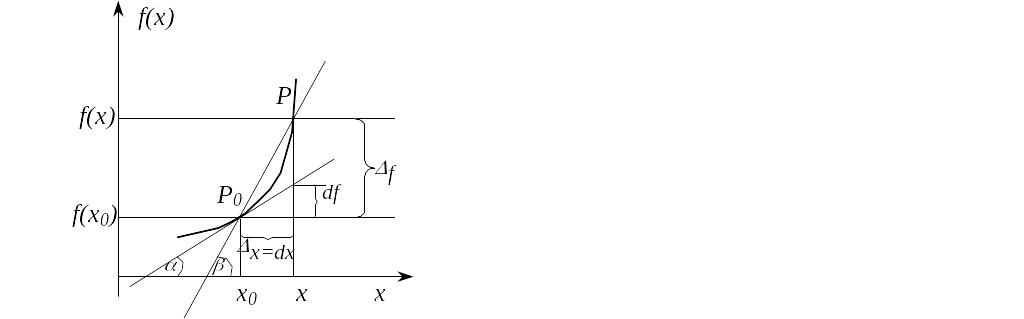
Рис. 1. Геометрическая интерпретация первой производной
Разностное отношение функции f в точке x0 равно угловому коэффициенту секущей, проведенной через точки P и P0.
Функция f называется дифференцируемой в точке x0[a,b], если существует предел разностного отношения функции в точке x0:
![]() .
(3)
.
(3)
Предел (3) называется производной функции f в точке x0 и обозначается
![]() .
(4)
.
(4)
Производная функции f в точке x0 – это тангенс угла наклона касательной к графику функции f в точке P0[x0, f(x0)] (рис. 1)
![]() .
(5)
.
(5)
Простейшая формула численного (приближенного) дифференцирования для непрерывной функции в точке x0 через конечные разности имеет вид
![]() (6)
(6)
или
![]() ,
,
где x=x1 – x0 или в общем виде x=xi – xi-1 – шаг дифференцирования, величина которого должна быть достаточно малой.
Если
производная функции f
/ (4) дифференцируема в точке x0,
то
![]() называется
второй производной
функции f
в точке x0
и обозначается одним из приведенных
способов
называется
второй производной
функции f
в точке x0
и обозначается одним из приведенных
способов
![]() .
(7)
.
(7)
Формула численного нахождения второй производной
![]() (8)
(8)
При подстановке в (8) выражения для нахождения первой производной получим
![]() (9)
(9)
или
![]() .
.
При
численном дифференцировании исходят
из того, что функция
f (x)
задана конечной последовательностью
пар значений (xi ,
fi)
без помехи, и приближенные значения
величин
![]() и
и
![]() находят по формулам (6) и (9).
находят по формулам (6) и (9).
Вариант 2
Численное вычисление значений определенного интеграла
Под определенным интегралом функции f (x) на отрезке [a, b] чаще всего понимают площадь криволинейной фигуры под графиком функции f (x) (рис. 1). Предполагается, что отрезок от a до b разбит на множество маленьких интервалов величиной h, и вычислены площади i-х столбцов Si = f (xi). h, тогда можно с заданной точностью определить значение площади криволинейной трапеции, ограниченной графиком функции f (x) и равной сумме площадей элементарных интервалов.
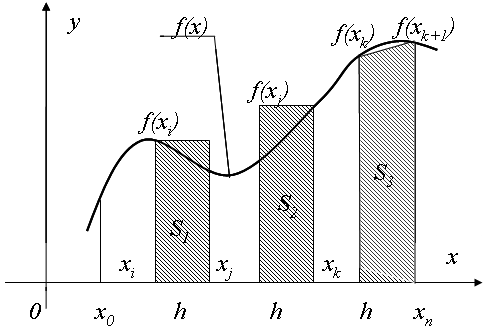
Рис. 1. Геометрическая интерпретация определенного интеграла
Для вычисления определенного интеграла непрерывной функции f (x) на отрезке [a, b] применяют формулу Ньютона-Лейбница
![]() ,
(1)
,
(1)
где F(a), F(b) – первообразные функции от подынтегральной функции F(x) = f `(x). Однако использовать формулу (1) в большинстве случаев невозможно. Для многих функций f (x) первообразную F(x) сложно определить. Кроме того, функция f (x) может быть задана не аналитически, а таблично. В этом случае используют приближенные формулы для вычисления интеграла.
Численное интегрирование широко применяется в практических расчетах, учитывая простую реализацию на компьютере и разнообразие реальных функциональных зависимостей, не описываемых элементарными функциями, заданными таблично и др.
Существует несколько методов численного интегрирования. Наиболее известные из них методы прямоугольников (4), метод трапеции (6) и метод Симпсона. Сформулируем общую постановку задачи.
Постановка задачи
Пусть требуется вычислить
![]() (2)
(2)
на отрезке [a, b], если известно, что a и b – нижний и верхний пределы интегрирования, а функция f (x) непрерывна на интервале [a, b].
Метод прямоугольников
Согласно общему подходу численного интегрирования интервал [a, b] разделяют на n участков длиной
![]() .
(3)
.
(3)
На каждом участке [xi, xi+1] заменяют подынтегральную функцию горизонтальной прямой и определяют площадь элементарного прямоугольника Si = f (xi).
Обобщенная формула для приближенного вычисления определенного интеграла методом левых прямоугольников имеет вид
![]() .
(4)
.
(4)
Замена реальной функции f (x) уравнением прямой на участках интегрирования вносит определенную погрешность в вычисление интеграла. Погрешность будет уменьшаться при увеличении количества разбиений интервала за счет более точной аппроксимации подынтегральной функции. Очевидно, что при
![]() .
(5)
.
(5)
Погрешность вычисления определенного интеграла методом
прямоугольников по формуле (4) пропорциональна шагу интегрирования h.
Метод трапеций
Более точно вычислить определенный интеграл можно с помощью метода трапеций. Подынтегральная функция f (x) разбивается на n равных участков, которые заменяются прямыми, соединяющими точки со значениями функции на границах каждого элементарного участка аппроксимации f (xk), f (xk+1). Сумма площадей образованных таким образом трапеций (рис. 1) при том же значении n точнее приближает значение интеграла к истинному, по сравнению с методами прямоугольников.
Интегральная сумма метода трапеции может быть рассчитана по одной из равносильных формул:
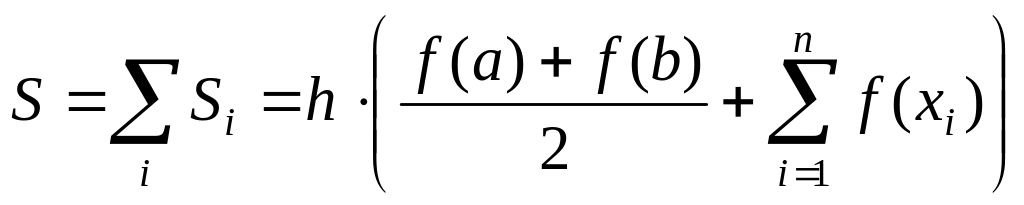 (6)
(6)
![]() .
.
Погрешность метода трапеций (6) пропорциональна h2.
Приложение 6
Блок-схемы в Word
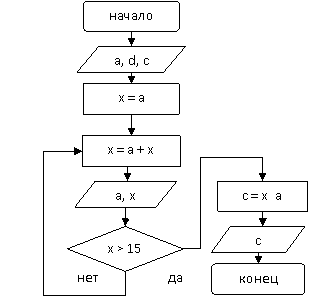
Вар. 1.
|
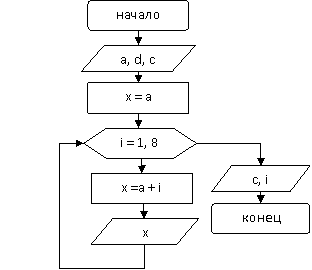
Вар. 3.
|
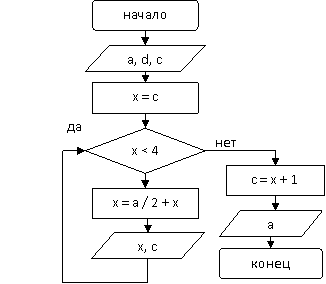
Вар. 2.
|
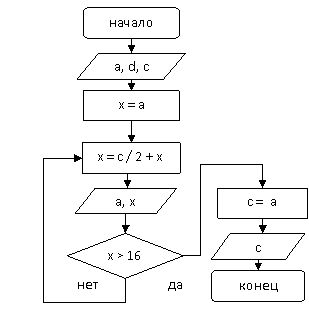
Вар. 4.
|
Приложение 7
Примерный вариант
Контрольной работы Word
Исходный текст с помощью MS Word отформатируйте в соответствии с приведенным заданием.
Оформите первый лист документа как титульный, на котором введите название документа (размер шрифта – 35 пт., интервал – разреженный на 2,5 пт.). Добавьте объект WordArt –
 (подобрать палитру, поместить
за текстом).
(подобрать палитру, поместить
за текстом).
Для текстовой части документа установите стиль оформления: шрифт – Arial; 14 пт.; интервал между символами обычный; межстрочный интервал множитель 1,4; выравнивание по ширине страницы, автоматическая расстановка переносов.
Выделите и озаглавьте разделы документа. Установите красную строку с отступом 1,25 см.
Для заданных слов во всем тексте установите шрифт жирный, разреженный на 2 пт. (использовать правка/замена).
Выделенный раздел оформите многоуровневым списком.
Создайте верхние колонтитулы на всех страницах документа, за исключением первой страницы (название документа). На титульном листе создайте нижний колонтитул, содержащий вашу фамилию.
Часть документа оформите в три колонки.
Одну страницу расположите на альбомных листах.
Вставьте в документ рисунки, расположив их в тексте. Сделайте надписи.
Установите сквозную нумерацию страниц, начиная со второй. Подготовьте документ к печати. Установите следующие параметры страницы: верхние и нижние поля – 2 см., левое поле – 3 см., правое – 1,5 см., отступ от колонтитула – 1 см.
Оформите и отредактируйте таблицу согласно заданию.
Вставьте в документ заданные нумерованные формулы.
Составьте автоматически обновляемое оглавление полученного текста.
Составьте список иллюстраций.
Учебное издание Мокрова Наталия Владиславовна текстовый процессор microsoft office word 2007
Подписано в печать 15.11.2011. Формат бум. 60 x 84 1/16.
Объем 3,02 усл. п. л. Уч-изд. л. 3,25. Тираж 100 экз. Зак. 1/2012