Билет №12 Равномерная сходимость функциональных последовательностей и рядов.

Рассмотрим последовательность функций

Говорят, что последовательность (1) сходится на множестве E равномерно к функции , если

при

При этом пишут

.

Теорема 1 (критерий Коши равномерной сходимости последовательности).

Последовательность , сходится на E равномерно тогда и только тогда, когда выполняется условие Коши:

.

Доказательство.

Необходимость. Пусть . Тогда

при

Отсюда следует, что ,

Достаточность. Пусть выполнено условие Коши. Тогда при каждом фиксированном выполнено условие

.(2)

В силу критерия Коши сходимости числовой последовательности {f_n(x)} сходится для . Обозначим предел числовой последовательности {f_n(x)} через f(x). Покажем, что . Перейдем для этого в оценке (2) к пределу при . Получим, что

.

Переходя в последнем неравенстве к верхней грани по , видим что по определению 2.

Теорема 1.

Пусть последовательность комплеснозначных фукций равномерно сходится на E к функции f. т.е. . Если все функции f_n непрерывны в точке x⁽⁰⁾ по множеству E.

Доказательство. Пусть . Тогда

.

Тогда при

.

В силу непревности функции в точке x⁽⁰⁾ по множеству E

.

Отсюда и из предыдущего неравенства следует, что

Следовательно, функция f непрерывна в точке x⁽⁰⁾ по множеству E.

Теорема 2.

Пусть функции f_n непрерывны на отрезке при всех и при .

Тогда

при .

Доказательство. Функция по теореме 1 непрерывна на отрезке [a,b] при всех и, следовательно интегрируема на [a,b]. Пусть . Тогда в силу равномерной сходимости {f_n} к функции f

.

Следовательно для всех

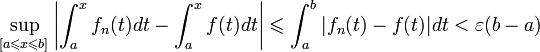
откуда и следует утверждение теоремы.

Теорема 3

Пусть последовательность {f_n} непрерывно дифференцируемых на отрезке [a,b] функций сходится в точке , а, последовательность производных {f'_n} равномерно сходится на [a,b] к некоторой функции φ.

Тогда последовательность {f_n} равномерно сходится на [a,b] к некоторой функции непрерывно дифференцируемой на [a,b] функции f и f' = φ, так что на [a,b].

Доказательство. По теореме 1 функция φ непрерывна на [a,b]. В силу теоремы 2 и формулы Ньютона-Лейбница получаем, что

.

Числовую сходящуюся последовтельность {f_n(c)} можно считать, очевидн, функциональной последовательностью, равномерно сходящейся на [a,b]. Тогда последовательность {f_n} равномерно сходиться на [a,b] к некоторой функции f.

Переходя в левой части последней формулы к пределу при , получаем, что

.

Правая часть этого равенства является дифференцируемой функцией. Следовательно таковой является и левая часть, а значит и функция f. Дифференцируя равенство получаем, что . Теорема доказана.

Билет №13 Степенные ряды.

Функциональный ряд

где a_n и z₀ - комплексные числа, а z - комплексная переменная, называется степенным рядом.

Радиусом сходимости степенного ряда называется число или :

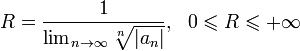
Пусть R > 0 - радиус сходимости ряда

a_k - вещественные числа.

Тогда при | x − x₀ | < R f имеет производные всех порядков, которые находятся почленным дифференцированием;

Доказательство.

Докажем утверждение, что степенные ряды, полученные почленным дифференцированием или почленным интегрированием, имеют тот же радиус сходимости R.

Радиусы сходимости рядов и совпадают.

Доказательство.Пусть радиусы сходимости указанных рядов соответственно R и R'. Очевидно, что ряд сходится там же, где , и, следовательно, имеет тот же радиус сходимости R'. В силу

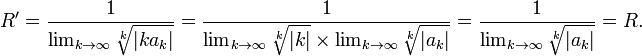
Доказано.

Если функция определена в некоторой окрестности точки и имеет в точке x₀ производные всех порядков (т.е. является бесконечно дифференцируемой в точке x₀), то степенной ряд

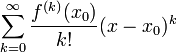
называется рядом Тейлора функции f в точке x₀.