14. Решетки. Дистрибутивные решетки. Критерий дистрибутивности.

Элемент называется точной верхней гранью (супремумом) множества В (обозначается supB), если а – наименьшая из всех верхних граней множества В. Элемент называется точной нижней гранью (инфимумом) множества В (обозначается infB), если а – наибольшая из всех нижних граней множества В.

Решеткой называется ЧУМ α=<A,≤>, в котором каждая пара элементов имеет супремум и инфимум. Для заданных элементов элемент inf{x,y} называется пересечением элементов x и y ( ), а sup{x,y} называется объединением элементов x и y ( ). Заметим, что тогда и . Наибольший (наименьший) элемент решетки, если он существует, называется нулем (единицей). В конечных решетках всегда есть нуль и единица.

Определим решетку подсистем системы β=<B,∑>, содержащих непустое множество . Рассмотрим множество и зададим на нем частичный порядок ≤ по следующему правилу: . Пара <L(β),≤> образует решетку подсистем. В этой решетке для любых систем α₁=<A₁,∑>, α₂=<A₂,∑> из L(β) пересечение есть подсистема , а объединение - подсистема, порожденная множеством .

Пусть α=<A,∑> - алгебра, Conα={θ | θ – конгруэнция на α}. На множестве конгруэнций Conα зададим отношение ≤ по следующему правилу: θ₁≤θ₂ <=> для любых элементов из условия aθ₁b вытекает aθ₂b. Это означает, что каждый θ₂-класс состоит из θ₁-классов. Система <Conα,≤> образует решетку конгруэнций. В этой решетке: для любых тогда и только тогда , когда aθ₁b и aθ₂b; для любых тогда и только тогда , когда существуют такие , что c₁=a, c_n=b и справедливо c_iθ₁c_i+1 или c_iθ₂c_i+1 для любого i=1,…, n-1. Решетка конгруэнций имеет нулевую конгруэнцию и единичную конгруэнцию 1_A=A².

Р ешетка α=<A,≤> называется дистрибутивной, если она подчиняется дистрибутивным законам для всех .

Недистрибутивные решетки:

Критерий дистрибутивности: Решетка α=<A,≤> дистрибутивна тогда и только тогда, когда она не имеет подрешеток, изоморфных М₃ или Р₅.

15. Булевы алгебры. Теорема Стоуна. Принцип двойственности для булевых алгебр.

Дистрибутивная решетка α=<A,≤> называется булевой алгеброй, если α имеет нуль0, единицу 1, 0≠1 и для любого элемента х из А найдется элемент (дополнение х) такой, что , .

Утверждение: Если α=<A,≤> - булева алгебра, то для любого элемента х дополнение единственно.

Доказательство: Предположим, что элемент х имеет два дополнения y и z, т.е. . По закону дистрибутивности получим, что элементы также являются дополнениями х, т.е. . При этом из y≠z следует, что . Отсюда получаем, что подрешетка решетки α с носителем образует решетку Р₅, что противоречит дистрибутивности решетки α. Наше допущение неверно.

Свойства булевой алгебры:

1. Ассоциативность:

2. Коммутативность:

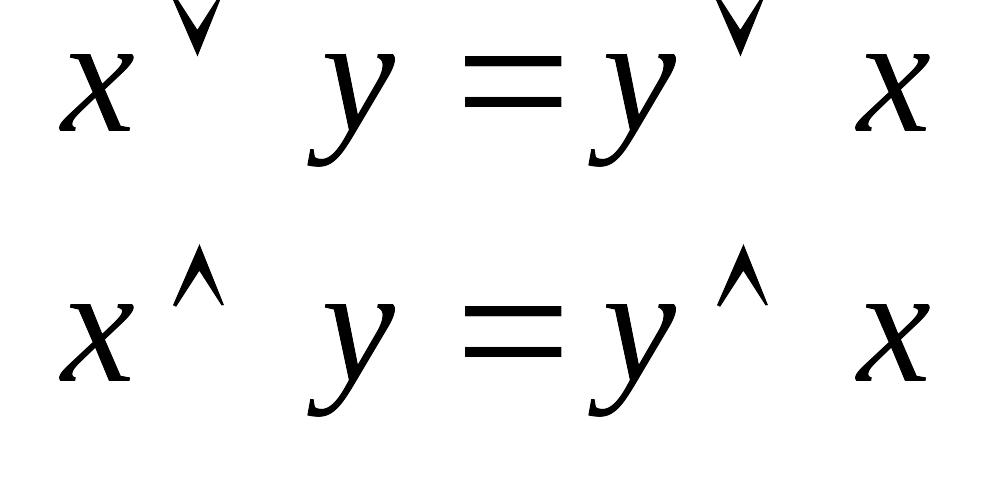
3. Идемпотентность:

4. Дистрибутивность:

5. Поглощение:

6. Законы де Моргана:

7. Законы нуля и единицы: 0=ø, 1=U

8. Закон двойного отрицания:

Теорема Стоуна: Любая конечная булева алгебра изоморфна некоторой алгебре Кантора ( )

Следствие: Любые две булевы алгебры, имеющие одинаковое число элементов, изоморфны. Число элементов конечной булевой алгебры равно 2ⁿ для некоторого .

Таким образом, конечная булева алгебра определяется однозначно с точностью до изоморфизма числом своих элементов.

Принцип двойственности для булевых алгебр: если в справедливом утверждении о булевых алгебрах, касающемся отношения ≤ и операций , всюду заменить на соответственно, то получится также справедливое утверждение, называемое двойственным к исходному.