
- •Множества. Основные операции над множествами и их свойства. Диаграммы Венна. Декартово произведение множеств.
- •Отношения и бинарные отношения, область определения, область значения, обратные отношения. Произведение отношений.
- •Функции. Инъекции, сюръекции, биекции. Понятие последовательности.
- •Множество натуральных чисел. Два подхода к определению множества натуральных чисел. Аксиомы Дедекинда-Пеано. Принцип математической индукции.
- •Понятие мощности множества. Сравнение мощностей. Теорема Кантора-Берштейна. Операции над кардинальными числами.
- •Конечные, счетные, континуальные множества. Мощность булеана.
- •Матрицы бинарных отношений и их свойства. Специальные бинарные отношения.
- •Отношения эквивалентности и разбиения. Фактор-множества. Матрица отношения эквивалентности.
- •Отношения порядка. Максимальные и минимальные, наибольший и наименьший элементы частично упорядоченного множества. Диаграммы Хассе. Линейно и вполне упорядоченные множества.
- •Алгебраические системы: определение и примеры. Понятие полугруппы, моноида, группы; задание с помощью таблицы Кэли.
- •Морфизмы алгебраических систем.
- •Подсистемы. Термы сигнатуры ∑. Подсистема, порожденная множеством, ее структура.
- •Конгруэнции, фактор-алгебры, теорема о гомоморфизме.
- •17.Многообразия. Теорема Биркгофа.
- •Решетки. Дистрибутивные решетки. Критерий дистрибутивности.
- •Булевы алгебры. Теорема Стоуна. Принцип двойственности для булевых алгебр.
- •Булево кольцо.
- •18. Алгебры отношений. Реляционные алгебры.
- •27. Виды и способы задания графов.
- •28. Подграфы и части графа. Операции над графами. N-Мерные кубы.
- •Объединение: .
- •29. Маршруты, циклы, цепи. Достижимость и связность (матрицы достижимости, контрдостижимости, связности).
- •30. Расстояние в графах. Центральные и периферийные вершины.
- •31. Взвешенное расстояние. Алгоритм Форда-Беллмана.
- •32. Степени вершин. Эйлеровы графы, циклы, цепи. Алгоритм построения эйлерова цикла.
- •33. Гамильтоновы графы. Постановка задачи коммивояжера.
- •34. Деревья, леса. Остовы графов. Цикломатическое число, коранг. Алгоритм построения остова минимального веса. Обходы графов по глубине и ширине.
- •35. Упорядоченные и бинарные деревья. Соответствия между ними.
- •36. Фундаментальные циклы, разрезы. Матрицы фундаментальных циклов, разрезов.
- •37. Раскраска графов. Планарные графы.
- •38. Формулы алгебры логики, их таблицы истинности.
- •39. Булевы функции, способы их задания. Представления булевых функций формулами.
- •40. Эквивалентность формул.
- •41. Двухэлементная булева алгебра. Алгебра булевых функций. Фактор-алгебра алгебры формул.
- •42. Дизъюнктивные и конъюнктивные нормальные формы. Алгоритм приведения формулы к днф и кнф.
- •43. Теорема Шеннона. Теорема о функциональной полноте. Способы построения сднф и скнф.
- •44. Импликанты, простые импликанты. Сокращенные, тупиковые, минимальные нормальные формы. Алгоритм Квайна построения мднф.
- •45. Карты Карно. Построение мднф с помощью карт Карно.
- •46. Принцип двойственности. Самодвойственные функции.
- •47. Теорема Жегалкина. Способы построения полиномов Жегалкина. Линейные функции.
- •48. Классы Поста. Полные системы булевых функций. Теорема Поста. Базисы.
- •49. Логические сети. Реализация булевых функций контактными схемами и схемами из функциональных элементов.
Функции. Инъекции, сюръекции, биекции. Понятие последовательности.
Отношение
![]() называется функцией
или отображением
из множества А в множество В, если
называется функцией
или отображением
из множества А в множество В, если
![]() и из (x,y1)
є f,
(x,y2)
є f
следует y1=y2.
Если вместо
и из (x,y1)
є f,
(x,y2)
є f
следует y1=y2.
Если вместо
![]() выполняется
выполняется
![]() ,
то f
называется частичной
функцией.
Функция f
из А в В обозначается через
,
то f
называется частичной
функцией.
Функция f
из А в В обозначается через
![]() или
или
![]() .
Если (x,y)
є f,
то пишем y=f(x)
или
.
Если (x,y)
є f,
то пишем y=f(x)
или
![]() .
Функция
.
Функция
![]() называется разнозначной
инъективной (инъекцией) или 1-1 функцией
если из условия, что
называется разнозначной
инъективной (инъекцией) или 1-1 функцией
если из условия, что
![]() выполняется х1≠х2,
следует y1≠y2.
Функция
выполняется х1≠х2,
следует y1≠y2.
Функция
![]() называется функцией из А на В или
сюръекцией, если
называется функцией из А на В или
сюръекцией, если
![]() .
Функция
.
Функция
![]() называется взаимно однозначным
соответствием между множествами А и В
или биекцией, если она инъективна и
сюръективна одновременно.
называется взаимно однозначным
соответствием между множествами А и В
или биекцией, если она инъективна и
сюръективна одновременно.
Биекция
![]() называется подстановкой.
называется подстановкой.
Утверждения:
Если
 ,
,
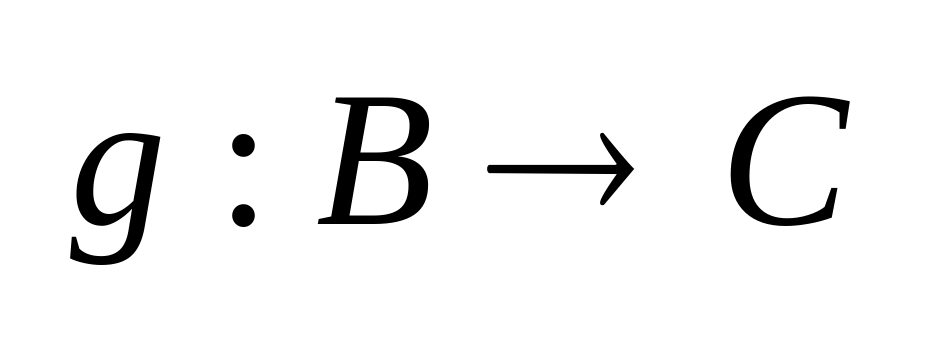 ,
то
,
то

Если
 ,
то
,
то

Если f и g - инъекции, то f•g – инъекция.
Доказательство: Предположим противное, т.е. найдутся элементы x1, x2, y такие, что х1≠х2, (x1,y) є f•g и (x2,y) є f•g, т.е. g(f(x1))=y=g(f(x2)). В силу разнозначности f имеем f(x1)≠f(x2). Отсюда в силу разнозначности g получаем g(f(x1))≠g(f(x2)), а это противоречит предположению.
Если f,g – сюръекции, то f•g – сюръекция
Доказательство: Нужно доказать, что для любого с существует а такое, что f•g(a)=c. Т.к. g – сюръекция, то существует b, для которого g(b)=c, а т.к. f – сюръекция, то для любого b существует а такое, что f(a)=b. Тогда f•g(a)=g(f(a))=c
Если f и g – биекции, то f•g – биекция
Если , то

Функция
![]() называется последовательностью. Её
можно представить в виде f(0)=b0,
f(1)=b1,…,
f(n)=bn.
называется последовательностью. Её
можно представить в виде f(0)=b0,
f(1)=b1,…,
f(n)=bn.
Множество натуральных чисел. Два подхода к определению множества натуральных чисел. Аксиомы Дедекинда-Пеано. Принцип математической индукции.
Два подхода к определению множества натуральных чисел:
Конструктивный.
Позволяет представить натуральные числа в виде объектов, построенных из пустого множества.
Положим по определению
![]()
![]()
![]()
![]() .
Множества 0, 1, 2,… называются натуральными
числами.
Объединение этих чисел N={0,
1, 2,…, n,…}
называется множеством
натуральных чисел.
.
Множества 0, 1, 2,… называются натуральными
числами.
Объединение этих чисел N={0,
1, 2,…, n,…}
называется множеством
натуральных чисел.
Замечание: АВ – множество всех функций из В в А. Если В=n={0,1,2…,n-1}, A=2={0,1}, то АВ=2n.
Аксиоматический подход.
Рассмотрим аксиоматику Дедекинда Пеано:
Пусть имеется некоторое множество N, в котором выбран элемент 0 и функция, которая элементу n из N ставит в соответствие элемент n’ из N, называемый непосредственно следующим (элемент n’ играет роль числа n+1).
Множество N называется множеством натуральных чисел, если система <N,0,’> удовлетворяет аксиомам:
- для любого m≠0 найдется n из N такой, что n’=m.
- для любых m,n из N, если m’=n’, то m=n.
- n’≠0 для любого n из N.
- на множестве N выполняется аксиома математической индукции.
Принцип (аксиома) математической индукции:
Для любого свойства Р (унарного отношения на множестве N), если Р выполняется на элементе 0 (т.е. 0 обладает свойством Р), и для любого n из N из выполнимости Р на элементе n следует выполнимость Р на элементе n’, то свойство Р выполняется на любом элементе n из N.
![]() или
или
![]() или
или
![]()
Иногда удается установить только выполнение Р(к) для некоторого к>0 и свойство Р(n)=>Р(n+1) для всех n≥к:
![]()
Принцип полной индукции:
Если для всякого n из N из предположения, что P(k) верно при любом натуральном k<n, следует, что P(k) верно также при k=n, то P(n) верно при любом натуральном n:
![]()
