Предпосылки регрессионного анализа

1. Для каждого наблюдения распределение остаточной компоненты не зависит от значений предикторов.

2. Математическое ожидание остаточной компоненты во всяком наблюдении равно нулю:

.

Такое требование естественно полагать выполненным, поскольку функциональная компонента регрессионной модели должна учитывать любую систематическую тенденцию в изменении значений переменной Y.

3. Дисперсия остаточной компоненты одинакова для всех наблюдений:

.

4. Для любых двух наблюдений остаточные компоненты не коррелированы:

.

5. Для каждого наблюдения распределение вероятностей остаточной компоненты подчинено закону Гаусса.

Данное допущение часто основывается на центральной предельной теореме, состоящей в том, что если случайная величина обусловлена взаимодействием большого числа других случайных величин, причем ни одна из них не оказывает доминирующего влияния на общий результат, то распределение результирующей случайной величины близко к нормальному.

Из условий Гаусса - Маркова непосредственно следует, что:

• для i-го наблюдения критериальная переменная Y подчинена нормальному закону распределения вероятностей с математическим ожиданием 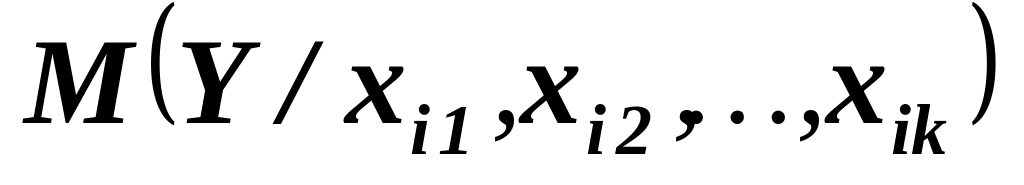, являющимся функцией только предикторов, и дисперсией 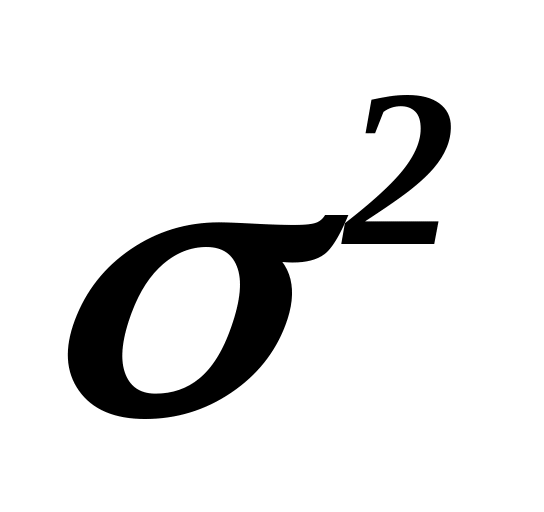, не зависящей от реализаций случайного вектора (X₁, X₂,…, X_k);

• для произвольных двух наблюдений остаточные компоненты стохастически не независимы.

Замечание

При проведении расчетов оценок параметров множественной линейной модели регрессионного анализа с помощью МНК рекомендуется, чтобы n - число наблюдений - превосходило k+1 - число параметров модели - не менее чем в три раза.

Уравнение множественной линейной регрессии

Определяя на основании модельного уравнения (1) условное математическое ожидание критериальной переменной Y в предположении, что предикторы X₁, X₂, …, X_k приняли соответственно некоторые конкретные значения x₁, x₂,…, x_k, принимая во внимание, что в этом случае β₀+β₁x₁+β₂x₂+…+β_jx_j+…+β_kx_k есть константа, учитывая также, что согласно второй предпосылке регрессионного анализа M( ) равно нулю, получаем уравнение регрессии:

M(Y/x1,x2,…,xk)=β0+β1x1+β2x2+…+βjxj+…+βkxk

(5)

Следовательно, функциональная составляющая исходной регрессионной модели представляет собой функцию регрессии.

Конкретизируя на основании имеющихся статистических данных n выборок: (y_i, x_i1, x_i2,…, x_ij,…, x_ik) вид уравнения регрессии (5) для каждого произведенного наблюдения, приходим к системе n равенств:

,

(6)

где символом обозначено M(Y/x_i1,x_i2,…,x_ik) - условное математическое ожидание переменной Y в i-ом наблюдении.

В матричной форме система уравнений (6) приобретает вид

,

(7)

здесь - вектор-столбец размерности n с элементами .

Итак,

.

(8)

Из соотношения (8) вытекает представление вектора остатков:

.

(9)

Оценка параметров модели множественной линейной регрессии по методу наименьших квадратов

Согласно этому методу в качестве оценки неизвестного вектора принимают тот вектор , который минимизирует квадрат длины вектора - остаточную сумму квадратов отклонений фактических значений критериальной переменной Y от соответствующих расчетных значений, найденных на основе уравнения регрессии Y на (X₁, X₂,…, X_k):

,

т.е. искомый вектор должен удовлетворять требованию

.

Необходимые и достаточные условия минимума квадратичной формы Q_ост, рассматриваемой как функция аргументов β₀, β₁, β₂,…, β_j,…, β_k, известны из математического анализа:

.

Осуществляя дифференцирование функции

отдельно по каждому из параметров β₀, β₁, β₂,…, β_j,…, β_k, и приравнивая производные нулю, получаем k+1 соотношение для b₀, b₁, b₂,…, b_j,…, b_k - МНК-оценок искомых параметров модели:

.

(10)

Данная система в матричной форме записываются так:

.

(11)

где Х^Т – матрица, транспонированная к матрице X.

Если - невырожденная матрица, то умножая слева обе части уравнения (11) на обратную матрицу , находим матричное выражение, определяющее МНК-оценку параметров модели множественной линейной регрессии как вектор-функцию выборочных данных:

.

(12)
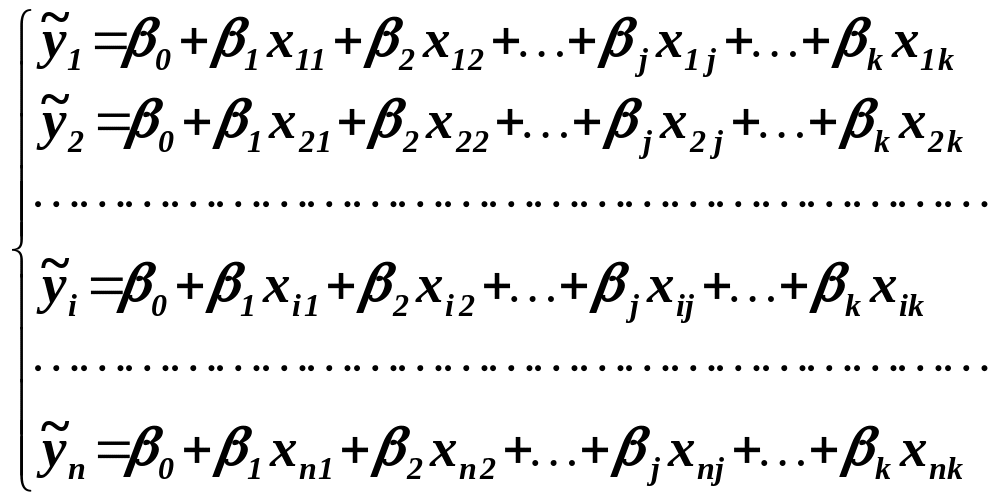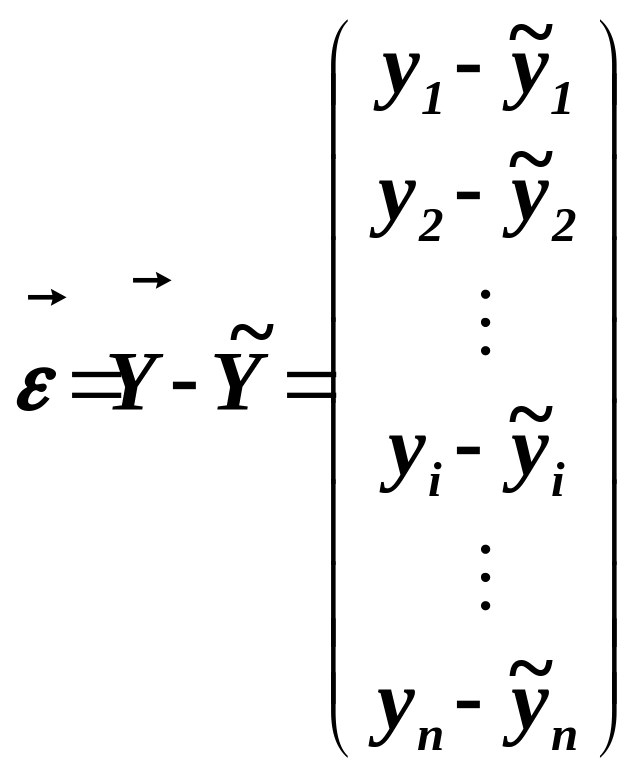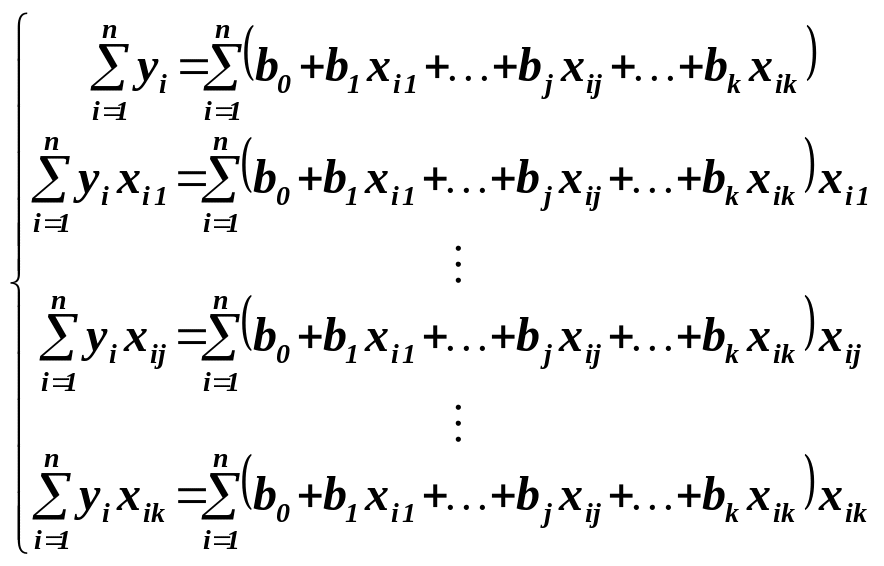