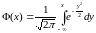- •Екзаменаційний білет № 11
- •Формула Тейлора функції однієї змінної .
- •11.2 Перевiрка статистичних гiпотез. КритерiїКолмогорова та Пiрсона.
- •Екзаменаційний білет № 12
- •12.2Випадкове середнє та дисперсія. Емпiричнафункцiярозподiлу.
- •Екзаменаційний білет № 13
- •Теорема існування та єдиностi розв'язку задачi Кошiдиференцiальногорiвняння першого порядку.
- •Поняття випадкового процесу. Вiнерiвський та Пуасонiвський процеси.
- •Екзаменаційний білет № 14
- •14.1. Лiнiйнiоднорiднiдиференцiальнiрiвняння n-го порядку iз сталими коефiцiєнтами. Побудова загального розв'язку.
- •14.2. Центральна гранична теорема для однаково розподiлених незалежних випадкових величин.
- •Екзаменаційний білет № 15
- •15.1Системи лiнiйнихдиференцiальнихрiвнянь з сталими коефiцiєнтами. Знаходження загального розв'язку однорiдних систем.
- •Системилінійниходноріднихдиференціальнихрівнянь з сталимикоефіцієнтами.
- •4.3.1. Розв’язування систем однорідних рівнянь з сталими коефіцієнтами методом Ейлера.
- •Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом
- •15.2Основнi типи дискретних та неперервних розподiлiв.
- •Екзаменаційний білет № 16
- •Властивості розв’язків лінійних неоднорідних систем
- •Побудова частинного розв’язку неоднорідної системи методом варіації довільних сталих
- •Формула Коші
- •НерiвнiстьЧебишева. Закон великих чисел.
- •Екзаменаційний білет № 17
- •17.1Теорiя стiйкостi. Стiйкiстьлiнiйнихстацiонарних систем. Критерій Гурвiца. Теореми Ляпунова.
- •Фазовий портрет лінійноїсистеми на площині
- •17.2Випадковi величини. Властивостiфункцiйрозподiлу.
- •Екзаменаційний білет № 18
- •18.1Динамічні системи. Означення та класифікація динамічних систем за Калманом.
- •18.2Аксiоматичне означення ймовiрностей. Формула повної ймовiрностi та формула Байеса.
- •Екзаменаційний білет № 19
- •Задача однофакторного дисперсійного аналізу та її розв’язання.
- •19.2Первинні оператори. Оператор присвоєння. Структурні оператори (складені, умовні, циклічні). Оператор вводу-виводу.
- •Екзаменаційний білет № 20
- •Градiєнт, дивiргенцiя I вихор векторного поля.
- •20.2 Слабко-ефективні альтернативи. Теорема Гермейєра.
Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом
Досить
універсальним методом розв’язку
лінійних однорідних систем з сталими
коефіцієнтами є матричний метод. Він
полягає в наступному. Розглядається
лінійна система з сталими коефіцієнтами,
що записана у векторно-матричному
вигляді
 .
Робиться невироджене перетворення
.
Робиться невироджене перетворення
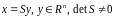 ,
де вектор
,
де вектор
 - нова невідома векторна функція. Тоді
рівняння прийме вигляд
- нова невідома векторна функція. Тоді
рівняння прийме вигляд
 або
або
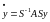 .
Для довільної матриці
завжди існує неособлива матриця
.
Для довільної матриці
завжди існує неособлива матриця
 ,
що приводить її до жорданової форми,
тобто
,
що приводить її до жорданової форми,
тобто
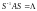 ,
де
,
де
 -
жорданова форма матриці
.
І система диференціальних рівнянь
прийме вигляд
-
жорданова форма матриці
.
І система диференціальних рівнянь
прийме вигляд
 .
Складемо характеристичне рівняння
матриці
:
.
Складемо характеристичне рівняння
матриці
:
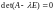 , або
, або
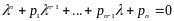 .
Алгебраїчне рівняння
-го
ступеня має
коренів. Розглянемо різні випадки.
.
Алгебраїчне рівняння
-го
ступеня має
коренів. Розглянемо різні випадки.
1.
Нехай
 -
дійсні різні числа. Тоді матриця
має вигляд
-
дійсні різні числа. Тоді матриця
має вигляд
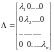 .
І перетворена система диференціальних
рівнянь розпадається на
- незалежних рівнянь
.
І перетворена система диференціальних
рівнянь розпадається на
- незалежних рівнянь
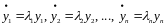 .
.
Розв’язуючи
кожне окремо, отримаємо
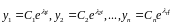 .
Або в матричному вигляді
.
Або в матричному вигляді
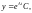 де
де
 .
Звідси розв’язок вихідного рівняння
має вигляд
.
Звідси розв’язок вихідного рівняння
має вигляд
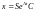 .
Для знаходження матриці
.
Для знаходження матриці
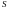 треба розв’язати матричне рівняння
або
треба розв’язати матричне рівняння
або
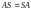 ,
де
- жорданова форма матриці
.
Якщо матрицю
записати у вигляді
,
де
- жорданова форма матриці
.
Якщо матрицю
записати у вигляді
 ,
то для кожного з стовпчиків
,
то для кожного з стовпчиків
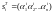 ,
матричне рівняння перетвориться до
,
матричне рівняння перетвориться до
 ,
,
 .
Таким чином, у випадку різних дійсних
власних чисел матриця
являє собою набір
- власних векторів, що відповідають
різним власним числам.
.
Таким чином, у випадку різних дійсних
власних чисел матриця
являє собою набір
- власних векторів, що відповідають
різним власним числам.
2.
Нехай
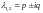 -
комплексний корінь. Тоді відповідна
клітка Жордана має вигляд
-
комплексний корінь. Тоді відповідна
клітка Жордана має вигляд
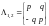 ,
,
а
перетворена система диференціальних
рівнянь
 Неважко
перевірити, що розв’язок отриманої
системи диференціальних рівнянь має
вигляд
Неважко
перевірити, що розв’язок отриманої
системи диференціальних рівнянь має
вигляд
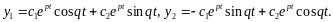
Або
в матричному вигляді
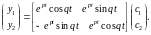 Таким
чином, комплексно-спряженим власним
числам
відповідає
розв’язок
де
Таким
чином, комплексно-спряженим власним
числам
відповідає
розв’язок
де

3.
Нехай
 -
кратний корінь, кратності
-
кратний корінь, кратності
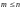 ,
тобто
,
тобто
 і йому відповідають
і йому відповідають
 лінійно незалежних векторів. Тоді клітка
Жордана, що відповідає цьому власному
числу, має вид
лінійно незалежних векторів. Тоді клітка
Жордана, що відповідає цьому власному
числу, має вид

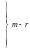
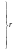
І перетворена підсистема, що відповідає власному числу , розпадається не дві підсистеми
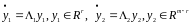 .
.
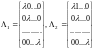 .
Розв’язок першої знаходиться з
використанням зазначеного в першому
пункті підходу. Розглянемо другу
підсистему. Запишемо її в координатному
вигляді
.
Розв’язок першої знаходиться з
використанням зазначеного в першому
пункті підходу. Розглянемо другу
підсистему. Запишемо її в координатному
вигляді
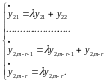 Розв’язок
останнього рівняння цієї підсистеми
має вигляд
Розв’язок
останнього рівняння цієї підсистеми
має вигляд
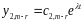 .
.
Підставимо
його в передостаннє рівняння. Одержуємо
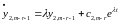 .
Загальний розв’язок лінійного
неоднорідного рівняння має вигляд суми
загального розв’язку однорідного і
частинного розв’язку неоднорідних
рівнянь, тобто
.
Загальний розв’язок лінійного
неоднорідного рівняння має вигляд суми
загального розв’язку однорідного і
частинного розв’язку неоднорідних
рівнянь, тобто
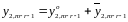 .
Загальний розв’язок однорідного має
вигляд
.
Загальний розв’язок однорідного має
вигляд
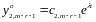 .
.
Частинний
розв’язок неоднорідного шукаємо методом
невизначених коефіцієнтів у вигляді
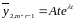 ,
,
де
-
невідома стала. Підставивши в неоднорідне
рівняння, одержимо 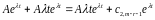 .
.
Звідси
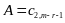 і загальний розв’язок неоднорідного
рівняння має вигляд
і загальний розв’язок неоднорідного
рівняння має вигляд
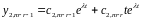 .
.
Піднявшись
ще на один крок нагору одержимо
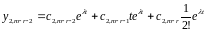 .
Продовжуючи процес далі, маємо
.
Продовжуючи процес далі, маємо
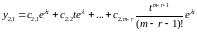 .
Або у векторно - матричному вигляді
.
Або у векторно - матричному вигляді
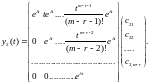 .
Додавши першу підсистему, одержимо
.
Додавши першу підсистему, одержимо
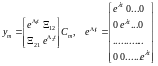 ,
,
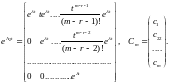
Для
останніх двох випадків матриця
знаходиться як розв’язок матричного
рівняння 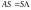 .
.
15.2Основнi типи дискретних та неперервних розподiлiв.
Основні дискретні розподіли.
 -
дискретна множина, скінченна або
злічена.
-
дискретна множина, скінченна або
злічена.
Теорема
Ймовірність
на булеані дискретної множини можна
задати набором
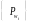 невідємних
чисел, що
невідємних
чисел, що
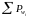 =1,
і ймовірність довільної множини А
дорівнює:
=1,
і ймовірність довільної множини А
дорівнює:
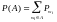 .
.
Цей
набір
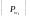 наз.
рядом
розподілу.
наз.
рядом
розподілу.
Бернулівський розподіл з параметром p.
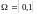 має
2 параметра: p і q
має
2 параметра: p і q
 ,
,
Ряд
розподілу:
 .
.
Цей розподіл описує кількість появ деякої події у одному випробуванні з імовірністю появи р.
Біноміальний розподіл
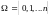

Ряд
розподілу:

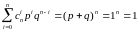
Цей розподіл описує кількість появ деякої події в n незалежних спостереженнях(випробуваннях), коли ймовірність появи події в одному випробуванні дорівнює p.
3. Геометричний розподіл з параметром p.
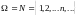
Ряд
розподілу:
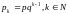
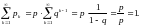
Цей розподіл описує кількість спостережень до першої появи деякої події у n незалежних випробуваннях, коли спостереження незалежні і ймовірність появи цієї події в одному спостереженні дорівнює p.
4.
Пуассонівський
розподіл з параметром
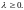 .
.

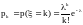
Пуассонівська
в. в. є кількістю появ точкових елементів
у сукупності фіксованого розміру за
середньою кількістю елементів на цю
сукупність (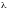 )
)

Неперервні розподіли.
Це
розподіли з неперервною функцією
розподілу F(x). Якщо F(x) - гладка функція,
то
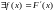 .
Ця функція f(x) - називається щільністю
розподілу.
.
Ця функція f(x) - називається щільністю
розподілу.
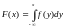
1.
Рівномірний з параметрами
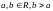
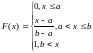
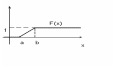
F(x) - кусково-диференційовна
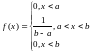

2.
Показниковий з параметром
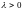
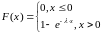
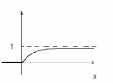
3.
Нормальний з параметрами

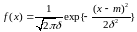 ,
,
Стандартний гауссівський розподіл - N(0,1):
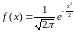 ,
,